входящих в уравнения равновесия, составленные для того, или иного, отдельно взятого тела. Например, линейно независимых уравнений равновесия получается лишь 3, а в них входит 4 или более неизвестных.

На основании лишь этого решаемую задачу относить к категории статически неопределимых не следует - в инженерной практике часты случаи, когда путём объединения систем уравнений равновесия, составленных для различных тел, получают расширенную систему уравнений, в которой число неизвестных оказывается равным числу линейно независимых уравнений.

К

15.33

онструкции, в которых для определения реакций связей приходится объединять уравнения равновесия, составленные для различных тел, называют статически определимыми механическими системамисо сложно сочленёнными частями.

К примеру 15.13

ПРИМЕР 15.13.-Конструкция со сложно сочленёнными частями;

простейший случай

Дано: тела соединены как указано на рис.15.39; кН; м.

Определить реакции в шарнирах А, В и С.

Р

Рисунок 15.39

ешение.- На рис. 15.39б, в, г изображено 3, принятых к рассмот-рению, тела. Для каждого из них можно составить систему из трёх линейно независимых уравнений равновесия. В каждую из этих систем войдёт по 4 неизвестных. На первый

взгляд может показаться, что встретилась статически неопределимая конструкция. Но это не так – дело в том, что в составленную совокупность уравнений (в количестве ) войдёт не двенадцать (), а всего 6 неизвестных.

Решение многовариантное. Приводим одно из них.

Для тела по рис. 15.39б: ; .

Для тела по рис. 15.39в: ;

; .

Для тела по рис. 15.39г: .

В приведенном решении рассматривалось 3 тела. Можно было ограничиться рассмотрением 2-х – по рис. 15.39б-в, или б-г, или в-г.

81

П

К условию примера 15.14

РИМЕР 15.14.-На конструкцию из сложно сочленённых частей; система сил плоская; в рассматриваемой теме задача средней тяжести

Дано: части соединены как указано на рис.15.40; известны все активные силы - и геомет-рические размеры - ; и т.д.

О

Рисунок 15.40

К решению примера 15.14

пределить реакции в сочленениях (ограничиться сос-тавлением схемы решения – без алгебраических подробностей и вычис-лительных операций записать одну, из многих возможных, последова-тельность рассмотрения уравнений равновесия, приводящую к определению реакций в сочленениях ).

Р

Рисунок 15.41

ешение.- Принятые к рассмотрению тела изображены на рис. 15.40а,б,в,г. При этом, горизонтальная и верти-кальная реакции угловой опоры К вначале приведены к равнодейству-ющей, которая, затем, представлена составляющими . Аналогично, в виде двух составляющих, представ-лены и реакции угловой опоры Е.

Для тела AD: ;

Для тела СК: ;

Для тела ВЕ: ;

Для тела СВ: ; ;

И, наконец, из для тела AD, из для тела СК и из для тела ВЕ, находятся силы .

82

1 15.345.8. Явления сопротивления скольжению и качению тел. Формы их учёта в инженерно-расчётной практике

С

К вопросу о сопротивлении скольжению тела

15.35

ущность явления сопротивления скольжению тел ясна из изображений, представленных на рис.15.42. На рис.15.42б: G – вес тела, - веса чаш для гирь; Q – суммарный вес набора размещённых в чаше гирь (рассматривается как переменная величина); весами нитей и сопротивлением в блоках пренебрежено (ввиду их малости).

Вобщем случаеG и Q не обязательно веса тела и набора гирь. В общем случае - перпендикулярная, а- параллельная опорной поверхности составляющие равнодействующей приложенных к телу активных сил (всех внешних сил, за исключением реакции опорной поверхности).

Будем называть: - прижимающая и- побуждающая проскальзывание силы. При наличии скольжения тела А по опорной поверхностиназывают движущей силой.

Рисунок 15.42

и - составляющие равнодействующей реакции опорной поверхности;- нормальная реакция;- сопротивление проскальзыванию.

В зависимости от кинематического состояния тела называют либо силой сцепления -(когда тело покоится), либо силой трения скольжения -(когда тело скользит по опорной поверхности).

Г

15.36

рафик по рис. 15.42в отображает результаты экспериментального изучения явления сопротивления скольжению (при этом, на графике модули сил иизображены в одном масштабе).- критическое значение силы, побуждающей проскальзывание тела (характеризуется тем, что бесконечно малое превышение этого значения приводит тело в движение).

При учёте явления сопротивления скольжению оперируют также понятиями «коэффициент сцепления» и «коэффициент трения скольжения».

83

Коэффициент сцепления () - это безраз-мерная величина, равная отношению модуля силы сцепления к модулю нормальной составляющей реакции опорной поверхности.

К

оэффициент трения скольжения () - это безразмерная величина, равная отношению модуля силы трения скольжения к модулю нормальной составляющей реакции опорной поверхности.

Изучением трения учёные занимаются с давних пор. В частности, в трудах Герона Александрийского (Греция; жил примерно в 1-2 веках н.э.) имеются рекомендации смазывать жирами и маслами колёса театральных механизмов; имеются рекомендации в каких случаях в трущихся соединениях применять железо, и в каких медь. Понятие о коэффициенте трения скольжения найдено в трудах Леонардо да Винчи (Италия; годы жизни – 1452-1519), который он рекомендовал принимать равным 0,25.

К началу 3-го тысячелетия накопилось много попыток создания теорий трения - адгезионная, молекулярная, молекулярно-кинетическая, адгезионно-деформационная, энергетическая и др. Выявлено, что коэффициент трения скольжения зависит от материалов соприкасающихся тел, от разделяющих их окисных плёнок, покрытий, смазочных материалов, от макрогеометрии соприкасающихся поверхностей (одно дело, когда тела соприкасаются по плоскостям и другое, когда по цилиндрическим желобам; этот вопрос подробнее рассматривается в курсе теории механизмов и машин), от микрогеометрии соприкасающихся поверхностей, от удельных давлений, скоростей скольжения, температуры и других факторов.

Н

39

о, несмотря на всё это, теория трения ещё далека от своего совершенства. И в то же время инженеры обязаны уметь решать конкретные технические задачи с учётом трения и не когда-нибудь, а сегодня. И они умеют это делать. Быть может не столь точно и изящно, с учётом многофакторности, как это будет делаться в четвёртом тысячелетии, но умеют (с достаточной для большинства случаев практики точностью).

Сегодня в инженерно-расчётной практике учёт трения скольжения базируется на следующих 2-х предпосылках:

вконкретно встречающихся случаях существуют относительно широкие интервалы значений нормальных реакций, когда коэффициенты трения скольжения могут считаться постоянными

(т.е. изменяющаяся в некотором интервале величина заменяется средним её значением);

84

к

15.37

оэффициент трения скольжения практически равен максимальному значению коэффициента сцепления.

П

15.40

ри этом, значения коэффициентов трения скольжения определяют из специальной и справочной литературы, либо проводят специальные опыты (см. с. 185-186) и затем опираются на полученные в них результаты. Но вопрос о выборе коэффициентов трения скольжения не является предметом теоретической механики и в дальнейшем будем считать их заданными.

Заметим лишь, что при использовании литературных данных и результатов специально проводившихся опытов по определению коэффициентов трения скольжения, необходимо соблюдать осторожность – можно учесть факторов (материалы соприкасающихся тел и их покрытия, тип смазки и пределы изменения удельного давления, макро- и микрогеометрию и т.д.), но упустить ()-й, например при трении полозьев о снег не учесть его плотность, или температуру воздуха, или скорость скольжения, и получить коэффициент трения скольжения на порядок и более отличающийся от действительного его значения.

При решении задач на равновесие тел с учётом сил сопротивления скольжению удобно использовать

15.38

условие сохранения покоя тела -

(из рис.15.42б видно, что 15.38 получается из условия равновесия ).

П

К вопросу об угле и

конусе трения

ри расчётах с учётом сопротивления скольжению используют также понятия «угол трения» и «конус трения».

Угол трения (на рис.15.43а - ) – это угол между полной реакцией () опорной поверхности и нормальной () её составляющей при наличии скольжения тела. Из введенных понятий следует, что

т

Рисунок 15.43

15.39

ангенс угла трения равен коэффициенту трения скольжения, т.е..

Если движущей силе придать всю совокупность возможных направлений, то отрезок (по рис. 15.43а) опишет конус. Чаще всего он оказывается круговым – см. рис.15.43б).

Из понятия «конус трения» и опорного факта 15.38 следует:

85

если равнодействующая от прижимающей () и побуждающей скольжение () сил находится внутри конуса трения (на рис.43б см. ), то покоящееся тело не может быть выведено из этого состояния, независимо от значения модуля этой равнодействующей;

прижимаемое к опорной поверхности тело из состояния покоя может быть выведено лишь в том случае, если равнодействующая от прижимающей и побуждающей скольжение сил расположена внешним образом к конусу трения (на рис.15.43б см. ).

Подробное рассмотрение явления самоторможения тел не является предметом теоретической механики. Заметим лишь, что его не следует абсолю-тизировать – надо подходить конкретно и здраво. Если активные силы строго постоянны, то теоретическое предсказание явления самоторможения высоко-доверительно. При наличии же вибраций ими нельзя пренебрегать. В частности, рекомендуем помнить, что составители нормативных документов, определяющих безопасную эксплуатацию ответственных машин, весьма осторожно относятся к явлению самоторможения. Так, для грузоподъёмных механизмов использование явления самоторможения допускается лишь при обязательном наличии в констру-

к

К вопросу о сопротивлении тел качению

ции ещё и тормоза. Нельзя игнорировать и тот факт, что идя вдоль проезжей части дороги вы то в одном, то в другом месте обнаруживаете валяющиеся гайки и болты, принадлежавшие когда-то проезжавшим здесь автомобилям и велосипедам - обнаруживаете детали соединений, которые обычно принято считать самотормозящимися.

В

Рисунок 15.44

технике широко распростра-нены сочленения с перекатывающи-мися друг по другу телами – колёса транспортных средств катятся по железным и автомобильным дорогам; по дорожкам подшипников качения катятся шарики и ролики (цилинд-рические, конические, бочкообразные, игольчатые; стальные и нестальные; сплошные, витые; и прочие).

86

Т

15.41

ела качения, несмотря на их конструктивные различия, могут быть объединены одним геометрическим образом - катком - цилиндром, расположенным на горизонтальной плоскости - см. рис.15.44, где О – центр катка, А – точка касания катка с опорной поверхностью (в предположении абсолютной твёрдости соприкасающихся тел).

Действующие на каток активные силы (без учёта реакции опорной поверхности) приведём к точке А. При этом, обозначим и назовём:

- прижимающая каток сила (часто – это часть веса машины);

- побуждающая проскальзывание сила;

- поворачивающий момент.

Опыт показывает (см. рис.15.44д): если поворачивающий момент не превосходит некоторого предельного значения, каток покоится. Объясняется это образованием микроволны (впереди катка – см. рис.15.44б), а также явлением прилипания (образованием, с последующим разрывом, мостиков сварки между отдельными микроплощадками позади катка – окисные плёнки на микропиках взаимодействующих поверхностей разрушаются в местах контакта и между появляющимися ювенильными поверхностями начинают действовать молекулярные силы).

П

15.42

о причине упругих деформаций взаимодействующие тела соприкасаются по поверхности, имеющей хотя и малую, но конечную площадь. Распределённую по контактной площадке реакцию на каток также приводим к точке А (на рис.44в см.,и). Назовём:

- момент сопротивления качению;

- нормальная несмещённая реакция на каток;

- сопротивление проскальзыванию (сила сцепления - когда проскальзывания нет; сила трения скольжения - когда тело проскальзывает по опорной поверхности).

С целью перехода к рассмотрению главной расчётной величины, характе-ризующей качение тел, момент сопротивления качению и нормальную несмещённую реакцию на катокприводим к одной силе, что представлено на рис.15.44г - равнодействующая оти пары с моментомобозначена. Она оказалась паралельна АО и смещена относительно О на

.

будем называть «нормальной смещённой реакцией на каток».

87

То значение момента , при котором тело начинает катиться, называют критическим значением момента сопротивления качению (на рис.15.44д -).

П

лечо нормальной смещённой реакции на каток, соответствующее критическому значению момента сопротивления качению, называют коэффициентом трения качения ().

В отличие от безразмерного коэффициента трения скольжения, коэффициент трения качения измеряется в единицах длины - обычно в сантиметрах. По этой причине можно называть«плечом сопротивления качению».

Значения коэффициентов трения качения определяют из справочной литературы, либо по результатам специально поставленных опытов.

Вопрос о выборе коэффициентов трения качения не является предметом теоретической механики и в дальнейшем считаем их заданными. Заметим лишь (как и для коэффициентов трения скольжения), что при выборе коэффициентов трения качения необходимо соблюдать осторожность; в частности, можно встретить рекомендацию – «коэффициент трения качения колеса по рельсу» (в других источниках – «мягкой стали по мягкой стали») равен 0,005см, но из других, более доверительных источников, узнать, что, например в случае качения ходовых колёс подъёмных кранов, эта величина находится в интервале 0,03-0,12см и зависит, кроме материалов взаимодействующих тел, от диаметра колёс и типа рельса.

Из изложенного без дополнительных рассуждений видно, что

условием отсутствия качения является соотношение

условие же качения -

П

К примеру 15.15

РИМЕР 15.15.- На трение качения

Дано:установили, что коэффициент трения качения труб по настилу с достаточным уровнем надёжности не будет превышать 0,15см; диаметры самокатящихся труб будут не менее 6 см.

Определитьминимальный угол наклона настила, обеспечивающего самотранспортировку труб.

Решение.- Изображаем силы, действующие на каток – см. рис. 15.45. Модуль поворачивающего момента:

Рисунок 15.45

.

Модуль нормальной реакции (из ):.

Из условия качения: . Откуда.

88

П

К условию примера 15.16

РИМЕР 15.16.- На сопоставление трения скольжения с трением качения

Д

Рисунок 15.46

ано: имеется две возможности перемещения тела весом по горизонтальной поверхности (см. рис. 15.46),- волоком по стальному листу (с коэффициентом трения скольжения ) и на трубках, диаметром см; коэффициенты трения качения трубок по телу и по опорной поверх-ности одинаковы - см.

Определить модули движущих сил по первому () и второму () вариантам перемещения заданного тела.

Р

Рис.47

К решению примера 15.16

ешение.- Для перемещения волоком:

кН.

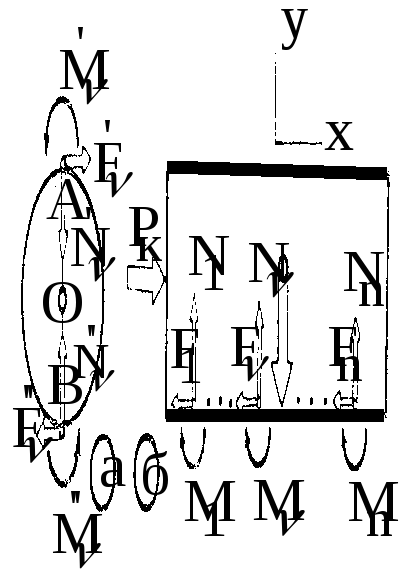
Теперь рассматриваем вариант качения. На рис.15.47а:

- моменты сопротивления, нормальные несмещённые реакции и силы сцеп-ления, действующие на -тую трубку в точках А и В соприкосновения с перемещаемым телом и полом.

Вначале установим связь между и. С этой целью для-той трубки:

; ;

из условия её качения: . И теперь, из,

.

Принимаем к рассмотрению перемещаемое тело (см. рис.15.47б). Изображаем действующие на него активные силы - и, а также реакции трубок (- их количество). Из; и, наконец, из,

кН, что в 40 раз меньше

силы, требующейся для перемещения этого тела волоком.

89