18. Простые движения твёрдого тела

18.1. Поступательное движение

-

18.1

это движение тела, при котором любой взятый в нём отрезок прямой перемещается параллельно своему начальному положению.

Примеры поступательного движения тел: лифт; вагон (или автомобиль) на прямолинейном участке дороги; движение люльки со скамейками на аттракционе «колесо обозрения» - см. рис.1; движение шатуна в механизме шарнирного параллелограмма - рис.18.2.

Колесо обозрения Механизм шарнирного параллелограмма

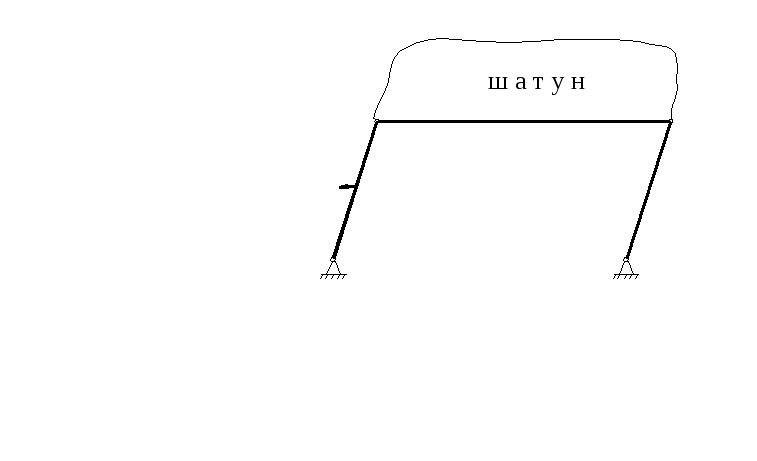
Рисунок 18.1 Рисунок 18.2

Замечания:

п

18.2

ри поступательном движении траекторией точки может быть любая линия, в том числе и пространственная;

т

Поршень в теле вращающегося диска

18.3

очки поступательно движуще-гося тела описывают одинако-вые траектории (при наложении совмещающиеся друг с другом);

п

18.4

оступательное движение - понятие относительное,

что иллюстрировано на рис.18.3, где:

1 – подпружиненный поршень; 2 - вращаю-щийся диск; 3 - корпус механизма; поршень относительно диска движется поступательно, относительно корпуса - нет.

З

Рисунок 18.3

акон(о скоростях и ускорениях поступательно движущихся тел):

в

18.5

се точки поступательно движущегося тела имеют одинаковые скорости и одинаковые ускорения.

107

П

К закону об одинаковости скоростей и ускорений

риводим рассуждения, позволяющие теоретическим путём получить закон5.–

Пусть (см. рис.18.4)- радиус-векторы произвольных точекпоступательно движущегося тела.

Т.к. , где

(в соответствии с понятиями абсолютно тврдого тела и поступательного его движения), то, после взятия от записанного равенства производной по времени, получаем:.

А

Рисунок 18.4

налогично:и т.д.

Т.к. , то,

после взятия производной по времени от последнего равенства, получаем и равенство ускорений точек Использование ранее изложенных методов для теоретического перехода к закону 18.5 завершено. Итак:

в

18.6

се точки поступательно движущегося тела имеют одинаковую кинематику. Иначе: кинематика поступательного движения сводится к кинематике точки.

18.2. Вращательное движение

-

18.7

это такое движение, когда у тела имеется подмножество частиц, неподвижных во времени относительно какой-либо оси системы отсчёта. Такую ось называютосью вращения.

В

К понятию вращательного движения

рамках рассматриваемого подраздела ось вращения будем обозначать буквой, а её орт -. Примеры вращательных движений: ротор электродвигателя, карусель, дверь и т.п.

При описании вращательного движения полуплоскость системы отсчёта, начинающуюся с оси вращения, называют неподвижной полуплоскостью (или полуплоскостью отсчёта - см. рис.5).

П

Рисунок 18.5

олуплоскость, начинающуюся с оси вращения и связанную с телом, называютподвижной полуплоскостью.

108

18.2.1. Об угловых скоростях и ускорениях

Процесс перемещения подвижной полуплоскости относительно неподвижной называют поворотом тела. Количественной его характеристикой является

у

18.8

гол поворота – это двухранный угол между подвижной и неподвижной полуплоскостями, рассматриваемый как алгебраическая величина - больше нуля тогда, когда мысленное движение в направлении изображающей его круговой стрелки оказывается встречным по отношению к движению конца стрелки часов при условии, что циферблат виден с положительного направления оси вращения.

в

18.9

ектор поворота – это вектор, определяемый из математического выражения: .

у

18.10

гловая скорость () – это кинематическая мера вращательного движения твёрдого тела, определяемая как первая производная по времени от вектора поворота, т.е.

, где

- проекция угловой скорости на ось вращения.

Единицей измерения угловой скорости является радиан за секунду, что в записях обозначают: , либо (редко) -.

В практике чаще частоту вращения оценивают числом оборотов в минуту (об/мин). Т.к. за одну минуту тело поворачивается нарадиан, а за секунду на угол в 60 раз меньший, то

у

18.11

гловая скорость тела (речь идёт о модуле), выраженная в радианах за секунду, с числом оборотов в минуту связана соотношением

У

18.12

гловое ускорение () – это кинематическая мера вращательного движения твёрдого тела, определяемая как первая производная по времени от угловой скорости, т.е.

, где

- проекция углового ускорения на ось вращения.

109

Единицей измерения углового ускорения является .

Подобно тому, как это делалось при рассмотрении кинематики точки,

принято различать:

если , т.е.- вращениеравномерное;

если - вращениепеременное

(при -ускоренное; при -замедленное);

если - вращениеравнопеременное

(при -равноускоренное; при -равнозамедленное).

18.2.2. О линейных скоростях (иначе: О скоростях

О связи между

и

точек вращательно движущегося тела)

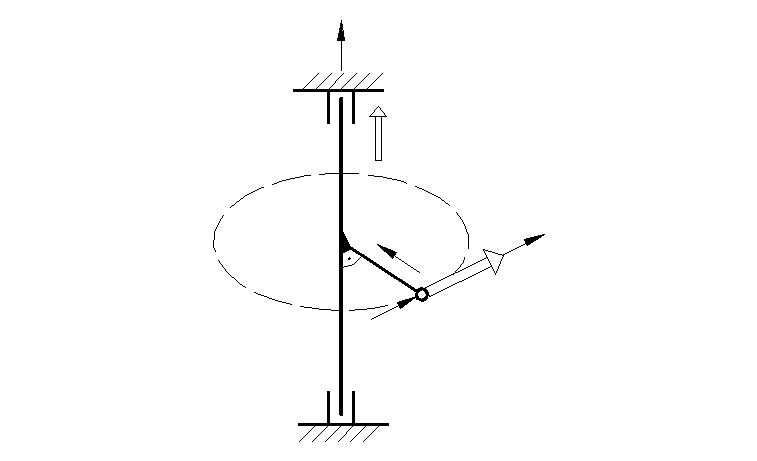
На рис.6 изображён стержень, вращающийся вокруг перпендикулярной ему оси.

Т.к. ,, то изполучается

ф

Рисунок 18.6

18.13

ормула для вычисления модуля скорости точки вращательно движущегося тела -.

Ц

О связи между

и

ентральное место в современном курсе теоретической механики занимает векторный метод. По этой причине выведем формулу, в которой скорости точек вращающегося тела выражаются через угловую его скорость. С этой целью изображаем рис.7, из которого видно, что ортысвязаны соотношением:.

Т.к. , то.

Учитывая 18.13, получаем:

Рисунок 18.7

.

Но , а.

Поэтому получаем:

110