30.3.4. Случай плоского движения

30.16

.

Итак:

суммарная мощность, развиваемая силами, приложенными к плоско движущемуся телу, определяется суммой двух мощностей:

п

30.15

ервая () вычисляется по формуле поступательного движения тела (в предположении, что точки приложения всех сил имеют одинаковые скорости, равные скорости центра тяжести тела);

вторая составляющая () вычисляется по формуле враща-тельного движения (во вращательном движении тела относительно центромассовой системы отсчёта).

30.4. О независимости работ и мощностей внутренних сил от выбора систем отсчёта

Внутренние силы встречаются лишь двойками (попарно) и являются противоположными. Одна из таких двоек внутренних сил изображена на рис.30.6,

273

где и - пара взаимодействующих частиц любой,

О независимости работ и мощностей внутренних сил от выбора систем отсчёта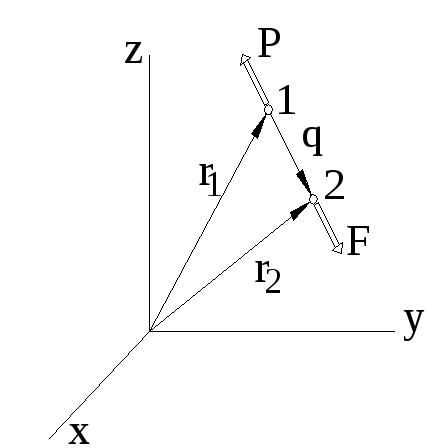

принятой к рассмотрению, механической системы; - сила, с которой точка действует на точку ; - сила, с которой точка действует на точку ; и - радиус-векторы точек в произвольной системе отсчёта ; - вектор, начинающийся в первой точке и заканчивающийся во второй, переменный (в системе ) как по модулю, так и по направлению.

И

Рисунок 30.6

меем ввиду, что в соответствии с законом о равенстве действия и противодействия

.

Суммарная элементарная работа рассматриваемой двойки внутренних сил:

18

.

То же выражение будет получено и при любой другой системе отсчёта (как угодно перемещающейся относительно ).

Очевиден аналогичный результат и для суммарной мощности рассматриваемой спарки внутренних сил. Итак:

У

19

твёрдого тела суммарные работы и мощности внутренних сил равны нулям.

1. В механических системах, состоящих из перемещающихся друг относительно друга тел, суммарные работы и мощности внутренних сил не равны нулям, но они не зависят от выбора систем отсчёта;

30.17

20

2. В рамках рассмотрения одной и той же механической системы при вычислении работ и мощностей одних внутренних сил можно брать различные системы отсчёта;

3. С целью упрощения вычислений суммарной работы двойки противоположных сил удобно брать систему отсчёта, в которой точка приложения одной из её составляющих оказывалась бы неподвижной.

Практически нет ни одной машины, в которой бы отсутствовали подвижные соединения (зубчатые, вращательные, поступательные пары; подшипники качения, скольжения; и т.д.). В них всегда присутствуют силы трения.

274

При вычислении работ и мощностей, идущих на преодоление сил трения в подвижных соединениях, удобно одно из сопряжённых тел принимать за неподвижное. Тогда эти величины будут определяться лишь через относительные скорости (для мощностей) и относительные перемещения (для работ).

В

а

о многих механических системах содержатся упругие элементы (цилиндрические пружины, пластинчатообразные рессоры и т.п.). Каким бы не было абсолютное движение этих элементов, вычислять мощности и работы внутренних их сил также можно по относительным скоростям и перемещениям.