3 К выводу формулы для вычисления работы силы тяжести0.2. Примеры вычисления работ сил для часто встречающихся случаев

30.2.1. Работа силы тяжести на

конечном перемещении точки её приложения

П

8

усть материальная точкаперемещается из положенияв положениепо произволь-ной траектории- см. рис.3.

.

Рисунок 30.3

9

.

Принято называть: - геодезическая высота начального положения точки;- геодезическая высота конечного положения точки;- разность геодезических высот. Таким образом:

- работа, совершаемая силой тяжести, не зависит от формы траектории точки её приложения и равна произведению модуля силы тяжести на разность геодезических высот начального и конечного положений этой точки.

30.2.2. Работа упругой силы на конечном перемещении точки её приложения

На рис.30.4: - тело, к которому приложена упругая сила ; - положение тела, соответствующее недеформированному состоянию пружины;

270

- координ

К выводу формулы для вычис-ления работы упругой силы

ата, определяющая некоторое текущее положение тела .

В

30.10

соответствии с законом Гука , где - жёсткость пружины, - величина её деформации. Изображённый на рис.30.4 треугольник называют эпюрой упругой силы.

Работу упругой силы при перемещении тела из некоторого деформированного состояния, определяемого координатой , в недеформи-рованное (), называют полной работой упругой силы.

Рисунок 30.4

30.11

Итак,

п

30.8

олная работа упругой силы (при переведении упругого элемента в недеформированное его состояние) определяется формулой

.

Неполная работа упругой силы (допустимо сокращение: «работа упругой силы») – это работа, совершаемая упругим элементом при переходе из одного своего деформированного состояния в другое. Ясно, что:

р

30.9

абота упругой силы равна площади той части треугольной своей эпюры, которая расположена между координатами, отличающими одно деформированное состояние упругого элемента от другого.

30.2.3. Работа гравитационной силы

Н

К выводу формулы для вычисления работы гравитационной силы

30.12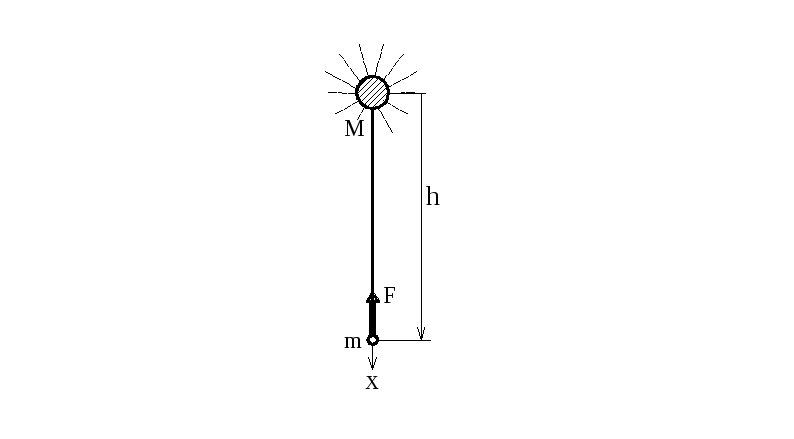

а рис.30.5: - притягивающий центр (Земля, Солнце и т.д.); - притягиваемая масса; - сила притяжения, определяется по закону Ньютона: . Ось начинается в , - некоторое конечное значение координаты .

П

30.13

олная работа гравитационной силы () – это работа, которую она совершит при перемещении притягиваемой массы из бесконечности в положение, определяемое расстоянием . Выведем формулу для её

Рисунок 30.5

271

вычисления:

.

Итак,

полная работа гравитационной силы (совершаемая ею при перемещении притягиваемой массы из бесконечности в положение, определяемое расстоянием от притягивающего центра) определяется формулой .

Самостоятельно получите результат:

работа гравитационной силы, затрачиваемая на перемещение притягиваемой массы из положения в определяется формулой

.

30.3. Формулы для вычислений суммарных мощностей сил, действующих на твёрдые тела

30.3.1. Случай поступательного движения

Мощности, развиваемые отдельными силами:

.

Т.к. тело движется поступательно, то

просто .

Поэтому суммарная мощность:

, т.е.:

с

15

уммарная мощность сил, приложенных к поступательно движущемуся телу, определяется как мощность отдельной силы, равной главному вектору действующих на это тело сил и точка приложения которой перемещается со скоростью тела.

8.3.2. Случай сферического движения

, т.е.:

суммарная мощность сил, приложенных к сферически движущемуся телу, определяется как мощность отдельной, приложенной к этому телу, пары сил, момент которой равен главному моменту действующих на тело внешних сил.

272

30.3.3. Случай вращательного движения

Вращательное движение – частный случай сферического.

Пусть осью вращения является . Тогда

, т.е.:

с

30.13

уммарная мощность сил, приложенных к вращательно движущемуся телу, определяется как произведение главного момента внешних сил относительно оси вращения на проекцию угловой скорости на ту же ось.

При решении конкретных задач часто приходится иметь дело с постоянными моментами сил и, при этом, определять их работу на конечных перемещениях. Применительно к такому случаю имеем:

(после интегрирования), т.е.:

с

30.14

уммарная работа сил на конечном повороте тела определяется как произведение главного момента внешних сил относительно оси вращения на произошедшее приращение угловой координаты.