14.9. О центрах тяжести

С пренебрежимо малой погрешностью для подавляющего большинства решаемых задач можно считать, что сила тяжести – это равнодействующая параллельно-распределённой системы сил, приложенных к частицам тела со стороны поля земного тяготения.

Вес тела – это модуль силы тяжести.

Удельный вес – это вес единицы объёма тела.

Центр тяжести тела – это такая его точка, через которую проходит сила тяжести, независимо от положения тела, относительно Земли.

Понятие о центре тяжести тела ввёл Архимед (287-212 до н.э.) – в трактате «О весах» он писал: «Центр тяжести тела – это точка пересечения отвесных линий при подвесе этого тела за различные точки».

Для определения положений центров тяжести тел используют экспериментальные и теоретические способы.

Из экспериментальных наиболее распространены способы подвешивания и взвешивания тел.

С

14.14

пособ подвешивания: тело два раза подвешивают на нити (цепи, тросе, верёвке и т.п.) и находят точку пересечения двух экспериментально установленных направлений. С точки зрения получения минимальной погрешности, угол между определяемыми направлениями надо принимать близким к 90^о.

С

14.15

пособ взвешивания целесообразно использовать для тел протяжённой формы. Рекомендуем студентам «открыть» (разработать и описать) его самостоятельно (после изучения раздела «Равновесие тел»).

Экспериментальные способы удобно использовать в случае тел сложной конфигурации и составленных из деталей, имеющих разные удельные веса материалов, из которых они изготовлены.

Однако, несмотря на простоту, экспериментальные способы не всегда применимы. Например, при отсутствии конструкции (что имеет место на стадии проектирования устройств и сооружений), при больших размерах тел, при отсутствии возможности прикрепить к телу гибкую связь.

53

П

Способ разбиения тела на части

ри теоретическом определении положений центров тяжести тел сложной конфигурации используют приём разбиения исходного тела на части -

его представляют разделённым наменьших тел (см. рис.6), весаи положения () центров тяжести которых известны; тогда, в соответствии с законом Вариньона:

, где

Рисунок 14.3

- вес исходного тела.

Из 14.13 видно, что положения центров тяжести однородных тел зависят от геометрических форм, но не от разновидностей материалов. В связи с этим, оперируют также понятиями: «центр тяжести объёма», «центр тяжести плоской фигуры», «центр тяжести линии». Чтобы отличать одно от другого в формулах 14.13 вместо можно условиться писать другие буквы: в первом случае -, во втором -, в третьем -. Этот результат легко видится, если веса начать выражать через удельный вес (), или через вес единицы площади плоской фигуры, или через вес единицы длины линии. Например,и ясно, что, как величина, не зависящая от номера частицы тела, из уравнения уйдёт – окажется и в числителе, и в знаменателе.

Из 14.13 рекомендуем самостоятельно получить и такой результат:

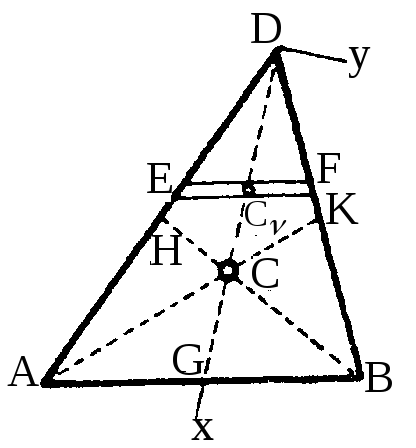
ц

О центре тяжести треугольника

ентр тяжести однородного тела располо-жен в плоскости симметрии, на оси симметрии, в точке симметрии (если таковые имеются).

Переходим к рассмотрению основных приёмов, применяемых при определении центров тяжести однородных тел простых конфигураций.

Центр тяжести однородного треугольника находится на пересечении его медиан.

Сформулированный результат можно получить следующими рассуждениями.-

Р

Рисунок 14.4

азбиваем треугольник на бесконечно большое число бесконечно узких полосок, параллельных основанию АВ. ЕF – одна из них, -тая (см. рис. 14.4).

54

М

14.17

едиана ДG пересекает -тую полоску посередине (в точке). В соответствии с 14.14 ордината её центра тяжести () равна нулю. Таким образом, распределённая по поверхности треугольника система сил тяжести сводится к тяжёлой линии - к медиане ДG.

Т

14.18

.к. для любой из расматриваемых элементарных полосок, то на основании 14.13 заключаем: центр тяжести треугольника расположен на медиане ДG.

Аналогично приходим к выводу о том, что центр тяжести треугольника расположен и на медиане АК.

Н

14.19

о тело имеет лишь один центр тяжести. Следовательно, он расположен на пересеченииDG и AK.

О

О центре тяжести дуги окружности

14.20

сталось лишь напомнить (из элементарной геометрии): точка пересечения медиан делит каждую из них на два отрезка, один из которых (примыкающий к вершине треугольника) в два раза больше второго.

Ц

14.16

ентр тяжести однородной дуги окружности (см. рис.14.5) расположен на её оси симметрии и отстоит от центра этой окружности на расстоянии

где - радиус окружности;

- половина центрального угла, на который дуга опирается.

Р

Рисунок 14.5

езультат 14.16 можно получить следующим образом.-

Ось (см. рис.14.5) направляем так, чтобы она оказалась осью симметрии рассматриваемой дуги. Тогда (в соответствии с 14.14), .

Длина дуги: .

Представим её состоящей из бесконечно большого числа бесконечно малых дуг, одна из которых (длиной ) изображена на рисунке. Тогда:

.

Ниже приведенные результаты 14.17-14.20 получите самостоятельно:

55

ц

О центре тяжести кругового сектора

ентр тяжести однородного кругового сектора отстоит от центра круга на расстоянии

, где

- радиус круга; - половина секторного угла;

у

Рисунок 14.6

однородной полусферы (рис.14.7) центр тяжести отстоит от её основания (от экваториальной окружности) на расстоянии, равном половине радиуса;

уоднородного полушара (см. рис.14.8) центр тяжести отстоит от основания-круга на растоянии трёх восьмых радиуса.

центр тяжести однородной пирамиды (и конуса) расположен на отрезке, соединяющем центр тяжести основания с вершиной и отсто-ит от вершины на расстоянии, равном трём четвертям этого отрезка.

О центре тяжести полусферы

О центре тяжести полушара

Рисунок 14.7

Рисунок 14.8

Куб. На нём пирамида

ПРИМЕР 14.1.- Вычислить координаты центра тяжести тела по рис.14.9.

м – длина ребра куба. .

Решение.- - Центр тяжести расположен на оси симметрии (на ) -м.

Рисунок 14.9

м.

56