26. Закон о движении центра масс в произвольных системах отсчёта

26.1. Математическое выражение закона

Ускорение центра масс механической системы относительно инерциальных и произвольных троек осей обозначаем, соответственно, и.

Приняв инерциальную систему отсчёта за неподвижную, а произвольную за подвижную, в соответствии с теоремой сложения скоростей записываем:

,

а

где

- переносное и- кориолисово ускорения центра масс.

Подставляем (а) в математическое выражение закона-аксиомы о движении центра масс. Получаем математическое выражение

закона о движении центра масс в произвольных системах отсчёта:

26.1

, где

и- называют эйлеровыми (переносной и кориолисовой) силами инерции.

Переносная сила инерции () - это математическое понятие; это вектор, противоположно направленный вектору, определяемому произведением массы системы на переносное ускорение её центра, который имеет размерность силы и в процессе математических операций может рассматриваться как обычная сила.

Предоставляем возможность студенту определение кориолисовой силе инерции дать самостоятельно.

К принципу относитель-ности Галилея

26.2. Принцип относительности Галилея

и Геоцентрическая система отсчёта

Пусть - инерциальная система отсчёта (см. рис.1). Тогда в ней, как уже рассмотрено в разделе 25, справедливо математическое соотношение

.

Пусть, далее, система отсчёта

с

Рисунок 26.1

находящимся в ней наблюдателем, поступательно, прямолинейно и равномерно движется относительно, причём с ка-

199

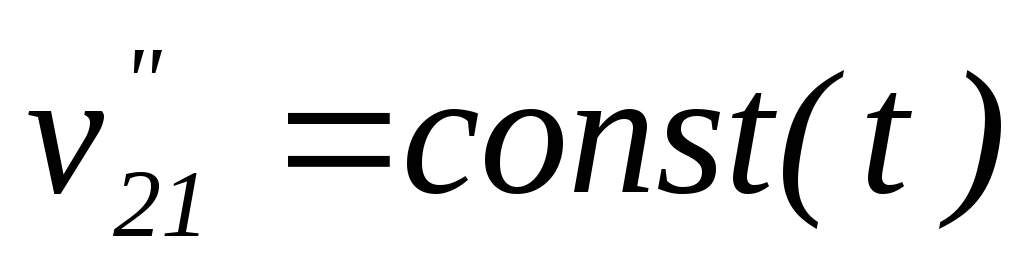кой угодно скоростью , т.е. со скоростью, либо, либо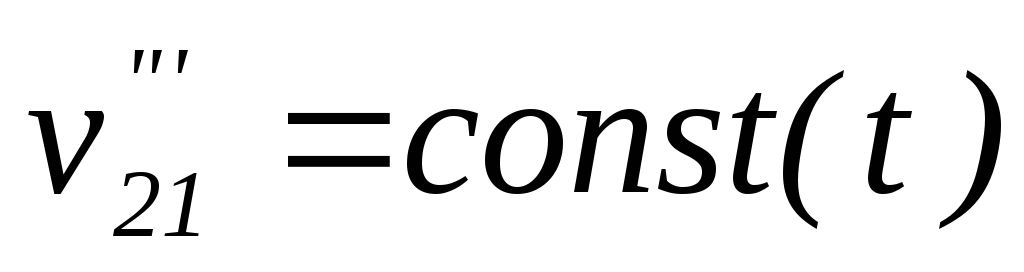и т.д.

Т.к. вторая система перемещается относительно инерциальной поступательно, прямолинейно и равномерно, то . Поэтому:

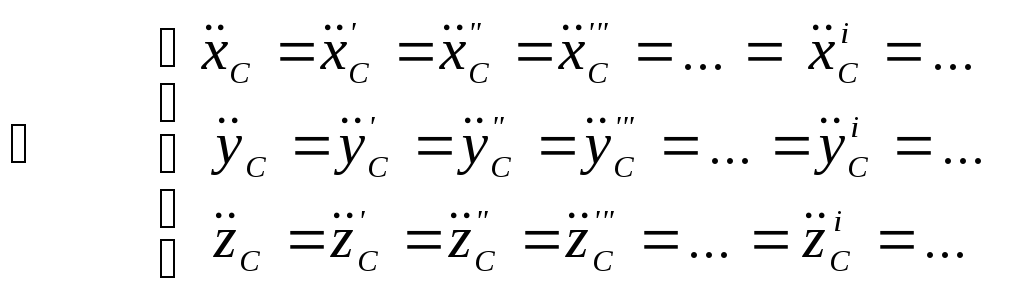
т.е. получаем, что имеется множество систем отсчёта, в которых движение центра масс механической системы, находящейся под действием той или иной любой системы сил, описывается одинаковыми дифференциальными уравнениями и все эти системы отсчёта перемещаются друг относительно друга поступательно, прямолинейно и равномерно.

Если, к тому же, во всех системах отсчёта одинаковы и начальные условия -

,

то центр мас будет описывать в них одинаковые траектории.

Вот как это явление просто и доходчиво описывал Галилей (в «Послании к Инголи», а в 1632 году повторил в «Диалоге»):

«В большой каюте под палубой какого-либо крупного корабля закройтесь с другими наблюдателями. Устройте так, чтобы в ней были мухи, бабочки и другие летающие насекомые, аквариум с плавающими в нём рыбками. Возьмите также сосуд с узким горлышком и прилаженным над ним другим сосудом, из которого вода бы капала, попадая в узкое горлышко нижнего сосуда.

И пока корабль стоит неподвижно, наблюдайте внимательно, как эти насекомые будут с одинаковой скоростью летать по каюте в любом направлении, вы увидите, как рыбки будут двигаться безразлично в направлении какой угодно части аквариума. Все капли воды падая будут попадать в стоящий внизу сосуд с узким горлышком. И вы сами, бросая какой-либо предмет вашему другу, не должны будете бросать его с большим усилием в одну сторону, чем в другую, если только расстояние одинаково. А когда вы начнёте прыгать двумя ногами с места, то на одинаковые расстояния сместитесь по всем направлениям.

200