П

К условию примеров 25.4 и 5

з

роанализироватьеё движение.

Р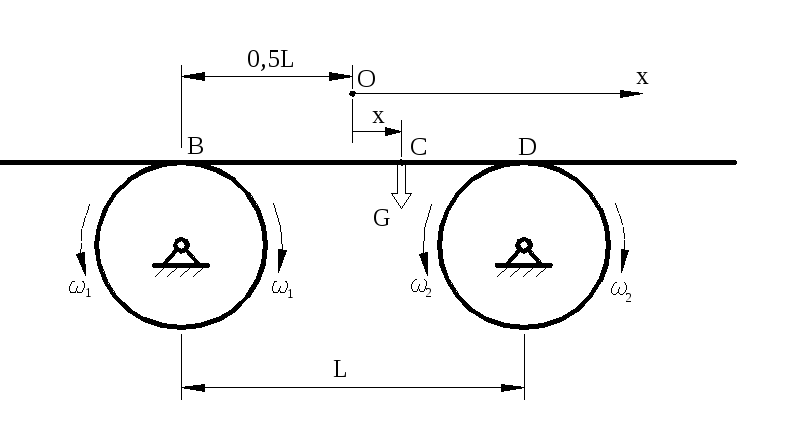ешение.- Силы трения скольжения в точках В и D, как известно из статики, определяются по формулам:

а

(применительно к рассматриваемому случаю на рис. 5 они изображены сплошными стрелками).

П

Рисунок 25.4

К решению примеров 25.4 и 5

ренебрегая толщиной доски, из уравнений

и

п

25.12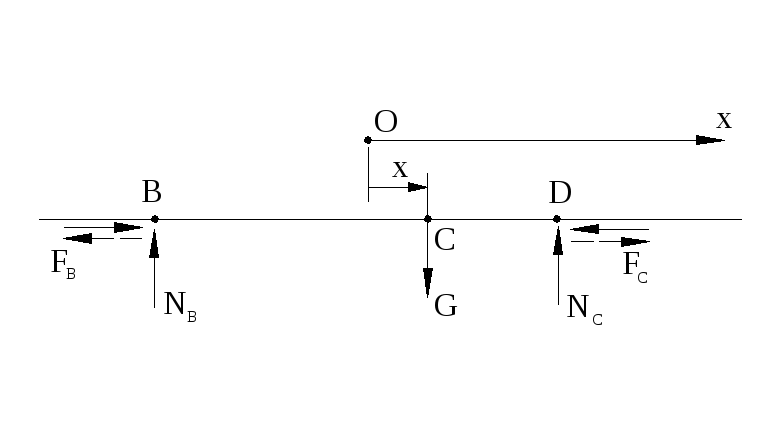

олучаем (допустимость использова-ния записанных уравнений будет ясна после изучения принципа Даламбера):

б

;

в

Рисунок 25.5

Векторное уравнение, отображающее закон движения центра доски:

г

.

Проектируя его на ось , получаем:

д

.

Из (а), (б), (в) и (д):

е

, где

это уже встречавшаяся (см. 25.9) каноническая форма дифференциального уравнения свободных колебаний. Его решение:

ж

, где

постоянные определяем из начальных условий. Для этого учитываем, что

185

.

Откуда: и т.д.

Теперь используем (ж): .

Итак, получаем: , т.е. .

Замечание: из (е) видно, что механическую систему по рис. 4 можно использовать в качестве установки для определения коэффициента трения скольжения экспериментально-теоретическим способом – т.к. круговая частота с периодом колебаний связана соотношением , то получается

формула для экспериментально-теоретического способа определе-ния коэффициентов трения скольжения

, где

м/с² – ускорение свободного падения, - конструктивный параметр; - экспериментально определяемый период колебания.

ПРИМЕР 25.5.- Доска на противоположно вращающихся барабанах. Силами трения растягивается - это пример на определение движения центра масс при силах, являющихся функцией координаты; характер движения неустойчивый. Вспомогательная значимость примера – показ на конкретном примере, что «подобия» и «похожести» по одним параметрам сопоставляемых систем (явлений, процессов и т.п.) далеко не всегда являются основаниями к утверждениям типа «да это тоже самое».

Дано. - Механическая система, рассматривавшаяся в примере 25.4 (изображена на рис.25.4 и 5) – та же конструкция (м; вес доски - и прочие одинаковости); тот же коэффициент трения (), те же начальные условия (при м); причём, барабаны вращаются как и в примере 25.4 в противоположных направлениях, но произведен реверс электродвигателей - направления вращения для примера 25.5 указаны прерывистыми линиями.

Требуетсяпроанализировать движение доски - возможность схода её с барабанов. И, если анализ предскажет такое событие, то вычислить момент времени , в который центр тяжести С доски будет проходить через точкуD(или В) её соприкосновения с барабаном.

186

Решение.- Ясно, что решение примера 25.5 повторяет решение примера 25.4 до (г). Различия начинаются с (д) - получается

,

т.е. получается дифференциальное уравнение

е

, где .

Находим 1-й интеграл дифференциального уравнения (е).

Т.к.

,

то (е) принимает вид:

ж

.

И в левой, и правой частях видны табличные интегралы. Берём их -

з

Т.к. , то из (з): .

Вновь видим табличные интегралы. Интегрируем:

.

Из полученного уравнения движения видно монотонное возрастание с увеличением времени . Вывод: доска через определённый промежуток времени сойдёт с барабанов.

Вычисляем время , по истечении которого координата центра доски окажется равной половине (после чего она под действием собственного веса безвозвратно потеряет горизонтальное положение и свалится с барабанов):

187

.

Откуда с.

ПРИМЕР 25.6.- Вывод формулы для вычисления максимально возможной скорости катера. Это пример на определение движения центра масс в случае, когда главный вектор внешних сил является функцией квадрата модуля скорости

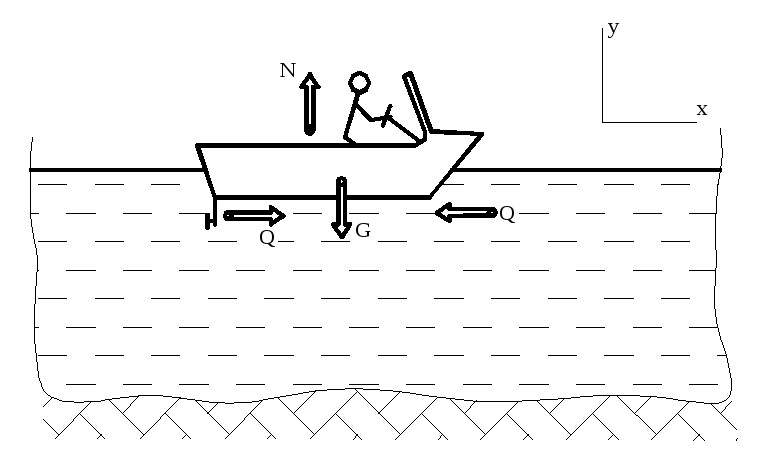
Дано. - Движущая катер сила (приложена к винту со стороны воды - рис.25.6) - .

К условию и решению

примера 25.6

- вес катера с людьми и прочим находящимся в нём грузом (, где - масса, - ускорение свобод-ного падения тел). - выталкива-ющая сила. - сопротив-ление движению (со стороны воды); ; - модуль скорости катера. При .

О

Рисунок 25.6

пределитьзависимость модуля скорости катера от времени –

Установить также максимально возможное значение этой скорости.

Решение.- Основное уравнение динамики материальной точки применительно к рассматриваемому случаю

.

Проектируем составленное векторное равенство на ось и получаем:

, где

.

В левой и правой частях получившегося дифференциального уравнения содержатся табличные интегралы. Интегрируя получаем:

188

Используя начальные условия находим постоянную и получаем:

Откуда, после алгебраических преобразований:

.

Из последнего выражения видно, что модуль скорости имеет максимальное значение при , т.е.

.

Решения примеров 25.3-6 требовало составления одного дифференциального уравнения второго порядка. Переходим к иллюстрации более сложных случаев - когда материальная точка имеет две степени свободы и приходится составлять систему двух дифференциальных уравнений 2-го порядка.

Ограничиваемся рассмотрением трёх близких друг к другу по инженерно-физической сущности случаев пассивного (без наличия движущей силы) полёта тела: пример 25.7 – без учёта сопротивления воздуха и два примера (25.8 и 25.9) - с учётом сопротивления.

189

ПРИМЕР 25.7.- Прыжок воднолыжника - это пример на определение движения центра масс в случае, когда главный вектор внешних сил является постоянной во времени величиной, движение криволинейное (в исторически значимых примерах, изложенных в поразделе 3.4, рассматривался более простой случай – прямолинейное движение).

Дано: начальная скорость (; м/с, ); высота (м) расположения в начале полётной фазы центра масс механической системы «спортсмен-лыжи» над горизонтальной плоскостью, в которой этот центр масс окажется в момент касания лыж с водной поверхностью (см. рис.25.7).

Определить дальность () и максимальную высоту полёта () воднолыжника.

К условию и решению примера 25.7

Рисунок 25.7

Решение.- Записываем основное уравнение динамики материальной точки (центра масс системы «спортсмен-лыжи») применительно к рассматриваемому случаю

а

.

Проектируя (а) на осьполучаем:

б

Откуда: .

Взяв второй интеграл от (б), получаем:

в

(постоянная интегрирования равнялась нулю по той причине, что время принято отсчитывать от момента, когда центр масс воднолыжника находится на оси ).

Теперь проектируем векторное равенство (а) на ось. Получаем:

190

г

.

При . Поэтомуи:

д

.

Теперь интегрируем дифуравнение (д). Получаем:

.

Т.к. при тои, поэтому:

е

.

Момент времени, соответствующий обозначаем. В этот момент времени(потому, что вектор скорости на вершине траектории горизонтален).

Из математического анализа известно: чтобы установить максимум функции (а речь идёт о траектории) необходимо взять от неё производную и приравнять нулю. Такая производная уже имеется - см. (д),откуда и получаем:

ж

Теперь (ж) подставляем в (е) и получаем:

з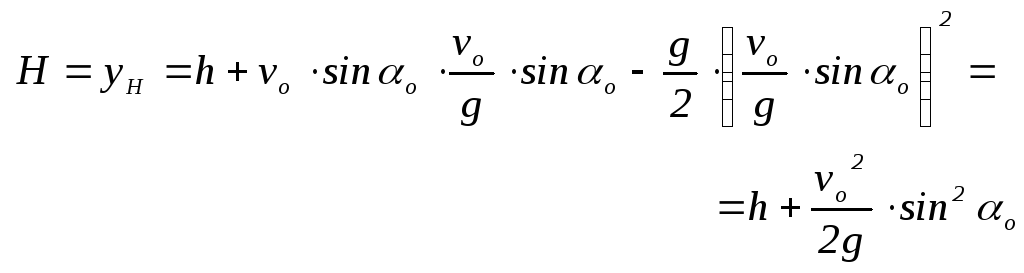

или, после числовой подстановки, м.

Момент касания лыжами водной поверхности () устанавливаем из(е) -

т.к. при то получаем: .

Откуда (решая квадратное уравнение):

и

.

Теперь, после подстановки (и) в(в), получаем:

191

к

.

И, наконец, из (и) и(к) после численных подстановок находим:

м.

ПРИМЕР 25.8*.- Полёт тела (снаряда), брошенного под углом к горизонту с учётом сопротивления воздуха - это пример на определение движения центра масс в случае, когда главный вектор внешних сил является функцией вектора скорости

Дано. - Начальная скорость бросания (- модуль, - угол её расположения относительно горизонта – см. рис. 25.8). Сила сопротивления , где - вес тела, - скорость его центра тяжести, - постоянная во времени величина (коэффициент).

Т

К условию и решению примера 25.8

р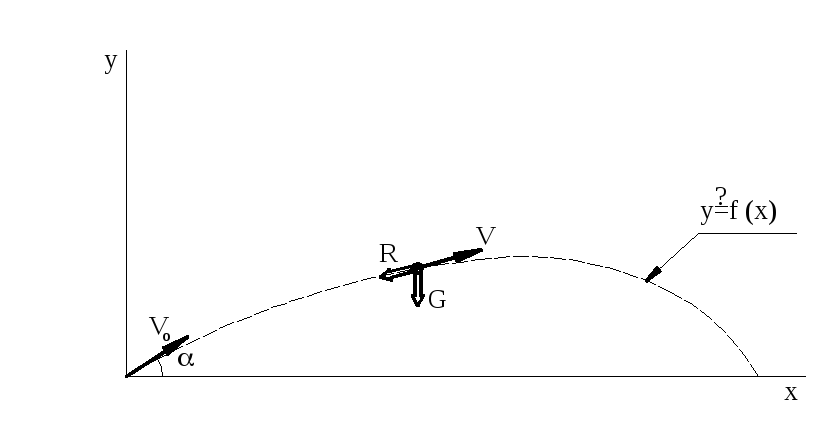ебуется Аналитически описать уравнение траектории центра тяжести тела – в форме .

Решение.- Основное уравнение динамики материальной точки применительно к рассматриваемому случаю:

.

Проектируем записанное вектор-ное уравнение на оси и :

а

б

И

Рисунок 25.8

з (а): .

В левой и правой частях последнего выражения видим табличные интегралы. Интегрируя и используя начальные условия, получаем -

192

.

Интегрируем последнее выражение и используем начальные условия:

.

Откуда

и, поэтому:

в

.

Из (в):

г

.

Из (г), после алгебраических преобразований:

д

.

Теперь интегрируем дифуравнение (б):

.

После подстановки :

.

После переноса в правую часть, вновь видим табличные интегралы. После интегрирования получаем:

.

193

Используяначальные условия находим:

.

Поэтому

.

Подставляя в последнее выражение (г) и (д), окончательно получаем:

.

Замечание: опыты, проводившиеся со стрельбой артиллерийских снарядов, показали, что имеются диапазоны скоростей, когда сопротивление среды оказывается пропорциональным скорости (в баллистике - это закон Сиаччи); этот случай и был рассмотрен в примере 25.8. Но чаще сила сопротивления атмосферы направлена по касательной к траектории и пропорциональна квадрату модуля скорости летящего снаряда. Об этом в следующем примере.

ПРИМЕР 25.9.- Об исследовании движения снаряда, когда сила сопротивления среды определяется формулой - это пример, иллюстрирую-щий необходимость часто прибегать к численным методам решения.

В рассматриваемом случае дифференциальные уравнения движения принимают вид:

.

«Чистое» аналитическое решение записанной системы дифуравнений авторам неизвестно. Подобные уравнения рекомендуем решать численно - методом последовательных шаганий.-

.

От бесконечно малых переходим к малым конечным величинам

.

Длину временного шага принимаем, к примеру, 0,0001 с.

1

16

-й шаг.

Учитывая известные (), определяем значения , соответствующие моменту времени :

194

.

.

2-й шаг (определяются значения для конца 0,0002-й секунды)

.

.

3-й шаг (определяются значения для конца 0,0003-й секунды)

.

.

И так далее

25.7. Обобщённая оценка проблемы решения задач динамики. Рекомендуемые подходы

В рассмотренных в предыдущем подразделе примерах силы были постоянными, функцией вектора скорости, квадрата скорости, времени и координаты, материальная точка имела 1 и 2 степени свободы. Даже в этих, относительно простых случаях, были видны сложности, с которыми инженеру приходится сталкиваться при попытках получить точные аналитические решения составленных дифференциальных уравнений.

В общем же случае главный вектор внешних, действующих на систему сил может являться одновременной функцией и времени, и координаты, и скорости; движения могут описываться не только отдельными дифференциальными уравнениями, но и системами. В связи с этим, рекомендациями ответим на естественный, возникающий у будущих специалистов, вопрос: «Какой в текущий момент жизни человеческого общества видится схема подхода инженера к возникающим в практической его деятельности задачам динамики, решаемым через интегрирования»?

1. П

   25.13

   режде всего, необходимо владеть опорными фактами теоретической механики, допустимыми методами их преобразования и, на этой основе,уметь составлять применительно к конкретным механическим системам соответствующие уравнения.

195

2. С точки зрения точностей, обозримости получаемых результатов и дальнейших их анализов, наиболее привлекательны «чистые» аналитические решения. И такие случаи довольно часты. По этой причине в проигрывающем положении оказывается тот инженер, который в составленных дифференциальных уравнениях не заметит табличных интегралов и начнёт использовать другие подходы к решению.

3. Если попытки самостоятельно проинтегрировать составленные дифференциальные уравнения не увенчались успехом, не забывать, что предшествующие поколения накопили большой опыт аналитических решений дифференциальных уравнений (часто увековечивая этим своё имя – Матье, Риккати, Абель, Бернулли, Клеро, Ламе, Лаплас, Лежандр и т.д.) и настоящий инженер обязан этим пользоваться. В частности, необходимо знать, что имеются, к примеру, такие книги: «Камке Э. Справочник по обыкновенным дифференциальным уравнениям.- М.: Наука, 1976.- 576 с.»; «Двайт Г.Б. Таблицы интегралов.- М.: Наука, 1966.- 228 с.» и другие подобные.

4. Если не привела к успеху и рекомендация по п.3, целесообразно проконсультироваться с математиками–специалистами по дифуравнениям.

5. Если и п.4 не помог, не отчаивайтесь – переходите к численным методам решения (что, в частности, было иллюстрировано примером 25.9). При этом, следует иметь ввиду, что при использовании современных ЭЦВМ подавляющее большинство возникающих в широкой инженерной практике задач динамики на интегрирование поддаются численным методам решения, что обязывает нас закончить советы возвратом к первой рекомендации, как к главной для будущего инженера, желающего стать хорошим специалистом; как к рекомендации, обепечивающей инженеру приоритет и инициативу перед другими специалистами, подключаемыми к процессу решения конкретных задач механики.