П

К примеру 30.2

РИМЕР 30.2.- Определение коэффициента трения скольжения по пройденному пути

Д

Рисунок 30.8

ано. – Тело в положении «1»имеет скорость (см. рис.30.8). На него действуют сила тяжести , нормальная реакция и сила трения скольжения . Пройденный телом до остановки (на рис.8 положение «2») путь равен .

Требуется.- Определить коэффициент трения скольжения .

Решение.- Кинетическая энергия тела: в первом его положении - ; во втором - .

.

Т

К забивке сваи

аким образом, получаем: .

ПРИМЕР 30.3.- Забивка сваи

Дано. – Груз (рис.30.9), весом Н, падает с высоты м. Он, ударяя по свае , внедряет её в грунт на глубину см.

Т

31.1

ребуется.- Определить среднюю силу сопро-тивления грунта () внедрению в него сваи.

Решение.- Кинетическая энергия системы «груз-свая»: в начале удара - ;

в конце удара - .

Работа средней силы сопротивления грунта:

Рисунок 30.9

.

Итак,

.

Что вы можете сказать относительно и заметили ли, что при решении задачи закон об изменении кинетической энергии применён 2 раза?

281

31. Метод кинетостатики

31.1. Введение в раздел

Применение рассматриваемого опорного факта теоретической механики даёт возможность решать методами статики многие задачи динамики. Особенно удобно использовать этот метод для учёта динамических нагрузок при силовых расчётах инженерных сооружений и конструкций.

Формирование метода связано с именами Я.Бернулли (1654-1705), Я.Германа (1678-1733), Л.Эйлера (1707-1783) и других отечественных учёных. Иногда, поэтому, его называют петербургским принципом. Но наиболее весом вклад в развитие и внедрение в жизнь этого метода у Жана Даламбера (1717-1783). По этой причине для рассматриваемого опорного факта широко распространено иное название - принцип Даламбера.

31.2. Понятия, условия и уравнения динамического равновесия

Располагаясь в инерциальной системе отсчёта принимаем к рассмотрению произвольную механическую систему. Представляем её состоящей из частиц. - масса, скорость, ускорение и радиус-вектор -той из них; и - равнодействующие внешних и внутренних приложенных сил. Развиваемые равнодействующими и мощности: .

Записываем основное уравнение динамики для -той частицы:

а

.

Вектор

называют силой инерции -той частицы.

З

д

амечание.- Термин «сила инерции» уже встречался – в разделе 4. Но там речь шла о переносной () и кориолисовой () силах инерции, которые принято называть эйлеровыми силами инерции. Даламберова сила инерции () - это другое понятие; это понятие, связанное с ускорением частицы относительно инерциальной системы отсчёта. Если даламберову силу инерции связать с ускорениями относительно неинерциальной системы, то она окажется суммой трёх составляющих – двух эйлеровых и относительной () сил инерции, т.е.:.

Рекомендация 1.- Среди учёных иногда возникают споры о физическом смысле сил инерции. Эти полемики требуют глубокого знания науки о понятиях, философии и физики, что обучающимися ещё не накоплено. Во избежание мало-

282

продуктивных затрат учебного времени советуем воздерживаться от вхождения в подобные дискуссии. Рекомендуем до окончания ВУЗа ограничиться лишь таким пониманием:

с

30.2

31.4

31.5

ила инерции – это математическое понятие; это вектор, имеющий размерность силы, по модулю равный произведению массы на ускорение, направленный противоположно ему, который можно включать в систему действующих на частицу сил и в процессе математических преобразований обращаться с ним, как с обычной силой.

С учётом введенного понятия (а) принимает вид:

б

.

(б) мысленно представляется как столбец записанных друг под другом равенств – второе под первым, третье под вторым и т.д. (с индексами).

Почленно складывая эти равенства (внешние силы с внешними, внутренние с внутренними, силы инерции с силами инерции), получаем:

в

.

Возвращаемся к (б). Каждую строку умножаем векторно слева на соответствующие радиус-векторы , а затем расположенные по столбцам однотипные члены складываем между собою:

г

.

Почленно складывая столбец (г), получаем:

31.6

.

Из статики известно, что главные вектор и момент внутренних сил равны нулю. Получили

условия динамического равновесия -

30.3

31.7

-

главные вектор и момент от внешних и даламберовых сил инерции равны нулю для любой механической системы.

283

Проектируя условия динамического равновесия на оси координат, получаем

уравнения динамического равновесия -

-

Для учёта сил инерции можно использовать формулы:

.

(они прямо следуют из законов о движении центра масс и об изменении кинетического момента).

31.3. Связь между главными моментами сил инерции относительно начал инерциальной и центромассовой систем отсчёта -

В предыдущем подразделе введено понятие главного момента сил инерции относительно центра инерциальной системы отсчёта. Преобразуем его. –

.

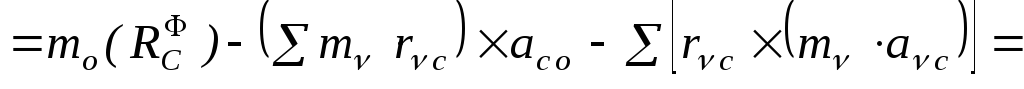
Итак:

-

г

8

лавный момент сил инерции относительно центра инерциальной системы отсчёта можно вычислять как сумму, составленную из главного момента сил инерции относительно начала центромассовой системы отсчёта и момента относительно центра от силы, приложенной к центру масс и равной главному вектору сил инерции.

Рекомендация 2.-

При рассмотрении конкретных механических систем силы инерции удобно группировать по отдельным телам.

284

31.4. Простейшие случаи учёта сил инерции

Поступательное Вращательное Плоское движение

движение тела движение фигуры

Рисунок 31.1 Рисунок 31.2 Рисунок 31.3

Для поступательно движущегося тела и ясно, что является равнодействующей сил инерции.

К рис.31.3: для любой частицы тела и, поэтому (из 29.6; с учётом того, что применительно к рассматриваемому случаю - это точка )

Приведение сил инерции стержня,

наклонённого к осивращения

и поэтому , т.е. силы инерции при приведении их к точке С дают силу и пару с моментом .

Ясно, что при вращательном движении вокруг точки (рис.2) , а - силы инерции приводятся к одной паре

Из приведенных примеров видно:

и

31.8

зученные в статике приёмы эквивалентных преобразова-ний обычных сил можно применять и к силам инерции.

Например, силы инерции стержня, наклонно расположенного к оси вращения, приводятся к равнодействующей по закону треугольной эпюры – см.рис.31.4.

Рисунок 31.4

285