П

Стержень за концы подвешен на двух нитях

РИМЕР 29.6.- Стержень подвешен за два конца. Одна нить перерезается

Дано. – Однородный стержень за концы А и В подвешен к потолку на двух нитях (см. рис.29.15). Одна из них (правая) перерезается.

Т

Рисунок 29.15

ребуется.- Найти натяжение левой нити на бесконечно малом промежутке времени, следующим сразу же за моментом перерезания правой нити.

Решение.- Принимаем к рассмотрению стержень. Внешними, действующими на

него силами, являются натяжение левой нити и сила тяжести стержня.

Из получаем: .

Из .

Из геометрии: . При малых : .

В

29.16

связи с этим, второе из составленных дифференциальных уравнений принимает вид: . Подставляем полученное в первое уравнение:

29.17

. Учитываем, что и получаем: .

П

Падение диска с разматыванием нити

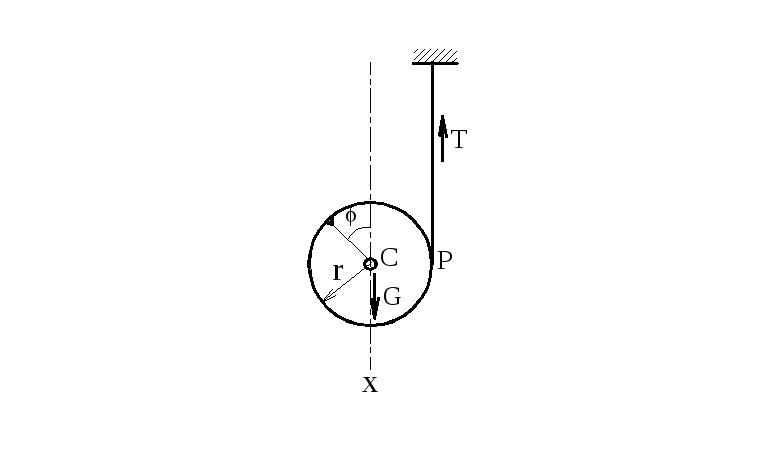РИМЕР 29.7.- Падение диска с разматыванием навёрнутой на него нити, свободный конец которой прикреплён к потолку

Дано. – На рис.29.16 изображён сплошной однородный диск с намотанной на него нитью, свободный конец которой прикреплён к потолку. - вес диска, - радиус; - натяжение нити.

Требуется.- Определить натяжение нити.

Р

29.18

ешение.- Принимаем к рассмотрению диск с прилегающим к его жолобу небольшим вертикальным участком нити (см. рисунок).

Т

Рисунок 29.16

раекторией центра тяжести диска является вертикальная прямая - это видно из .

259

- мгновенный центр скоростей для диска .

Из : . Подставляем это в последнее выражение предыдущей строки и получаем: .

Из : .

Объединяем уравнения двух последних строк, учитываем, что и находим: .

29.13. Начальные сведения о динамике произвольно и сферически движущихся тел

29.13.1. Уравнения, исторические сведения

Для математического описания произвольно движущегося тела относительно инерциальной системы отсчёта по аналогии с предыдущим подразделом можно ввести центромассовую систему отсчёта. Тогда:

-

уравнения, описывающие движение центра тяжести тела относительно инерциальной системы отсчёта ;

-

уравнения, описывающие сферическое движение тела в центромассовой системе отсчёта.

Но ... в отличие от динамики плоского движения, здесь имеются серьёзные трудности – проблемы возникают при разворачивании ().

Далее будем иметь ввиду сферического движение. Для него можно получить уравнения (см. следующий пункт – 29.13.2):

.

260

Их называют приведенными к форме Коши «динамическими уравнениями Эйлера» (или «уравнениями Эйлера-Пуассона», или «уравнениями Даламбера-Эйлера»). В них связаны с телом, причём являются главными его осями инерции.

У читателя должен возникнуть естественный вопрос: «Но где в уравнениях 29.18 координаты, которыми определяется положение тела относительно базовой системы отсчёта (инерциальной, или центромассовой»)?

Полная система дифференциальных уравнений сферического движения твёрдого тела получится тогда, когда к тройке уравнений 29.18 добавить ещё и

кинематические уравнения Эйлера в форме Коши:

29.19

(см., например, «Лунц Я.Л. Введение в теорию гироскопов.- М.: Наука, 1972.- 296с.»). При этом, напоминаем: - углы Эйлера (- собственного вращения, - прецессии, - нутации).

Естественно желание систему дифференциальных уравнений 29.18-19 решить чисто аналитически, да ещё для общего случая.

Этого до сих пор не удалось сделать. Аналитические решения известны лишь для частных случаев: Леонард Эйлер (в 1759 г. - ); Жозеф Луи Лагранж (1815 г. - ): Софья Ковалевская (1888 г. - , а центр тяжести расположен в экваториальной плоскости эллипсоида инерции) и некоторые другие.

Насколько важны и трудны были аналитические решения свидетельствует исторический факт с С.Ковалевской (1850-1891).- Французская академия наук трижды объявляла конкурс на лучшую работу по динамике сферического движения. Лишь на третий раз поступила стоящая работа (без фамилий – под девизами). Настолько стоящая работа, что жюри решило премию с 3000 франков увеличить до 5000.

В настоящее время уравнения 29.18-19 и компьютерная техника позволяют любой конкретно-числовой случай сферического движения решать и анализировать численным методом. Принципиальный подход к этому был дан в подразделе 3.6.

261