29.11. Закон об изменении кинетического момента в центромассовой системе отсчёта

Центромассовая система отсчёта – это система отсчёта, поступательно перемещающаяся относительно инерциальной системы и начало которой во времени совпадает с центром масс механической системы.

В

29.14

центромассовой системе отсчёта закон об изменении кинетического момента имеет ту же математическую форму, что и в инерциальной системе - , где

- центр масс любой, конкретно рассматриваемой механической системы;

15

- главный момент внешних сил относительно центра (который в общем случае перемещается относительно инерциальной системы с переменным ускорением);

- кинетический момент, определяемый по скоростям частиц относительно центромассовой системы отсчёта;

Результат 29.14 теоретически предсказывается теми же, многократно применявшимися, методами векторной алгебры. Вот этот преобразовательный процесс.-

.

В получившемся выражении первая сумма равна нулю - векторно перемножаются сонаправленные векторы. Во второй сумме добавляются, в отличие от преобразовательного процесса рассмотренного в подразделе 7.4, переносная и кориолисова силы инерции (т.к. центромассовая система не является инерциальной) -

.

Но т.к. центромассовая система – это система перемещающаяся поступательноотносительно инерциальной, то кориолисовы силы инерции для всех точек системы равны нулю. Равным нулю оказывается и главный момент от переносных сил инерции. И действительно:

.

Результат 29.14 распространить на произвольные системы отсчёта

нельзя. Объясните - почему?

256

29.12. Дифференциальные уравнения плоского движения твёрдого тела и примеры их применения

Н

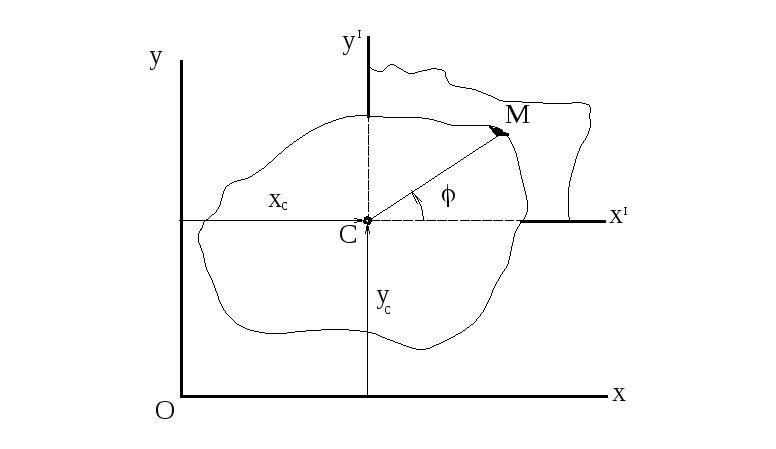
К динамике плоского движения

а рис.29.13 изображена плоская фигура, - центр её тяжести, - масса, - метка для отсчёта угловой координаты ; - инерциальная, - центромассовая системы отсчёта.

Объединяя опорные факты подразделов 25.1 и 29.7, получаем:

29.15

,

,

Рисунок 29.13

.

- дифференциальные уравнения плоско движущегося тела.

П

К качению кольца по наклонной плоскости

РИМЕР 29.5.- Качение кольца по наклоной плоскости

Дано. – Кольцо массой и радиусом скатывается по наклонной плоскости, характеризуемой углом (см. рис.29.14). Коэффициент трения скольжения кольца по наклонной плоскости - .

Требуется.- Область возможных значений угла (от 0 до 90^о) разбить на две – область чистого качения и область качения с проскальзыванием.

Р

Рисунок 29.14

ешение.- Принимаем к рассмотрению кольцо. Внешними для него силами являются: сила тяжести , нормальная

и касательная составляющие реакции плоскости (- сила сцепления – при отсутствии проскальзывания, либо - при наличии проскальзывания).

Рассматриваем случай отсутствия проскальзывания. Тогда точка соприкосновения кольца с плоскостью является мгновенным центром скоростей и, как известно из кинематики, имеет место равенство:

а

.

257

Теперь (а) дополняем тремя дифференциальными уравнениями 29.15 и, после совместного их решения, отвечаем на поставленный в задаче вопрос.-

ба

ва

г

.

Из (а) и (г):

д

.

Из (в) и (д):

еа

.

Условие отсутствия проскальзывания (из статики) имеет вид: , т.е. учитывая (е) получаем: . Откуда

условие отсутствия проскальзывания кольца по наклонной плоскости принимает вид: . Для кольца: . Поэтому в данной задаче условие отсутствия проскальзывания принимает вид:

.

Задание для самостоятельной работы: измените в условиях решённой задачи лишь одно – катится не кольцо, а сплошной однородный диск. До какого значения угла будет отсутствовать проскальзывание диска по наклонной плоскости?

258