29.10*. Основные экспериментально-теоретические способы определения моментов инерции тел

Не всегда моменты инерции тел можно установить чисто аналитическим путём. Две основные этому причины: геометрическая сложность форм и неоднородность материала.

К определению момента инерции автомобиля

29.10.1. Нахождение момента инерции тела через превращение его в физический маятник

с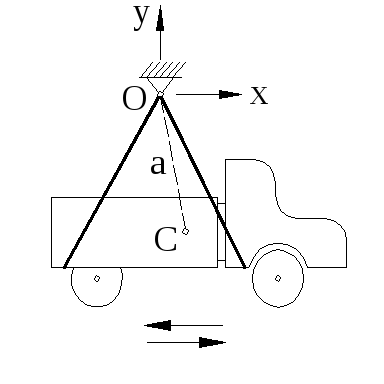экспериментальным определением

периода колебаний

Расчёты на устойчивость движения автомобилей по дорогам требуют знания их моментов инерции. Один из возможных путей такого определения представлен на рис.10:

Рисунок 29.10

.

З

К определению момента инерции шатуна

a

C

аписанные формулы являются прямыми следствиями результата 29.10. К моментам инерции относительно центральных осей автомобиля можно перейти с помощью математической связи между моментами инерции относительно параллельных осей, что рассмотрено в подразделе 28.5. Вопросы же определения положений центров тяжести рассматривались в статике.

П

Рисунок 29.11

ервая из записанных двух формул может быть использована и для определения момента инерции шатуна (см. рис.29.11) – деталь двигателя внутреннего сгорания (имеются практически в любом автомобиле, тракторе, тягаче и мотоцикле).

29.10.2. Нахождение моментов инерции тел cпособом маятника сравнения

Тело, момент инерции которого необходимо определить, превращают (см. рис.10 и 11) в физический маятник. Через ось подвеса перебрасывают нить с грузиком (например гайкой) на конце – это математический маятник в реальном исполнении. Длина математического маятника экспериментально подбирается такой, чтобы его колебания оказались синхронными колебаниям физического маятника. Тогда момент инерции тела относительно точки подвеса можно определять по формуле 29.12 - .

254

2 К определению моментов инерции тел способом крутильных колебаний9.10.3. Нахождение моментов инерции телcпособом крутильных колебаний

С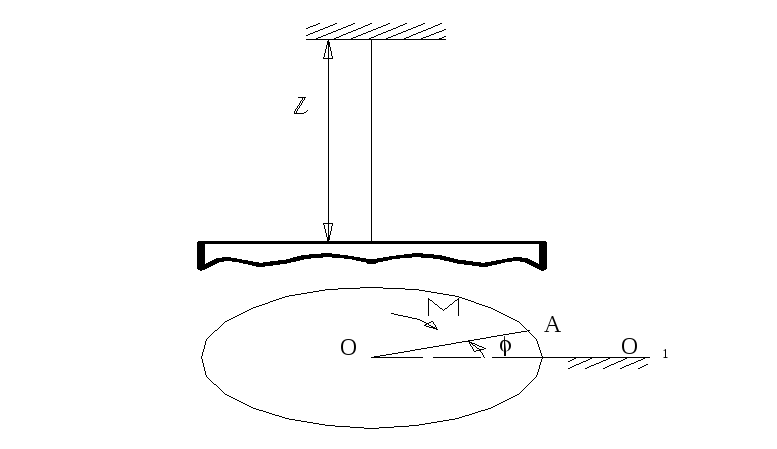хема устройства для нахождения моментов инерции тел способом крутильных колебаний изображена на рис.29.12: главный вид и под ним - вид сверху; - длина стальной проволоки, верхний её конец неподвижен, ось проходит через центр тяжести диска, нижний конец жёстко соединён с центром диска. - радиальная метка на диске; - неподвижная горизонталь, с которой совпадает метка в положении статического равновесия системы «проволока-диск»; - текущий угол закрученности проволоки;- момент, приложенный к диску со стороны проволоки.

При небольших углах закручивания (15-30^о, что практически всегда достижимо и зависит от длины )

,

где .

К

Рисунок 29.12

рутильная жёсткостьпроволоки определяется экспериментально, либо подсчитывается по известной из курса сопротивления материалов формуле.

На основании 29.7 записываем дифференциальное уравнение вращательного движения диска:

, где - экспериментально определяемый период колебаний системы «проволока-диск».

Практически более приемлема конструкция, в которой к нижнему концу проволоки жёстко прикреплён патрон от токарного станка, а уже в него закрепляется деталь с искомым моментом инерции.

Задание: вывести формулу, по которой можно определять момент инерции детали, закрепляемой в патрон от токарного станка.

255