33. Закон сохранения полной механической энергии

33.1. Введение в раздел

Имеются рядовые задачи, которые удобно решать с использованием рассматриваемого закона.

И

33.4

спользуется он и в общетеоретических построениях - уравнения Лагранжа 2-го рода для консервативных систем, теория устойчивости, малые колебания (см. подраздел 34.4 и раздел 35).

Кроме того, ещё и сегодня встречаются изобретатели вечных двигателей. Инженер обязан уметь объяснить окружающим бесперспективность работ над ними и направить энергию заблудившегося в своих научно-технических изысканиях человека на полезные обществу дела. Закон о сохранении полной механической энергии прямо и научно отвечает на этот вопрос.

Р

33.5

анее рассмотренные опорные факты динамики (закон о движении центра масс; законы об изменениях количества движения, кинетического момента и кинетической энергии; методы кинетостатики и возможных перемещений) справедливы для любых механических систем. О законе сохранения механической энергии этого сказать нельзя. Он применим лишь к консервативным системам.

33.1

Консервативная система – это механическая система, на которую действуют только потенциальные силы.

33.2. Понятие о потенциальных силах и потенциальной энергии. Критерии потенциальности

В подразделе 30.1 давалось понятие о работе силы на конечном перемещении точки её приложения -

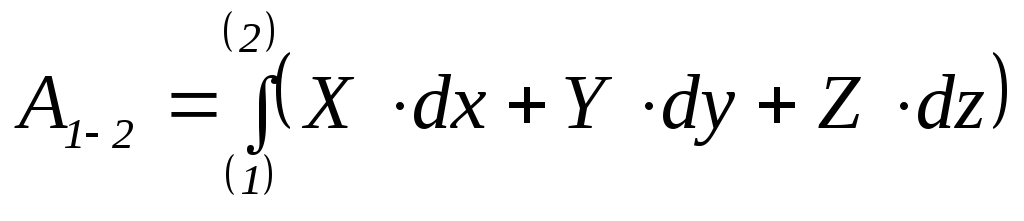, где

- проекции силы на оси координат.

33.2

Силу называют потенциальной, если производимая ею работа не зависит от формы траектории точки приложения, а зависит лишь от начального и конечного её положений.

Из определения следует две эквивалентные формы критерия потенциальности сил (одна удобна в одних случаях, вторая – в других).

Из курса высшей математики известно, что независимость криволинейного интеграла от формы пути равносильна равенству нулю этого интеграла вдоль всякой замкнутой кривой. Поэтому

п

33.3

ервая форма критерия для потенциальных сил:

если для силы соблюдено математическое условие , то она является потенциальной.

305

Из курса высшей математики известно и другое: чтобы криволинейный интеграл не зависел от формы пути, необходимо и достаточно, чтобы подинтегральное выражение, т.е. , было полным дифференциалом некоторой функции координат, т.е.

если сила потенциальная, то обязательно существует такая функция координат , которая удовлетворяет условию:

;

её называют силовой, а , где - произвольная постоянная, называют потенциальной энергией объекта (точки, тела) приложения потенциальной силы.

Из 33.4 следует

вторая форма критерия для потенциальных сил:

-

Покажем справедливость результата 33.5.

В соответствии с понятием полного дифференциала:

а

.

Из 33.4:

б

.

Из (а) и (б):

в

.

Взяв частную производную от по , затем от по и, учитывая известную из курса высшей математики теорему о независимости результата от последовательности взятия производных, получаем:

.

Второе и третье равенства критерия потенциальности 5 показываются аналогично.

306