28.6. Формула для вычисления момента инерции относительно произвольно ориентированной оси
Н
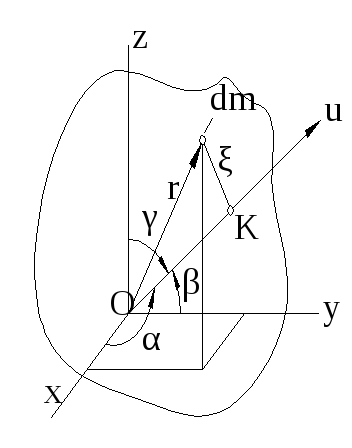
Рисунок 28.8К выводу формулы для момента инерции относительно произ-вольно ориентированной оси произ треугольника
а
рис.28.8.-
- произвольно связанная с телом М
прямоугольная система координат; осевые
и центробежные моменты инерции этого
тела относительно осей (
;
)
известны.
- проходящая через точку
произвольно ориентированная ось (её
орт
),
направляющие для неё углы (
)
известны.
- произвольная частица тела,
- её радиус-вектор,
- кратчайшее расстояние до оси
.
Сформулированную в заглавии раздела задачу решил ещё Эйлер – через углы, носящие его имя. Через направляющие косинусы, как рассматривается здесь, задачу впервые решил Коши (1827 г.). Вот эта зависимость:
.
С целью облегчения запоминания формулы,
обращаем внимание на то, что она состоит
из двух пар скобок; в первых скобках
содержатся все произведения осевых
моментов инерции на квадраты косинусов
«своих» углов (
).
Во вторых скобках содержится также
сумма всех произведений центробежных
моментов на косинусы своих углов (если
,
то косинусы углов
и
).
Докажем* справедливость формулы 28.9
а
.
Проектируем (а)
на ось
.
Получаем:
236