28.5. Формула, связывающая моменты инерции тел относительно параллельных осей

Н

К выводу формулы, связыва-ющей моменты инерции отно-сительно параллельных осей

Рисунок 28.5

а рис.28.5: С – центр тяжести тела массой;- центральная ось с известным моментом инерции.- ось, параллельнаяи проходящая от неё на расстоянии. Вывести формулу для вычисления момента инерцииотносительно оси.- масса элементарной частицы рассматриваемого тела (точка М).- начинающаяся в центре тяжести С ось, расположенная перпендикулярнои пересекающая (в точке А) ось. Из М опускаем перпендикуляры на

(точкаD) и(точка В). ОбозначаемMD,MB.

В соответствии с дававшимся понятием . По теореме косинусов:. Но- равно координате точки М по оси. Таким образом:

- записано на основании понятия центра тяжести, где- координата центра тяжести тела по оси. Ноначинается в точке С и, поэтому,. Таким образом:

233

момент инерции тела относительно произвольной оси больше момента инерции этого же тела относительно параллельной ей центральной оси - на величину, равную произведению массы тела на квадрат расстояния между рассматриваемыми осями, т.е.

.

К моменту инерции стержня относительно перпендикулярной, прохо-дящей через конец, оси

ПРИМЕР 28.1.- Формула для вычисления момента инерции стержня относительно перпендикулярной, проходящей через конец, оси

Д

Рисунок 28.6

ано. – Масса стержня , его длина (см. рис.28.6). Момент инерции стержня относительно перпендикулярной ему оси, проходящей через центр тяжести (относительно оси ), определяется формулой:.

Требуется.- Вывести формулу для определения момента инерции стержня относительно перпендикулярной ему, проходящей через конец, оси.

Решение.- Используя формулу 28.8, получаем:

.

П

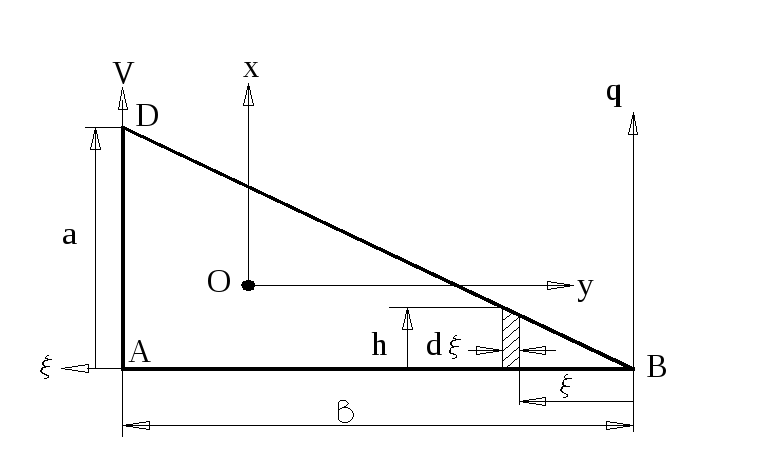
К моментам инерции треугольника

РИМЕР 28.2.-Вывод формул для вычисления моментов инерции треугольника относительно различных осей

Дано. – У однородного прямоугольного треугольника масса , а длины катетов и (как известно длина гипотенузы ). - центр тяжести.

Т

Рисунок 28.7

ребуется.- Вывести формулы для определения моментов инерции треугольника относительно изображённых на рис.7 осей, где - ось, дополняющая

и до правой прямоугольной системы координат.

Решение.- Вначале, воспользовавшись общей формулой 28.1, вычисляем момент

234

инерции треугольника относительно оси . Для этого треугольник разбиваем на элементарные полоски, параллельные осям . Одна из них изображена на рисунке: длина -, толщина - , расстояние от оси - . Тогда:

, где

- толщина треугольника, - площадь и - объём элемента; - плотность материала, из которого выполнен треугольник. Учтём в преобразованиях, что (из подобия треугольников) . Таким образом:

, где

в круглых скобках – площадь треугольника; в квадратных скобках – его объём; в фигурных скобках – масса треугольника. Итак:

.

В

28.9

оспользовавшись двоекратно формулой, связывающей моменты инерции относительно параллельных осей, находим и :

; .

В выражение для входит катет, перпендикулярный оси .Очевидно, поэтому, что .

.

Поясните: почему ?

235