28.4. Примеры на использование общих формул для определения моментов инерции тел

Стержень- это прямолинейно-протяжённое однородное твёрдое тело постоянного поперечного сечения. Как математическая модель стержень – это отрезок прямой, у которого одинаковые элементы длины имеют одинаковые веса.

28.4

Ось, проходящую через центр тяжести тела, называют центральной.

Считая известными массу () и длину () вывести формулу для вычисления момента инерции стержня относительно перпендикулярной ему центральной оси.

П

К выводу формулы для вычисления момента инерции стержня

редставляем стержень в виде бесконечно большого числа бесконечно тонких дисков, нанизанных на ось. Один из них, толщиной, изображаем (см. рис.3).

Если руководствоваться обозначениями, использованными на рис.3, то необходимо определить .

О

Рисунок 28.3

сновное значение имеют удалённые от оси частицы, но для них. Поэтому общая формула1в рассматриваемом случае принимает вид:

.

Т.к. , где- площадь поперечного сечения стержня;- объём выделенного элемента, а- плотность материала, то:

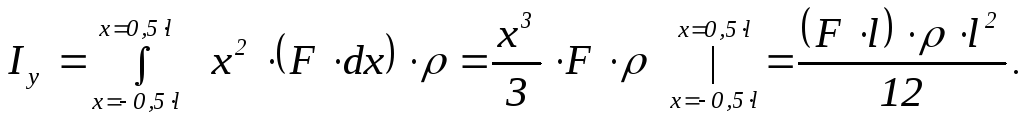
230

- это объём стержня;- его масса. Поэтому:

28.5

28.6б

- формула для вычисления момента инерции однородного прямолинейного стержня относительно центральной, перпендикулярной ему оси.

Цилиндр(однородный полый – как общий случай; сплошной однородный– как частный случай от общего, но в подавляющем большинстве встречающийся в расчётной практике;диск- сплошной однородный цилиндр малой длины).

Зная массу, внутреннийи наружныйрадиусы однородного полого цилиндра, определить его момент инерции относительно продольной оси симметрии. Если руководствоваться изображениями на рис.4, то определить момент инерции относительно оси-

П

К выводу формулы для вычисления момента инерции цилиндра

Рисунок 28.4

28.7

редставляем цилиндр состоящим из бесконечно большого числа бесконечно тонких (толщиной), вставленных друг в друга полых цилиндров.- радиус произвольного из них. Тогда, начиная с 28.1, получаем:

.

Выражение, заключённое в квадратных скобках, - это площадь поперечного сечения полого цилиндра. Она умножается на длину цилиндра; поэтому в фигурных скобках записана формула для вычисления объёма полого цилиндра. Т.к. объём полого цилиндра умножается ещё и на плотностьматериала, то окончательно получаем:

28.6а

- формула для вычисления момента инерции однородного полого цилиндра относительно его продольной оси симметрии.

231

Для диска и сплошного цилиндра и, поэтому:

- формула для вычисления момента инерции однородного диска (и сплошного цилиндра) относительно централь-ной оси, расположенной перпендикулярно торцам.

Задание студентам.- Если разделить 28.6ана 28.6б,то получится

.

Можно ли из этого сделать вывод, что при одинаковых длинах и наружных радиусах сплошного и полого цилиндров момент инерции относительно продольной оси будет большим у полого цилиндра? Подискутируйте с коллегами и установите истину.

Шар, конус. Двух рассмотренных примеров достаточно было для уяснения применявшегося «прямого метода» получения формул для вычисления осевых моментов инерции тел. Поэтому сообщаем лишь результаты:

момент инерции однородного шара относительно центральной его оси - ; момент инерции однородного конуса относительно его оси симметрии - .

Замечание: с целью облегчения запоминания обращаем внимание, что выражения для и отличаются лишь коэффициентами, которые соотносятся как числа Пифагора - .

Диск, центральная ось параллельна торцам

Обозначения осей сохраняем прежними (см. рис.4): центральная ось, перпендикулярная торцам диска;и- центральные взаимно перпендикулярные оси, расположенные в средней плоскости между торцами диска.

В соответствии с общими формулами 28.1

.

Применительно к диску в записанных интегралах (суммах) подавляющее значение имеют удалённые частицы, а для них ,, т.е. в рассматриваемых интегралах доляинженерно ничтожна и поэтому

232

28.8

.

Учитывая очевидное равенство и результат 28.6б получаем:

.