К силе действия струи брандспойта
ПРИМЕР 27.6.- Сила действия струи брандспойта
Д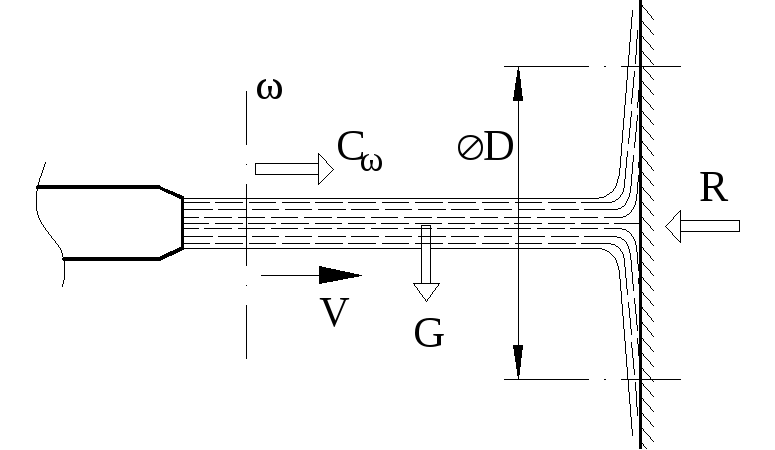
ано.
– Из брандспойта (см. рис.27.5) вытекает
струя воды со скоростью
м/с.
Диаметр наконечника
мм.
К стене струя расположена перпендикулярно
и о неё разбивается.
Требуется.- Определить давление струи на стенку.
Р
Рисунок 27.5
220
(диаметром
мм)
и цилиндрической поверхностью диаметра
(безразлично какого диаметра, но такого,
чтобы скорости частиц воды, пересекали
эту цилиндрическу поверхность
перпендикулярно).
Определим
внешнюю силу
,
действующую на принятую к рассмотрению
часть струи со стороны поверхности
стенки.
Записываем условие равновесия 27.11 применительно к рассматриваемому случаю:
=0,
где
-
сила тяжести принятой к рассмотрению
части струи - направлена вниз;
-
секундное количество движения втекающей
через сечение
жидкости (направлено внутрь рассматриваемого
объёма);
-
секундное количество движения вытекающей
элементарной струйки (с номером
),
она по нормали пересекает цилиндрическую
поверхность диаметра
;
-
это символ суммы секундных количеств
движения всех элементарных струек,
расположенных веером в плоскости стены.
Проектируем
составленное векторное уравнение на
направление
.
Получаем:
.
Через
входное круглое сечение (диаметром
м)
за 1 секунду протечёт столбец воды
длиной
.
Масса этого столбца:
,
где
кг/м3
- плотность воды.
Тогда секундное количество
движения
Итак,
давление, производимое на стену
рассматриваемой струёй воды равно
и направлено слева-направо.
Замечание:
если бы скорость струи была не
м/с
(как в рассмотренном приме-ре), а положим
м/с, то давление равнялось бы
! В эксперимен-тах достигаются скорости
струй до
м/с и более. Большой разрушительной
силе струй нашли применение в технике
- гидроотбойка угля (существуют так
называемые гидрошахты); струями воды
режут бумагу, дерево, стекло и пр.
221
27.7. Начальные сведения о ракетодинамике
27.7.1. Введение в подраздел
Вторая половина 20-века ознаменовалась широким вхождением в человеческую практику ракетной техники - и для военных целей, и для исследований космоса. Инженерные достижения в этой области огромны. Пока они, в большинстве своём, относятся к закрытой тематике. Но есть в этих вопросах и много хорошо известного, причём основополагающего. Инженер обязан это знать, ибо путь решения возникающих в практической его деятельности задач может пройти именно через знание основополагающих методов ракетодинамики.
Кроме того, инженер обязан обладать высокой технической культурой, умеющим на основе точного знания отвечать на многие интересующие людей вопросы. Один из них: «Нога человека уже ступила на Луну. Но может ли землянин побывать на планетах Солнечной системы (и непосредственно увидеть что там происходит)? Сможет ли побывать на планетах за пределами Солнечной системы»?
Ответить на такие волнующие Человечество вопросы позволяют уравнение Мещерского и вытекающие из него формулы Циолковского.