в частности, с книги «Батуев С.Г. и др. Инженерные методы исследования ударных процессов.- М.: Машиностроение, 1969.- 248с.». Но и рассмотренный пример, в котором ударная сила оказалась в 5000 раз большей веса шарика, убедительно поясняет будущему инженеру почему неотъемлемой составляющей оборудования машиностроительных заводов являются различного типа молоты и ковочные машины, объясняет причину присутствия практически в каждом доме обыкновенного молотка. Но ... продолжим иллюстрацию применимости закона об изменении количества движения рассмотрением ещё одного примера, также на ударное явление, но в ином аспекте.

Рассмотрение примера предваряем понятием:

е

27.9

сли шарик, двигаясь по нормали к неподвижной поверхности, ударяется о неё со скоростью , а отскакивает с , то отношение называют коэффициентом восстановления скорости;

экспериментальные данные показывают, что при скоростях удара до 10 м/с коэффициенты восстановления скорости имеют следующие примерные значения:

с

Скорости шариков до

и после соударения

текло о стекло - 0,93; слоновая кость о слоновую кость - 0,88; сталь о сталь - 0,55; дерево о дерево - 0,5. Ясно, что если удар наносится по подвижному телу, то в числителе и знаменателе формулы 27.9 будут фигурировать разности между скоростями до и после удара.

ПРИМЕР 27.5.- Прямой центральный удар двух шаров

Д

Рисунок 27.2

ано. – По одной прямой перемещается два шарика с одинаково направленными скоростями и . 1-й шарик догоняет второй (м/с). Массы шариков: г; г. После удара скорости шариков изменяются – становятся равными и (ясно, что модуль скорости становится меньшим модуля скорости ).

Требуется.- Считая известным коэффициент восстановления скоростей

а

,

определить модули и скоростей шариков после их соударения.

Решение.- Принимаем к рассмотрению систему, состоящую из обоих шариков.

Для неё

217

б

где - количество движения системы из 2-х шариков после удара и до него; - импульсы сил тяжести и нормальных реакций. Замечание: ударные силы являются внутренними и, поэтому, в уравнении не учитываются.

Спроектировав векторное равенство (б) на направление скоростей, получаем:

в

.

Для определения неизвестных и решаем систему алгебраических уравнений (а) и (в):

Чтобы избавится от неизвестной первое уравнение умножаем на (-), второе на “1” , полученные уравнения складываем и т.д. ... после алгебраических преобразований получаем:

. .

После подстановки заданных численных значений определяем: м/с; м/с .

2

К постановке вопроса о равновесии оболочки с текучей средой

7.6. Условие равновесия оболочки с ответвлениями и установившимся в ней движением текучей среды

На рис.27.3 изображена механическая система, оконтуривающую оболочку которой в нескольких местах пронизывают потоки текучей среды (обычно жидкость). По одним частицы втекают внутрь оболочки, по другим вытекают. Потоки характеризуют

секундные массы

а

т

Рисунок 27..3

.е. это протекающие через поперечные сечения потоков за единицу времени массы

текучей среды;

218

1, 2, ... , i, ... , N - номера потоков текучей среды; - средние по поперечным их сечениям скорости частиц.

Пусть оболочка имеет неизменяемую форму и неподвижна относительно инерциальной системы отсчёта, а - действующий на неё главный вектор внешних сил.

Принимаем к рассмотрению совокупность частиц, которая в момент времени расположена внутри оболочки. Количество её движения -.

Локальная аксиома (о постоянстве содержащегося в оболочке количества движения):

П

27.10

ри установившемся движении текучей среды, протекающей через оболочку с ответвлениями, содержащееся в ней количество движения является постоянной во времени величиной.

У

27.11

становившимся называется такое движение текучей среды, при котором .

П

К выводу условия равновесия оболочки

с текучей средой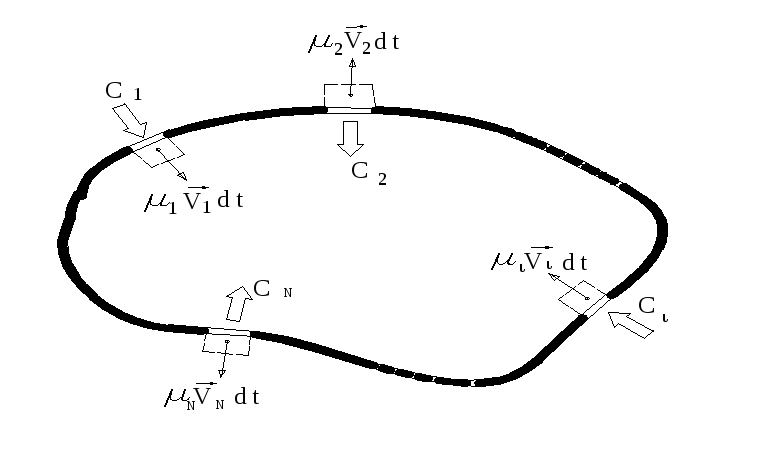

ринятая к рассмотрению для момента временимеханическая система к моменту изменит свою форму – на рис.4 эти изменения отображены 4-мя прямоугольниками (но мысленно представляется не 4, а прямоугольников - -ый; кроме того, в направлении скоростей размеры таких прямо-угольников – бесконечно малые величины - определяемые произведениями ).

Р

Рисунок 27.4

ис.4 помогает увидеть, что в момент времени количество движения принятой к рассмотрению механической системы определяется выражением:

.

Откуда:

.

Учитывая 27.5, т.е. учитывая, что , из последнего выражения получаем:

219

.

Векторы , которые параллельны соответствующим векторам скоростей , направлены внутрь оболочки и модули которых вычисляются по формулам, называемнаправленными внутрь оболочки секундными количествами движения потоков текучей среды. Тогда последнее выражение принимает вид:

.

Итак, получено

условие равновесия оболочки с ответвлениями при уста-

новившемся режиме движения протекающей в ней текучей среды:

- для оболочки с ответвлениями при установившемся движении в ней текучей среды главный вектор всех внешних сил и секундных количеств движения, направленных внутрь объёма, равны нулю.

Замечание.- Определение направления движения потоков не является предметом теоретической механики. Это рассматривается в гидравлике. Но подчёркиваем: секундные количества движения следует направлять внутрь оболочки, независимо от того втекающим или вытекающим является поток.

Результат 27.11 применительно к оболочке с одним входом и одним выходом известен как хорошо проверенное жизнью уравнение Эйлера об изменении секундного количества движения жидкости.