у

35.1

словия равновесия консервативных систем:

.

35.3. Понятие об устойчивости равновесия

Примеры устойчивого и неустойчивого равновесия

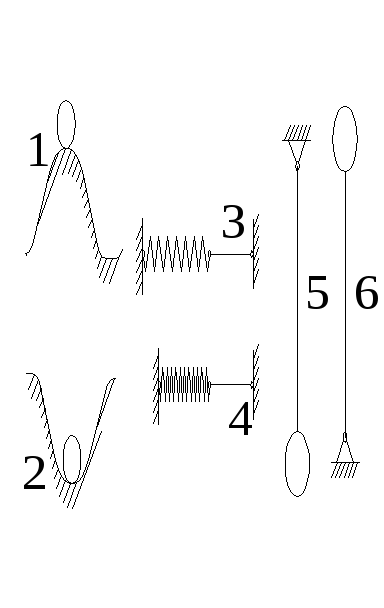
Рисунок 35.1

На рис.35.1: 1 и 2 – мяч на бугорке, и в ямке; 3 и 4 – шарнирное соединение стержня с растянутой, и сжатой пружиной; 5 и 6 – стержень с шариком на конце шарнирно соединённый с потолком, и полом.

Полагаем, что читатель самостоятельно решит, где положение равновесия устойчиво, где неустойчиво.

Но если бы было всё так просто, создавать теорию устойчивости не требовалось бы. Через подраздел будет приведен пример, в котором устойчивость (либо неустойчивость) равновесия не очевидны.

Сейчас же дадим общее понятие:

р

35.2

35.4

авновесие называют устойчивым, если система после её отклонения (или после придания небольшой начальной скорости) начинает колебаться около своего начального положения, а затем (после затухания колебаний) возвращается в исходное положение.

13.4. Основные результаты общетеоретических исследований устойчивости равновесия механических систем

З

35.3а

акон устойчивости равновесия консервативных систем:

положение равновесия консервативной системы устойчиво, если её потенциальная энергия в этом положении имеет строгий минимум.

Напоминание: понятие «строгий минимум» (синонимы: «изолированный минимум», при двух степенях свободы – «потенциальная яма») применимо к системам с несколькими степенями свободы – это минимум функции по всем обобщённым координатам.

329

Рассматриваемый подраздел является ещё одним примером, иллюстрирующим ранее высказывавшееся мнение о том, что настоящие теории

- это плод учёных многих поколений и стран.

Ещё Торричелли, основываясь на результатах, корни которых теряются в глубокой древности (добавляя, естественно, и своё), давал правильные результаты применительно к механическим системам, на которые действуют силы тяжести. В частности, он писал: «Два связанных друг с другом тяжёлых тела не могут сами собой двигаться, если их центры тяжести не опускаются».

Сформулировал результат 35.3а, в виде теоремы, Лагранж, но доказал её Дирихле. Томсон расширил результат 35.3а:

35.3б

равновесие, устойчивое при одних потенциальных силах, сохраняет устойчивость при добавлении гироскопических и диссипативных сил.

Гироскопические силы – это те, работа которых на действительном перемещении всегда равна нулю.

Диссипативные силы – это силы, приводящие к рассеиванию энергии; обычно – это силы трения.

Возникает вопрос об обратимости результата 35.3: «Можно ли утверждать, что при отсутствии строгого минимума потенциальной энергии равновесие будет неустойчивым»? Впервые такой вопрос был поставлен Ляпуновым. И частично на него он ответил сам – двумя теоремами. Затем это было расширено ещё теоремами Н.Четаева и Н.Красовского. И всё же полного ответа на поставленный Ляпуновым вопрос до сих пор нет. Более того, имеются примеры устойчивого равновесия и при отсутствии строгого минимума (см., например, с.195 в книге «Гантмахер Ф.Р. Лекции по аналитической механике.- М.: Наука, 1966.- 300 с.»).

Но инженер действует конкретно, с ответственностью за принимаемые решения, но к сожалению не может ждать появления исчерпывающего ответа на сформулированный Ляпуновым вопрос. Поэтому рекомендация:

если для положения равновесия минимум потенциальной энергии не установлен, принимайте это положение за неустойчивое, считая, что вероятность возможной ошибки не превысит (ориентировочно) 1%.