34.3.2. Понятие об обобщённых силах.

Уравнения динамического равновесия в обобщённых силах

В

34.6

разделе 32 получено уравнение возможных работ:

.

Оно справедливо для любого возможного перемещения системы. Но для решения конкретных задач все возможные перемещения не нужны. Нужны лишь в количестве, обеспечивающем составление максимума независимых друг от друга уравнений, а их (- число степеней свободы механической системы). Причём, нужны такие возможные перемещения, при которых алгебраические преобразования сводятся до минимума. А там же (в разделе 32) было показано, что простота достигается одиночными вариациями обобщённых координат.

В развёрнутом виде эти простейшие, в количестве , уравнения предстают в виде столбца уравнений изстрок, с соответствующими нижними индексами, а в свёрнутом виде:.

319

Делим левую и правую части записанного уравнения на вариацию -той обобщённой координаты (на). Получающиеся отношения называют:--тая внешняя обобщённая сила;--тая внутренняя обобщённая сила;--тая обобщённая сила инерции.

Итак, получены

уравнения возможных работ и мощностей в обобщённых силах -

б

.

3. Рекомендация по вычислению обобщённых сил

, где

- возможная скорость -той точки, выраженная в долях скоростиодиночной вариации-той обобщённой координаты (или – передаточное отношение от-той обобщённой координаты к-тому объекту механической системы – частице, телу). Итак,

формулы для вычисления обобщённых сил:

, где

- вектор передаточного отношения от -той обобщённой коор-динаты к-той точке.

Т.к. результат не зависит от скорости вариации обобщённой координаты (см. раздел 32), то при конкретных расчётах скорости вариаций обобщёнными координатами () можно принимать равными единице (делить на единицу всегда проще), например 1 м/с.

34.3.4 Три математические зависимости, используемые

в непосредственном выводе уравнений Лагранжа 2-го рода

Действительная скорость -той частицы:

применяем правило взятия производной функции многих переменных =

Т.к.

320

, то в записанных частных от него производных не могут появиться обобщённые скорости. Поэтому:

в

.

Из множества возможных движений частиц принимаем подмножество, описываемое выражением:

,

которое в свою очередь, сужаем до - ограничиваемся одиночными вариациями обобщённых координат. Тогда:

и при , о допустимости чего уже говорилось, получаем:

г

.

Для третьей математической зависимости используем правило взятия производной от произведения двух функций:

д

.

34.3.5. Непосредственный вывод уравнений Лагранжа 2-го рода

Начинаем с (б):

учитываем (д)=

, где:

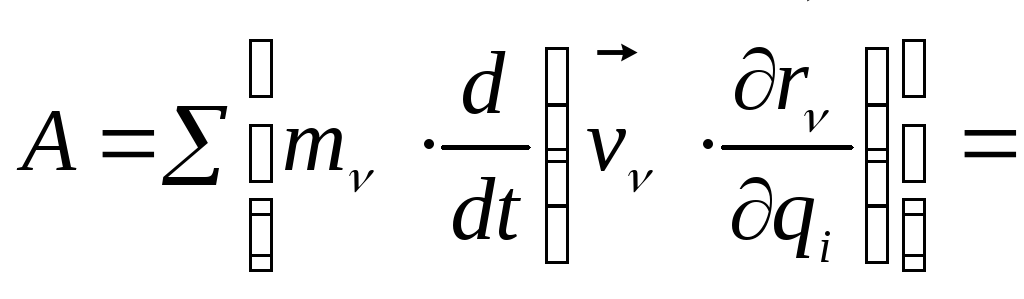
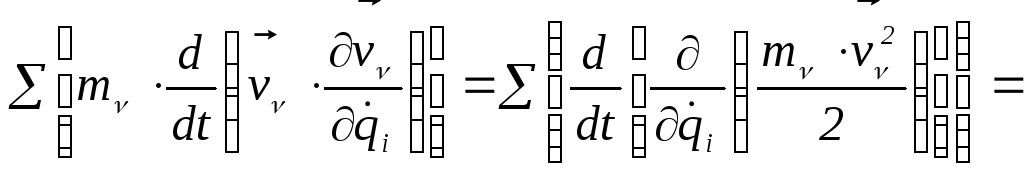
321

;

а

.

Итак, получены

уравнения Лагранжа 2-го рода:

34.7

.

З

К примеру 34.1 - на уравне-нения Лагранжа 2-го рода

амечание: для механических систем с идеальными связями, что часто принимается в практике расчётов (с целью преодоления проблем, возникающих при учёте внутренних сил),.

П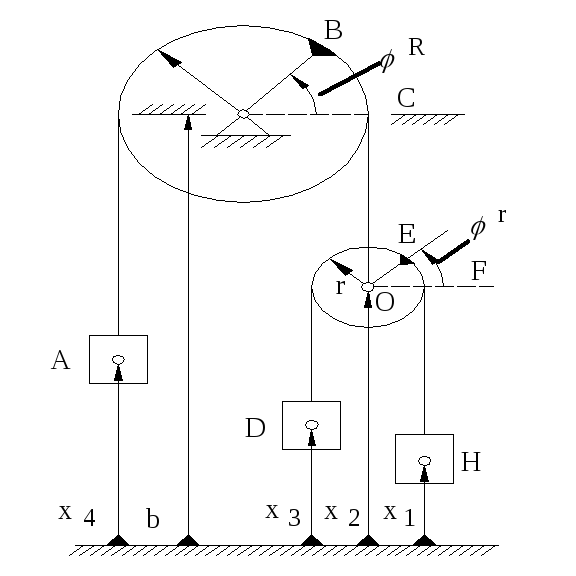РИМЕР 34.1.-Двухтросовая система, с тремя грузами, неподвижным и подвижным шкивами

Д

Рисунок 34.2

ано. – На рис.34.2: - координаты, определяющие положения тел . Их массы: кг; кг; кг; кг. Ось вращения подвижного шкива (радиуса м и имеющего жёлоб под нерастяжимый трос ) соединена с грузом также нерастяжимым тросом , который переброшен через шкив (с неподвижной осью вращения и жёлобом под этот трос; его радиус м). Угловые положения шкивов определяются переменными - подвиж-ного и - неподвижного шкивов. -

322

подвижная горизонталь. Моменты инерции шкивов: кгм²; кгм².

Требуется.- Определить ускорения всех тел.

Решение.- Положение системы определяется 6-ю координатами. Записываем уравнения связей и из них, взяв производные, устанавливаем связи между скоростями и ускорениями:

,

;

б

,

;

в

,

;

г

,

.

Видим, что шесть координат связаны между собою 4-мя уравнениями. Поэтому число степеней свободы рассматриваемой системы равно двум.

За обобщённые координаты принимаем .

Находим выражение кинетической энергии через обобщённые скорости:

34.8

Видим, что .

Теперь находим выражения частных производных от кинетической энергии по обобщённым скоростям:

323

;

а

.

Итак, .

Теперь вычисляем обобщённые силы.

Скорость вариации 1-й обобщённой координаты принимаем сонаправленной с и по модулю равной 1. Тогда

.

Рекомендация:

чтобы не запутываться со знаками (плюс или минус) скорости вариаций обобщённых координат направляйте в сторону положительного отсчёта самих координат.

Скорость вариации 2-й обобщённой координаты принимаем сонаправленной с и по модулю также равной 1. Тогда

.

Итак, составлена система 2-х уравнений:

.

Из которых:

м/с²; м/с².

Из (а) - (г): м/с²; м/с²;

; .

324