12.12. Понятие о главном моменте. Аналитический способ его вычисления

С математической точки зрения рассматриваемое понятие тождественно изложенному в подразделе 8 (где рассматривалось понятие «главный вектор»).

Пусть имеем систему из сил -. и пусть- радиус-векторы, определяющие положение точек приложения этих сил в произвольной правой системе координат.

Величину , определяемую из выражения

12.14

называют «главным моментом заданной системы сил относительно центра О».

Величины , подчинённые условию

12.15,

34

называют «главными моментами заданной системы сил относительно осей соответственно ».

Из 12.8, 12.12, 12.14и 12.15видим, что

12.16, где

- моменты сил заданной системы () относительно осей соответственно.

ПРИМЕР 12.2. - На вычисление главного момента (аналитическим методом)

Дано: проекции сили координаты точек их приложения определяются из приводимой таблицы

X, н	Y, н	Z, н	x, м	y, м	z, м
0	100	-60	1,0	0,0	0,0
100	80	0	0,8	-0,5	0,0
50	0	80	0,5	0,6	1,0
-40	0	0	0,4	0,0	-0,8

Требуется:определить главный момент заданной системы сил относительно начала координат (который обозначим точкой О).

Решение.

Нм.

Аналогично

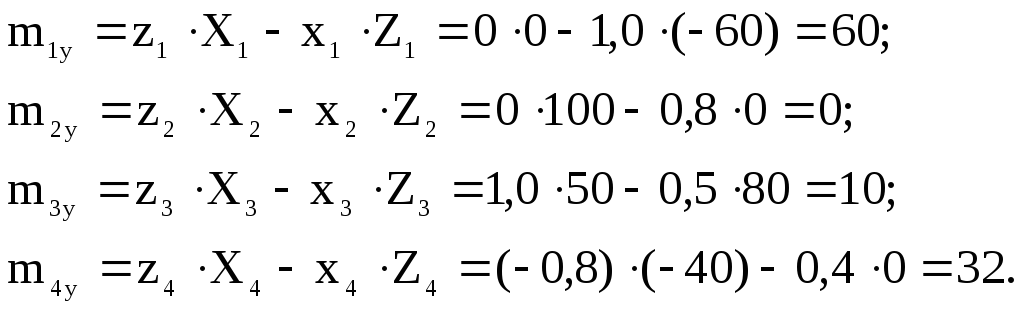
35

Нм.

Нм.

Итак, главный момент заданной системы сил:

Его модуль:

Нм.

Направляющие косинусы главного момента:

.

1 К выводу зависимости 12.172.13. Зависимость между главными моментами относительно различных центров

Эта зависимость определяется правилами векторной алгебры. На рис.10: О – некий базовый центр (например – начало системы); А – произвольно взятый другой (новый) центр.

В

Рисунок 12.10

соответствии с правилами векторной алгебры и ранее принятыми понятиями для произвольной системы силполучаем:

Итак:

36

-

г

12.17

лавный момент произвольной системы сил относительно любого центра А больше главного момента этой же системы относительно ранее взятого центра О на величину, равную векторному произведению радиус-вектора, проведенного из нового центра в старый, на главный вектор.Следствие:

у

12.18

системы сил с нулевым главным вектором главный момент не зависит от положения центра (относительно которого он вычисляется).

В

Рисунок 12.12

Рисунок 12.13

математических записях рассмотренного подраздела пределы суммирования (от=1 до=n) при символах опускались. С целью сокращения записей это часто при изложении курса будет делаться и в дальнейшем.

12.14. Понятия о противоположных силах, паре сил и её моменте, о силовом винте

Д

12.19

ве силы называютпротивоположными, если они расположены на одной прямой (говорят – «на одной линии действия»), направлены в разные стороны и равны по модулям.

П

12.20

ара сил(кратко: пара) – это совокупность двух противоположно направленных сил, линии действия которых не совпадают (см. рис.11).

К понятиям «пара» и «вектор-момент пары»

Плечо пары (h)– это кратчайшее расстояние между линиями действия сил.

В

Рисунок 12.11

ектор-момент пары сил (кратко:момент пары) - это свободный вектор с модулем равным произведению модуля силы на плечо пары () и который перпендикулярен плоскости действия пары, причём направлен так, чтобы глядя ему навстречу можно было видеть пару сил стремящейся повернуть тело (к которому она приложена) против хода часовой стрелки.

С

12.21

иловой винт(кратко –«винт»; иногда называют «динамическим винтом») - это совокупность трёх сил (рис.12.12 и 12.13), две из которых образуют пару, а третья перпендикулярна плоскости её действия.

37

К понятию «силовой винт»

Представление силового винта двумя векторами

Называют:

момент винта- это момент, создаваемый парой сил винта;

сила винта- это сила, расположенная перпендикулярно плоскости действия пары силового винта;

ось силового винта - это линия действия силы винта –

(кратко: ось винта).

38