
- •К у р с
- •С о д е р ж а н и е Введение
- •4. О важности теоретической механики и главной цели, .......................... 13 преследовавшейся авторами при построении данного «Курса»
- •Раздел I. Статика
- •12. Основные количественные характеристики механических ............ 25 действий и связи между ними
- •Раздел II.Кинематика
- •Раздел III. Динамика
- •В в е д е н и е
- •1. О предмете изучения
- •2. Об уровне совершенства и опытно-экспериментальной обоснованности теоретической механики
- •3. Об истории развития теоретической механики
- •4. О важности теоретической механики и главной цели, преследовавшейся авторами при построении данного «Курса»
- •5. О методологии теоретической механики
- •6. О строении курса
- •7. О понятиях
- •8. Об аксиомах
- •9. О предметах доказательств
- •10. Главные учебные задачи студентов
- •Раздел I. С т а т и к а
- •11. Предмет изучения и основные задачи статики
- •12. Основные количественные характеристики механических действий и связи между ними
- •12.1. Общие сведения о рассматриваемых в разделе методах
- •12.2. Аксиома о действии
- •1 К понятию о разложении силы по двум направлениям2.3. Понятия о разложении силы и её составляющих
- •12.4. О том, как сила приспособлена к векторной алгебре
- •12.5. Понятие о проекции силы на ось
- •К понятию о проекции силы на ось
- •12.6. Алгебраическая запись силы через её проекции на оси декартовой ситемы координат
- •1 К понятию о проекции силы на плоскость2.7. Понятие о проекции силы на плоскость
- •12.8. Понятие о главном векторе. Основные способы его вычисления
- •К условию примера 12.1
- •К решению примера 12.1
- •12.9. Понятие о векторе-моменте силы
- •12.10. Моменты сил относительно осей и их связи с вектором-моментом
- •12.11. Способ перестановки индексов
- •12.12. Понятие о главном моменте. Аналитический способ его вычисления
- •1 К выводу зависимости 12.172.13. Зависимость между главными моментами относительно различных центров
- •12.14. Понятия о противоположных силах, паре сил и её моменте, о силовом винте
К решению примера 12.1



Е



го
направляющие косинусы:
![]()


![]()
Г











лавный
вектор
![]() ,
его составляющие
,
его составляющие
![]() и
и
н




аправляющие
углы
![]() изображены
изображены
на
рис.12.7.
Рисунок 12.7
31
12.9. Понятие о векторе-моменте силы
Сила – главная мера механического действия, но для описания механических явлений одной её недостаточно, что поясним конкретным примером: дверную ручку прибивают на наибольшем удалении от оси вращения двери; и если кто-либо попытается отступить от этого правила (прибив её вблизи от дверных петель) он окружающими людьми будет осмеян.
П
К понятию «вектор-момент
силы
В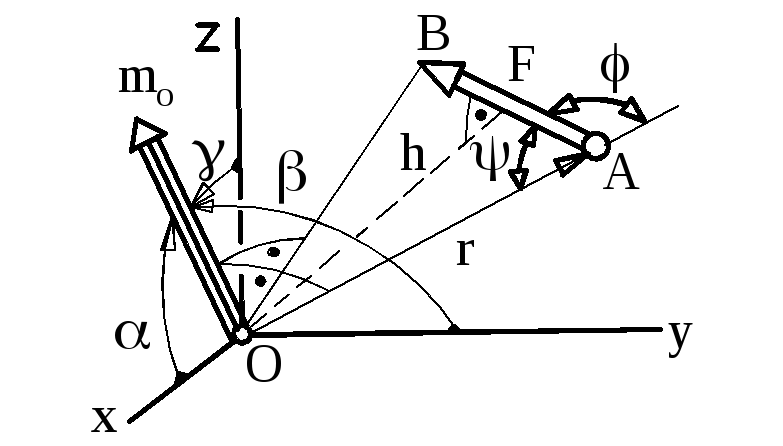 ектор-момент
силы
ектор-момент
силы
![]() относительно произвольного центра О
(рис.12.8) – это свободный
вектор
относительно произвольного центра О
(рис.12.8) – это свободный
вектор
![]() ,
равный векторному произведению
радиус-вектора
,
равный векторному произведению
радиус-вектора ![]() точки приложения даннойсилы
на саму силу
точки приложения даннойсилы
на саму силу![]() ,
т.е.
,
т.е.

12.8![]()
О
Рисунок 12.8
в
12.9 ектор-момент
(
ектор-момент
(![]() )
расположен перпендикулярно силе (
)
расположен перпендикулярно силе (![]() )
и радиус-вектору (
)
и радиус-вектору (![]() )
точки её приложения (расположен
перпендикулярно треугольнику ОАВ -
см. рис.12.8), причём направлен в ту сторону,
чтобы глядя навстречу этому вектору
видеть силу
)
точки её приложения (расположен
перпендикулярно треугольнику ОАВ -
см. рис.12.8), причём направлен в ту сторону,
чтобы глядя навстречу этому вектору
видеть силу
![]() действующей в направлении поворота
треугольника ОАВ против хода часовой
стрелки;
действующей в направлении поворота
треугольника ОАВ против хода часовой
стрелки;
м
12.10 одуль
вектора-момента (
одуль
вектора-момента (![]() )
не зависит от положения конца
радиус-вектора (
)
не зависит от положения конца
радиус-вектора (![]() )
на линии действия силы (
)
на линии действия силы (![]() )
и равен удвоенной площади треугольника
ОАВ.
)
и равен удвоенной площади треугольника
ОАВ.
И действительно, в сответствии с понятием векторного произведения
![]()
![]() .
.
12.10. Моменты сил относительно осей и их связи с вектором-моментом
Под моментом силы относительно оси понимают проекцию на эту ось её вектор-момента относительно любой точки рассматриваемой оси, т.е. моменты
32
![]() относительно осей соответственно
относительно осей соответственно
![]() - это величины (см. рис.12.8), определяемые
из соотношений
- это величины (см. рис.12.8), определяемые
из соотношений
1 2.11
2.11
![]()
![]()
![]() ,
,
где
![]() -
модуль вектора-момента силы
-
модуль вектора-момента силы![]() относительно начала системы координат
относительно начала системы координат![]() ,
а
,
а![]() ,
,![]() и
и![]() - направляющие косинусы для вектора-момента.
Итак, в соответствии
с введенными понятиями
- направляющие косинусы для вектора-момента.
Итак, в соответствии
с введенными понятиями
1 2.12
2.12![]() .
.
12.11. Способ перестановки индексов
Важность владения способом определяется большой частотой его использования (не только в статике, но в кинематике и динамике).
В правой прямоугольной системе
координат
![]() (это система координат с ортами
(это система координат с ортами![]() удовлетворяющими условию
удовлетворяющими условию![]() )
считаем известными проекции силы
)
считаем известными проекции силы![]() (
(![]() )
и радиус-вектора
)
и радиус-вектора![]() точки её приложения (
точки её приложения (![]() ).
).
В соответствии с 12.8, 12.12 и правилами векторного произведения имеем:

Откуда:
12.13а![]()


На первый взгляд кажется, что формулы 12.13а сложны для запоминания.
Процесс написания любой из трёх формул 12.13аоказывается простым, если его раскладывать на 3 этапа:
1. По исходной векторной формуле
![]()
![]() (которую надо, конечно, помнить) пишется
скалярная формула
(которую надо, конечно, помнить) пишется
скалярная формула
![]() ;
;
33
2 К способу перестановки
индексов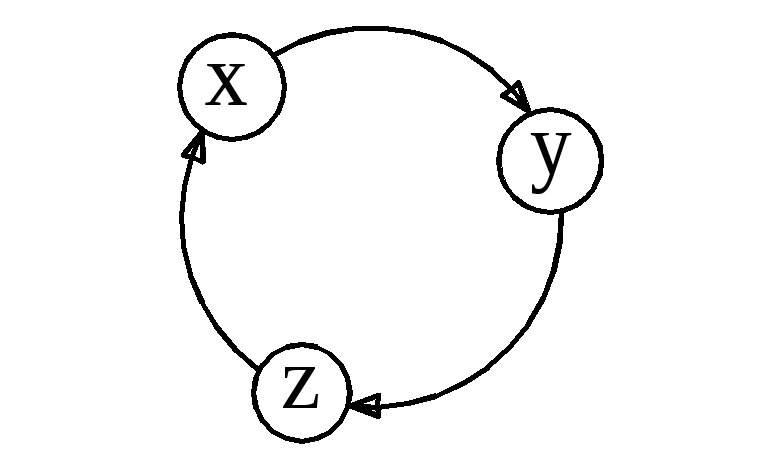
3. Вторые произведения в правых частях (стоящие после минусов) получаются из первых - путём написания тех же букв и индексов, но индексы при их привязке к буквам меняют местами.
С
Рисунок 12.9![]()
![]() ),
),
многократно в динамике и поэтому им целесообразно владеть свободно. Что значит «свободно»? Это значит любую из трёх формул 13а по команде товарища следует успевать записывать за 10 секунд.
Обычно стремятся к более простым записям.
По этой причине вместо двухбуквенных
обозначений
![]() ;
;![]() пишут однобуквенные -
пишут однобуквенные -![]() и
и![]() .
В этом случае формулы 13а принимают
вид:
.
В этом случае формулы 13а принимают
вид:
12.13б![]()


