12.5. Понятие о проекции силы на ось

Пусть - произвольная ось, - её орт, - произвольная сила. Величину

12.3

называют проекцией силы на ось .

П

К понятию о проекции силы на ось

роекция силы на ось - величина алгебраическая. На рис.3 этому понятию дано геометрическое толкование:

-

A

на картинках 3а и 3г уголрасположен в интервалах 0-90^о и 270-360^о; в этих случаях проекция силы на ось больше нуля;

когда же уголрасположен в интервале 90-270^о (картинки 3б и 3в), проекция силы на ось меньше нуля.

В

Рисунок 12.3

практике расчётов обычно оперируют острыми углами (на 4-х картинках рис.3 – углы). В этих случаях удобно пользоваться правилом:

е

12.4

сли при мысленном следовании в положительном направлении оси раньше встречается проекция начала вектора, то проекция силы на ось – величинаположительная; если раньше встретится проекция конца вектора, то проекция силы на ось – отрицательная величина.

Примеры обозначения проекций сил:

- проекции силы на оси соответственно;

- проекции силы на оси оси.

12.6. Алгебраическая запись силы через её проекции на оси декартовой ситемы координат

Если - орты осей ,то, в соответствии с2и3:

12.5

.

29

1 К понятию о проекции силы на плоскость2.7. Понятие о проекции силы на плоскость

Вектор, направление и модуль которого определяют по правилам, ясным из рис.4, называют проекцией векторана плоскостьН.

П

Рисунок 12.4

ояснения к рис.4: acиbd принадлежат плоскостиН;Aaи BKb – перпендикуляры к плоскости Н; осьAkxпараллельнаab.

12.8. Понятие о главном векторе. Основные способы его вычисления

Пусть - произвольная система сил.

Величину , определяемую из условия:

12.6

называют главным вектором рассматриваемой системы сил.

О

К графическому способу вычисления главного вектора

тдельно взятых, сгруппированных по тем или иным признакам, систем сил может быть любое количество и в общем случае речь может вестись о главном векторе 1-й, 2-й,j-той и т.д.,k-той систем сил, т.е. о.

Г

B

3

Рисунок 12.5

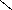
еометрическое представление понятия «главный вектор» иллюстрировано на рис.5, гдеAD,AB,BCиCD- направленные отрезки, в одном масштабе изображающие главный вектор и его составляющиеи.

Представленный на рис.5 графический способ определения главного вектора на практике целесообразно применять лишь для плоских систем сил. По причинам же универсальности и компьютеризации общества основным способом определения главного вектора следует считать аналитический. Опишем его.

Проекции сил и главного вектора на оси обозначим, соответственно,

. Тогда:

30

Но .

И

12.7

з сопоставления двух последних выражений:

.

З

К условию примера 12.1

амечание: с целью упрощения записей, что будет делаться и в дальнейшем, пределы суммирования и индексы «ν» опущены.

Переходим к рассмотрению примера.

ПРИМЕР 12.1 - На вычисление главного вектора (аналитическим способом)

Д

Рисунок 12. 6

ано: к вершинам куба приложены силы ; точки их приложения и направления указаны на рис.6, а модули равны: Н; Н; Н; Н.

Требуется: определить главный вектор заданной системы сил (модуль и направляющие косинусы).

Решение: Н.

Н.

Н.

Модуль главного вектора:

Н.