Расчет допускаемых напряжений
Допускаемое напряжение изгиба для материала конического зубчатого колеса определяем по формуле
,
где
-
предел текучести материала; принимаем
;
-коэффициент,
учитывающий температурный режим
передачи; принимаем для 60С
;
-
коэффициент, учитывающий технологию
изготовления зубчатых колес; принимаем
;
-коэффициент,
характеризующий частоту нагружений;
принимаем
;
-
коэффициент концентрации напряжений
в корне зуба; принимаем
;
-
коэффициент, зависящий от расчетного
срока службы передачи;
вычисляем
по формуле
,
Где
-
число циклов, полученное зубом
пластмассового колеса за весь срок
службы.
Определяем эквивалентное число циклов по формуле
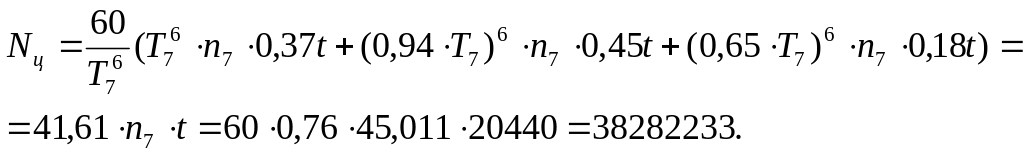
Тогда
,
Принимаем
.
Допускаемое напряжение на изгиб
.
Допускаемое контактное напряжение для материала зубчатого колеса определяем по формуле
,
где
-
предел текучести материала; принимаем
;
-коэффициент, учитывающий температурный режим передачи; принимаем для 60С ;
- коэффициент, учитывающий технологию изготовления зубчатых колес; принимаем ;
-
коэффициент, учитывающий зависимость
контактной прочности материала от
вязкости смазки; принимаем величиной
;
- коэффициент, зависящий от расчетного срока службы передачи; вычисляем по формуле
,
где - число циклов, полученное зубом пластмассового колеса за весь срок службы.
Определяем эквивалентное число циклов по формуле
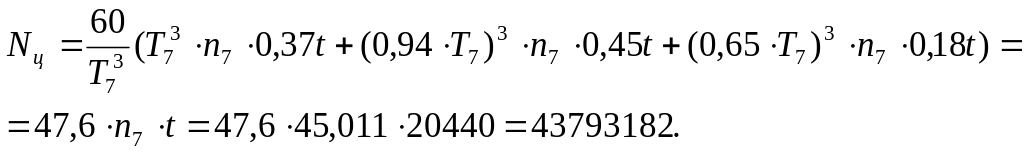
Тогда
.
Принимаем .
Допускаемое напряжение изгиба
.
Расчет геометрических размеров
Количество зубьев для шестерни рекомендуется принять 30. Количество зубьев на колесе определяется по формуле
Определяем количество зубьев шестерни и колеса:
,
.
Определяем средний модуль(мм) из условия прочности зубьев на изгиб
,
где
-коэффициент
динамической нагрузки; Принимаем
величиной
;
-
коэффициент неравномерности распределения
нагрузки по длине зуба; Принимаем
;
- коэффициент износа зубьев, принимаем
;
-коэффициент
формы зуба; зависит от эквивалентного
числа зубьев колеса
,
где
-
количество зубьев конического колеса;
-
угол при вершине конуса. Определяется
по формуле
;
.
Отсюда
.
Тогда принимаем
.
-коэффициент,
учитывающий снижение нагрузочной
способности конической передачи по
сравнению с цилиндрической; принимаем
;
U – передаточное отношение конической передачи; принимаем U=2,5.
-
количество зубьев конической шестерни;
;
-
коэффициент ширины зуба относительно
среднего диаметра шестерни; принимаем
.
Тогда
Из условия контактной прочности зубьев определяем средний делительный диаметр пластмассовой шестерни
,
где
-коэффициент
динамической нагрузки; Принимаем
величиной
;
-
коэффициент неравномерности распределения
нагрузки по длине зуба. Принимаем
;
-коэффициент,
учитывающий снижение нагрузочной
способности конической передачи по
сравнению с цилиндрической; принимаем
;
-
коэффициент, учитывающий форму сопряженных
поверхностей зубьев. Формула для
вычисления
.
-
коэффициент, учитывающий механические
свойства материалов сопряженных колес,
,
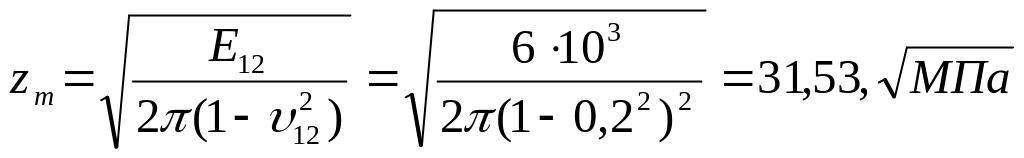где
-модуль
упругости колеса (см. табл. Механических
характеристик);
-
коэффициент Пуассона (см. табл. Механических
характеристик).
Тогда
Проверим условие
,мм.
Условие выполняется.
,мм.
Ширина зубчатого венца
.
Максимальный модуль
.
Диаметр внешней делительной окружности шестерни
,мм.
Диаметр внешней делительной окружности колеса
,мм.
Диаметр внешней делительной окружности по вершинам зубьев шестерни
,мм.
Диаметр внешней делительной окружности по вершинам зубьев колеса
,мм.
Диаметр внешней делительной окружности по впадинам зубьев шестерни
,мм.
Диаметр внешней делительной окружности по вершинам зубьев колеса
,мм.
Конусное расстояние
,мм.