10 Устойчивость нелинейных сау. Построение фазовых характеристик
В отличие от линейных систем устойчивость в нелинейных системах зависит от начальных условий, но и само понятие устойчивости для нелинейных систем требует уточнения.
Во-первых, как и в линейных системах в нелинейных возможно состояние равновесия, которому соответствует постоянное значение управляемой величины. Это состояние может быть устойчивым и неустойчивым.
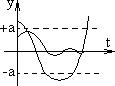
Величина а, которая является своего рода границей устойчивости по начальному условию, может быть большой и малой. В зависимости от этого различают:
1) Устойчивость «в малом», когда величина а мала.
2) Устойчивость «в большом», когда величина а большая, но конечная.
3) Устойчивость «в целом», когда величина а не ограничена.
Во-вторых, в нелинейных системах возможно установившееся состояние с периодическим изменением управляемой величины. В отличие от линейных систем это состояние также может быть устойчивым. Устойчивые периодические колебания управляемой величины при отсутствии возмущения называются автоколебаниями.
Фазовые траектории автоколебаний образуют предельный цикл, который может быть как устойчивым, так и не устойчивым.
Особенностью
реальных систем является то, что точный
вид нелинейных характеристик неизвестен,
а также они могут существенно меняться
в процессе эксплуатации, поэтому важно
гарантировать устойчивость равновесия
в целом при возможных, но не контролируемых
изменениях нелинейных характеристик.
Если устойчивость положения в целом
обеспечивается при характеристиках
нелинейного элемента удовлетворяющих
неравенству
,
то система устойчива абсолютно.
Следовательно, при выполнении условий
абсолютной устойчивости можно
гарантировать устойчивость равновесного
состояния, не имея точных нелинейных
зависимостей
Определим условия устойчивости системы, состоящей из нелинейного безинерционного звена y= F(x) и линейного звена с передаточной функцией W(p).
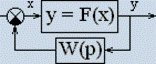
W(p) – линейная передаточная функция цепи обратной связи
F(x)
- безинерционный нелинейный блок,
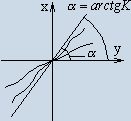
относительно которого известно, что
зависимость F(x) может иметь любое
очертание не выходящее за пределы
заданного угла
.
Для
определения устойчивости разомкнем
цепь ОС, пусть ККП линейного звена
(а)
Вначале будем считать, что вместо нелинейного устройства стоит линейный элемент с коэффициентом передачи K, тогда частотная характеристика разомкнутой системы
(б)
для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф характеристики (б) не охватывал точку (-1; j0). Иначе говоря, для устойчивости необходимо и достаточно, чтобы годограф характеристики (а) не охватывал точку (-1/к; j0).
В
общем случае при произвольном изменении
характеристики нелинейного звена
устойчивость не гарантируется. Для
абсолютной устойчивости равновесия
достаточно, чтобы на плоскости
преобразования частотной характеристики
через
точку (-1/к; 0) можно было провести такую
прямую, которая лежала бы слева от кривой
-
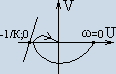
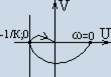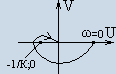
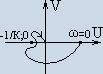устойчивые системы.
-
неустойчивые системы.
Построение фазовых характеристик.
Состояние системы n-го порядка в каждый момент времени характеризуется n-параметрами. В n-мерном пространстве это состояние отображается точкой (изображающей точкой). С течением времени составляющая системы меняется и точка перемещается, рисуя фазовую траекторию. Наиболее часто метод используется для нелинейных систем 2го порядка, тогда в фазовое пространство вырождается фазовая плоскость.
Основные закономерности фазовых траекторий:
- изображенная точка в верхней полуплоскости перемещается вправо, так как x'>0 и переменная должна возрастать, в нижней полуплоскости x'<0 и переменная должна убывать.
- фазовые траектории пересекают ось абсцисс под углом 90, т.к. на этой оси x'=0, что соответствует макс или мин самой переменной
- изображение периодического процесса является замкнутой фазовой траекторией. Образованный ими фазовый контур - цикл.
Для синусоидальных колебаний цикл имеет форму эллипса-устойчивый цикл.