8 Критерий устойчивости Михайлова. Используя этот критерий, исследуйте устойчивость сау, передаточная функция которой
Рассмотрим характеристический полином:
;подставив
в него
.
Тогда характеристический комплекс:
– содержит
только четные степени
,
включая и 0
–
нечетные
степени
.
Если
значения w
менять неправильно от 0 до
,
то вектор
своим концом описывает кривую Михайлова.
Для
устойчивости системы необходимо и
достаточно, чтобы вектор
при изменении w
от 0 до
повернулся на угол
(n
- порядок уравнения) против часовой
стрелки, не меняя направления поворота
и нигде не обращаясь в 0.
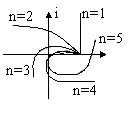
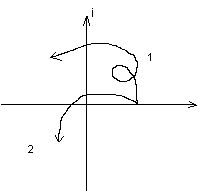
Свойства годографа Михайлова:
годограф всегда спиралевиден
при w=0 годограф начинается с точки на оси Х
при четном годограф параллельно оси Х при не четном параллельно оси У
Задача
Используя критерий Михайлова, исследуйте устойчивость САУ, передаточная функция которой .
Определим характеристический полином:
Запишем в комплексном виде:
Т.к.
,
то
Преобразуем к виду:
Получим:
Из
условия
найдем
частоту, на которой кривая пересекает
ось X.
;
Отсюда
,
или
,
т.е.
.
Получаем
координаты точек:
,
Из
условия
найдем
частоту, на которой кривая пересекает
ось Y.
Отсюда
,
т.е
Получаем
координату точки:
.
Система не устойчива, так как не проходит через 3 четверти:
9 Особенности нелинейных сау по сравнению с линейными. Линеаризация нелинейной сау
Строго линейных систем не существует. Линейная система на самом деле является линейной моделью реальной автоматической системы. Но в некоторых реальных системах возникает явлениие, необъяснимое в рамках линейной теории: зависимость характера процессов от начальных условий и внешних воздействий, существование нелинейных колебаний и другого явления. Обычно в линейной системе бывает только одно нелинейное звено, реже 2 или 3. Разновидности нелинейных звеньев:
1) Звено с релейной статической характеристикой.
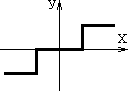
2) Звено со статической характеристикой кусочно-линейного типа.
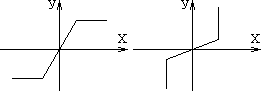
3) Звено с криволинейной статической хар-кой.
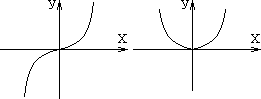
4) Звено, дифференциальное уравнение которого нелинейно за счет входящих в него произведений переменных или их производных.
5)Звено, работа которого связана с выполнением логических операций.
Нелинейности делятся на:
- сопутствующие (неизбежно присутствующие): это люфты (зазоры), трения в механических передачах, насыщения в усилителях, ограничения (механические упоры, концевые выключатели);
- преднамеренно вводимые для улучшения качественных показателей.
Специфическая особенность нелинейных систем – возникновение автоколебаний, которые существуют при отсутствии внешних воздействий (периодических) только за счет внутренних свойств систем и имеют определенную амплитуду и частоту, зависимость поведения от величины приложения воздействия, в нелинейных системах не применим принцип суперпозиции:
Метод гармонической линеаризации применим для приближенного исследования процессов в замкнутых нелинейных системах, описываемых дифференциальным уравнением любого порядка.
,
,
.
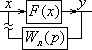
Разомкнем
систему и подадим воздействие
,
тогда на выходе будет периодический,
но в общем случае не синусоидальный
сигнал
(1).
При подаче такого сигнала на вход линейной системы на выходе всегда получается гармонический сигнал той же частоты, отличающийся только амплитудой и фазой.
Разложим (1) в ряд Фурье:
Для
нелинейных характеристик симметричных
от начала координат Со=0.
Нелинейная часть системы обычно плохо
пропускает высокие частоты, поэтому
ограничимся только первой гармоникой:
На малом интервале нелинейное ДУ можно рассматривать как линейное, но его коэффициенты зависят от амплитуды и частоты входного сигнала.
В отличие от линейных систем устойчивость в нелинейных системах зависит от начальных условий, но и само понятие устойчивости для нелинейных систем требует уточнения.
Во-первых, как и в линейных системах в нелинейных возможно состояния равновесия, которому соответствует постоянное значение управляемой величины. Это состояние может быть устойчивым и неустойчивым.
Во-вторых, в нелинейных системах возможно установившееся состояние с периодическим изменением управляемой величины. В отличие от линейных систем это состояние также может быть устойчивым. Устойчивые периодические колебания управляемой величины при отсутствии возмущения называются автоколебаниями.
Использование нелинейности для коррекции САУ
Используя линейное звено с нужной нам АЧХ его ФЧХ может нас не устраивать и наоборот. Можно создать устройство, АЧХ которого соответствует линейному звену одного вида, а ФЧХ линейному звену другого.
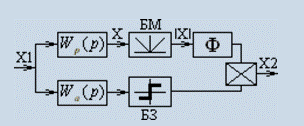
БМ-блок модуля, БЗ – блок знака, Ф-фильтр. В БМ используется выпрямитель, фильтр выделяет постоянную составляющую, нижний канал определяет фазу, БЗ исключает информацию об амплитуде, сигналы на выходе перемножаются.