2.1.2.Метод аппроксимации данных

Часто проводники межсоединений находятся в слоистой диэлектрической среде над плоскостью земли. Частный случай, когда первым (от плоскости земли) слоем является воздушный зазор, вторым – подложка с проводником, а третьим – воздушная внешняя среда, даёт два типа межсоединений: подвешенную микрополосковую линию (ПМПЛ) и обращённую микрополосковую линию (ОМПЛ) (рис.  2 .3 а,б, где h₁ – толщина воздушного зазора, h₂ – толщина подложки, _r – относительная диэлектрическая проницаемость подложки, а w – ширина полоски).

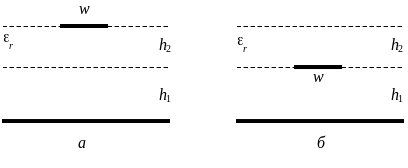
Рис. Рисунок 2.3. Подвешенная (а) и обращённая (б) микрополосковые линии

Этот частный случай важен на практике, так как он позволяет существенно уменьшить значение постоянной распространения, а также её дисперсию. Благодаря этому достоинству, он широко применяется в СВЧ линиях передачи, а квазистатические модели для этого случая применимы вплоть до 100 ГГц. Последнее обстоятельство стимулировало ряд исследований, результаты которых позволяют с достаточной для практики точностью решать задачи анализа и синтеза параметров соответствующих линий со скоростью вычислений, приемлемой для применения в САПР.

Результаты точных вычислений характеристического импеданса Z₀ и эффективной диэлектрической постоянной _re, полученные с помощью численного интегрирования по алгоритму из работы [¹³], первоначально были аппроксимированы довольно простыми аналитическими выражениями [¹⁴], которые позволили получить аналитические формулы для вычисления чувствительности характеристик [¹⁵]. Позднее, с помощью степенных полиномов были получены более точные формулы с более широким диапазоном параметров линий, как для анализа, так и для синтеза [¹⁶]. Значения ошибок соответствия полученных формул точным теоретическим данным и соответствующие диапазоны исходных параметров конфигурации приведены в табл. 2.1.

Таблица 2.2

Точность метода аппроксимации данных

Точность аппроксимации	Диапазоны параметров конфигурации
Анализ – 1% [Error: Reference source not found]	1 < w/h1 < 8	0,2 < h2/h1 < 1	r < 3,8
Анализ – 0,6%, синтез – 1% [Error: Reference source not found]	0,5 < w/h1 < 10	0,05 < h2/h1 < 1,5	r < 20

Исходные теоретические данные были получены для t=5 мкм, где t – толщина полоски. По утверждению авторов [Error: Reference source not found], для диапазона 0<t/h₁<0,02 значение изменяется в пределах 1%, а Z₀ – в пределах 2,5%. Ниже приводятся формулы для анализа и синтеза одиночных ПМПЛ и ОМПЛ [Error: Reference source not found], но следует помнить, что они применимы только в ограниченном диапазоне геометрических параметров и диэлектрических проницаемостей. В других случаях необходимо обращаться к методу, которым были получены данные для аппроксимации, или к более общим методам.

Анализ ПМПЛ

, где

,

, где	(2.0)
, где при	(2.0)

d₀₀=(176,2576–43,1240f +13,4094f ²–1,7010f ³)10^–2,

d₀₁=(4665,2320–1790,4000f +291,5858f ²–8,0888f ³)10^–4,

d₀₂=(–3025,5070–141,9368f –3099,4700f ²+777,6151f ³)10^–6,

d₀₃=(2481,5690+1430,3860f +10095,5500f ²–2599,1320f ³)10^–8,

d₁₀=(–1410,2050+149,9293f +198,2892f ²–32,1679f ³)10^–4,

d₁₁=(2548,7910+1531,9310f –1027,5200f ²+138,4192f ³)10^–4,

d₁₂=(999,3135–4036,7910f +1762,4120f ²–298,0241f ³)10^–6,

d₁₃=(–1983,7890+8523,9290f –5235,4600f ²+1145,7880f ³)10^–8,

d₂₀=(1954,0720+333,3873f –700,7473f ²+121,3212f ³)10^–5,

d₂₁=(–3931,0900–1890,7190f +1912,2660f ²–319,6794f ³)10^–5,

d₂₂=(–532,1326+7274,7210f –4955,7380f ²+941,4134f ³)10^–7,

d₂₃=(138,2037–1412,4270f +1184,2700f ²–270,0047f ³)10^–8,

d₃₀=(–983,4028–255,1229f +455,8729f ²–83,9468f ³)10^–6,

d₃₁=(1956,3170+779,9975f –995,9494f ²+183,1957f ³)10^–6,

d₃₂=(62,8550–3462,5000f +2909,9230f ²–614,7068f ³)10^–8,

d₃₃=(–35,2531+601,0291f –643,01814f ²+161,2689f ³)10^–9.

Зная , вычисляем импеданс Z по известной формуле:

,

где Z₀ – импеданс той же линии с воздушным заполнением равен

, где

,

.

(2.0)

Анализ ОМПЛ

, где

,

а f₂ вычисляется по ( 2 .0) и ( 2 .0), где

d₀₀=(2359,4010–97,1644f –5,7706f ²+11,4112f ³)10^–3,

d₀₁=(4855,9472–3408,5207f +15296,7300f ²–2418,1785f ³)10^–5,

d₀₂=(1763,3400+961,0481f –2089,2800f ²+375,8805f ³)10^–5,

d₀₃=(–556,0909–268,6165f +623,7094f ²–119,1402f ³)10^–6,

d₁₀=(219,0660–253,0864f +208,7469f ²–27,3285f ³)10^–3,

d₁₁=(915,5589+338,4033f –253,2933f ²+40,4745f ³)10^–3,

d₁₂=(–1957,3790–1170,9360f +1480,8570f ²–347,6403f ³)10^–5,

d₁₃=(486,7425+279,8323f –431,3625f ²+108,8240f ³)10^–6,

d₂₀=(5602,7670+4403,3560f –4517,0340f ²+743,2717f ³)10^–5,

d₂₁=(–2823,4810–1562,7820f +3646,1500f ²–823,4223f ³)10^–5,

d₂₂=(253,8930+158,5529f –3235,4850f ²+919,3661f ³)10^–6,

d₂₃=(–147,0235+62,4342f +887,5211f ²–270,7555f ³)10^–7,

d₃₀=(–3170,2100–1931,8520f +2715,3270f ²–519,3420f ³)10^–6,

d₃₁=(596,3251+188,1409f –1741,4770f ²+465,6756f ³)10^–6,

d₃₂=(124,9655+577,5381f +1366,4530f ²–481,1300f ³)10^–7,

d₃₃=(–530,2099–2666,3520f –3220,0960f ²+1324,4990f ³)10^–9.

Импеданс ОМПЛ вычисляется также, как и ПМПЛ, но при h₂=0.

Синтез ПМПЛ

При синтезе надо найти w/h₁ при заданных _r, h₂/h₁ и Z. Аппроксимация выражения ( 2 .0) выражением f(u)=6 даёт возможность синтеза.

Делая подстановку

,

(2.0)

получаем

,

(2.0)

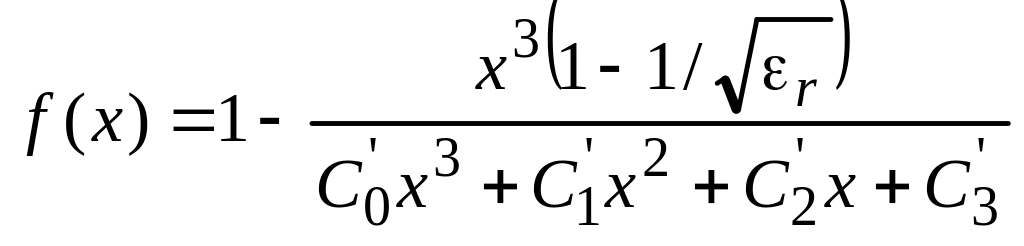где

, где

.

Синтез ОМПЛ

Делая подстановку

,

(2.0)

получаем

, где

(2.0)

.

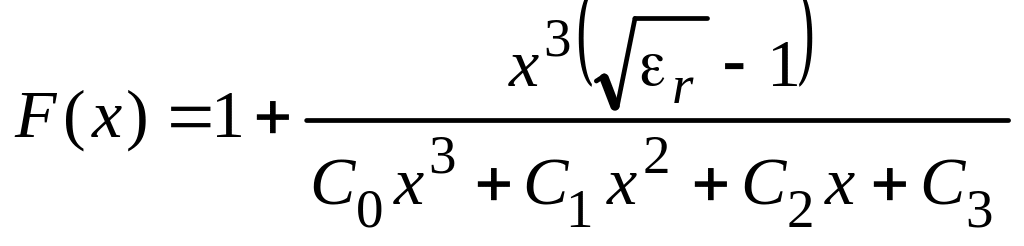Как ( 2 .0), так и ( 2 .0) можно решить с помощью любого из известных методов для определения нулей трансцендентных функций. Например, применение процедуры Ньютона-Рафсона с точкой начального приближения

, где

приводит к желаемому решению за несколько итераций. Зная x, можно вычислить w/h₁ по ( 2 .0) или ( 2 .0), в зависимости от типа линии.