2.2.Вычисление временного отклика

Вычисление отклика произвольной схемы МПЛП весьма сложно и выполняется только по алгоритмическим моделям, например [²⁷, ²⁸]. Для более простых структур, например, последовательно соединённых отрезков одиночных или двух связанных линий передачи, возможно получение эффективных аналитических моделей.

2.2.1.Аналитическая модель

Одна из простейших структур – последовательно соединенные входная линия передачи с адмиттансом Y₀ (адмиттанс – величина обратная характеристическому импедансу, а здесь – волновому сопротивлению линии), отрезок линии передачи с адмиттансом Y₁ и временем задержки ₁ и выходная линия передачи с адмиттансом Y₂. Входная и выходная линии полагаются согласованными и могут интерпретироваться как соответствующие оконечные нагрузки отрезка (рис.  2 .9).

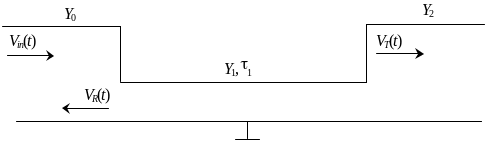
Рис. Рисунок 2.9. Эквивалентная схема отрезка линии передачи с оконечными нагрузками

Опишем сигналы на концах отрезка во временной области, используя коэффициенты передачи и отражения, входной сигнал V_in(t). Тогда, с учётом коэффициентов передачи и отражения в начале и конце отрезка, получим:  – составляющая отклика на дальнем конце структуры, учитывающая проходящую волну;  – составляющая отклика на ближнем конце структуры, учитывающая отражение от начала отрезка линии передачи;  – составляющая отклика на ближнем конце структуры, учитывающая отражение от конца отрезка линии передачи.

Следующие аналитические модели при подстановке k_ref (числа учитываемых отражений) позволяют вычислить временной отклик на дальнем конце структуры с учётом составляющих, испытавших четное число отражений, и отклик на ближнем конце структуры с учётом составляющих, испытавших нечетное число отражений,

, , где

,

2.2.2.Алгоритмическая модель

Алгоритмическая модель для вычисления временного отклика структуры из последовательно соединенных отрезков линий передачи с ёмкостями на стыках (рис.  2 .10) представлена в [²⁹].

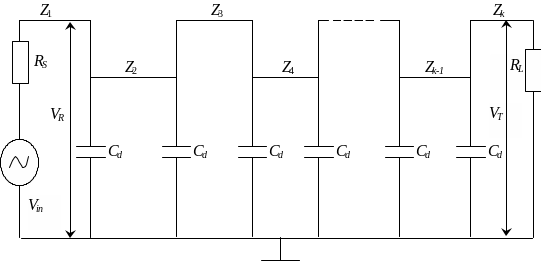
Рис. Рисунок 2.10. Эквивалентная схема структуры из последовательно соединенных отрезков одиночных и связанных линий передачи с ёмкостными нагрузками на стыках

На рис.  2 .10 применены следующие обозначения: C_d – емкость неоднородности; V_in – амплитуда напряжения гармонического сигнала с частотой ; V_R – амплитуда напряжения гармонического сигнала с частотой  в начале структуры; V_T – амплитуда напряжения гармонического сигнала с частотой  в конце структуры; Z₁, Z₂,…, Z_k-1, Z_k –волновые сопротивления отрезков; R_S, R_L – оконечные сопротивления. На рис.  2 .11 показаны направления токов , в начале и в конце отрезка i длиной D_i.

Рис.Рисунок 2.11. Направление токов , для отрезка i линии передачи

Напряжения и токи в начале и конце отрезка i в частотной области

,	(2.0)
,	(2.0)
,	(2.0)
,	(2.0)

где i – номер отрезка; D_i – длина отрезка; ; – напряжение волны, распространяющейся от начала к концу i-го отрезка; – напряжение волны, распространяющейся от конца к началу отрезка i.

Из рис.  2 .10 видно, что V_R= , а V_T= . Чтобы найти напряжение и ток в начале и конце отрезка i, необходимо найти и . Рассматривая начало структуры, можно видеть, что

,

(2.0)

где R_S – сопротивление генератора.

Подставляя ( 2 .0) и ( 2 .0) в ( 2 .0), получаем

.

(2.0)

Напряжение на конце каждого отрезка совпадает с напряжением в начале следующего отрезка, и сумма токов каждого узла равна нулю, т.е.

,	(2.0)
.	(2.0)

Подставляя ( 2 .0) и ( 2 .0) в ( 2 .0), а также ( 2 .0), ( 2 .0) и ( 2 .0) в ( 2 .0), получаем

,	(2.0)
.	(2.0)

Для оконечного сопротивления

,

(2.0)

где R_L – оконечное сопротивление, а после подстановки ( 2 .0) и ( 2 .0) в ( 2 .0)

(2.0)

Таким образом, при k отрезках из формул ( 2 .0), ( 2 .0), ( 2 .0) и ( 2 .0) получается система 2k линейных уравнений с неизвестными , ,..., и , ,..., и столбцом свободных членов V_in,0,...,0. Из преобразования Фурье от входного временного сигнала произвольной формы получают его спектральные составляющие ₁, ₂,… и их амплитуды V_in1, V_in2,…, для каждой из которых решается система уравнений ( 2 .0), ( 2 .0), ( 2 .0), ( 2 .0) и с помощью ( 2 .0) и ( 2 .0) находятся напряжения в начале и в конце структуры. Используя обратное преобразование Фурье, находятся временные отклики в начале и в конце структуры.