2. Термодинамічні політропні процеси з ідеальними газами

Задачі аналізу і загальні аналітичні залежності. Задачами аналізу є встановлення закономірностей зміни параметрів стану робочого тіла і виявлення особливостей перетворення енергії.

Враховуючи, що в ізохорному процесі і робота , вираз першого закону термодинаміки набуває вигляду:

. (2.1)

Кількість теплоти можна виразити через середню теплоємність:

. (2.2)

З (2.1) і (2.2) випливає:

, або в диференціальній формі . (2.3)

Із виразу першого закону термодинаміки для ізобарного процесу випливає:

, або . (2.4)

Кількість теплоти, виражена через середню теплоємність:

або в диференціальній формі . (2.5)

Тоді:

або . (2.6)

У диференціальній формі:

. (2.7)

Для розрахунку зміни питомої ентропії в політропному процесі використовуємо об'єднаний вираз 1-го і 2-го законів термодинаміки для оборотних процесів:

або . (2.8)

або . (2.9)

Замінивши в цих виразах і , і враховуючи, що ; , отримаємо:

; (2.10)

. (2.11)

Після інтегрування для кінцевого процесу 1-2 маємо:

. (2.12)

. (2.13)

Ізохорний процес ( ). Процес може протікати з підвищенням ( ) або зниженням ( ) тиску (рис. 2.1).

Р ис. 2.1. Графіки ізохорного процесу.

Із рівняння стану ідеального газу випливає закон Шарля:

; ; . (2.14)

Оскільки , то з рівняння 1-го закону термодинаміки випливає, що:

. (2.15)

Зміна ентропії згідно з (2.12) при

, або згідно з (2.14) . (2.16)

Оскільки , то частка теплоти, яка йде на зміну внутрішньої енергії:

. (2.17)

Оскільки , то робота в цьому процесі дорівнює нулю: .

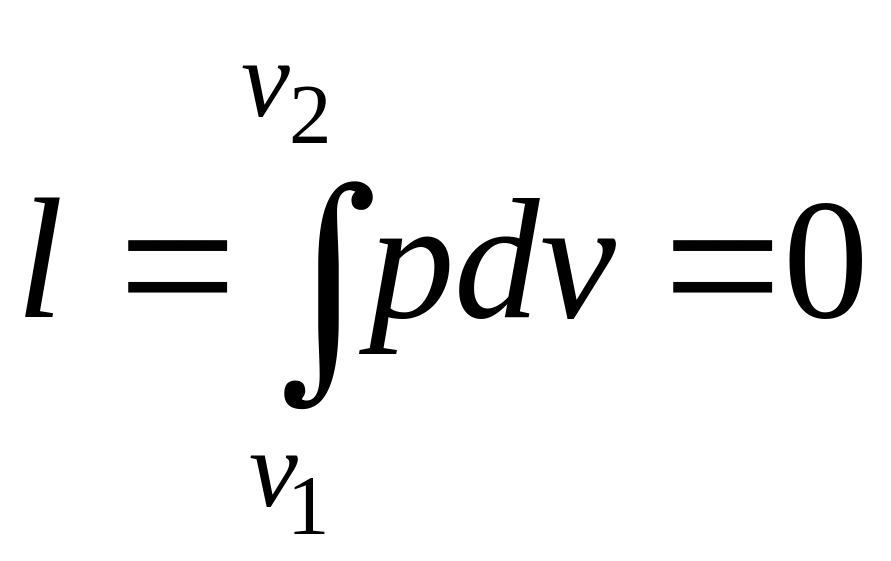Таким чином, підведена до газу в ізохорному процесі теплота цілком йде на збільшення його внутрішньої енергії.

Ізобарний процес ( ). З рівняння стану ідеального газу при (рис. 2.2) випливає закон Гей-Люссака:

; ; . (2.18)

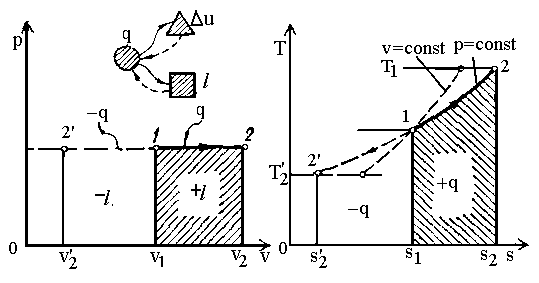
Рис.2.2. Графіки ізобарного процесу.

Робота в процесі:

. (2.19)

Оскільки для ідеального газу , то:

. (2.20)

Отже, питома газова стала R – це робота, яка виконується 1кг газу в процесі p=const при його нагріванні на один градус. Розмірність R: Дж/(кгК).

Кількість теплоти в цьому випадку, при , згідно другої форми запису рівняння першого закону :

. (2.21)

Таким чином, уся теплота, підведена до газу в ізобарному процесі, витрачається на збільшення його ентальпії.

Ця теплота для ідеального газу дорівнює:

. (2.22)

Зміна ентропії, згідно з (2.13) при :

, або, згідно з (2.18) . (2.23)

Оскільки , то ізобара в координатах більш полога логарифмічна крива, ніж ізохора.

Коефіцієнт розподілу теплоти в процесі дорівнює:

, . (2.24)

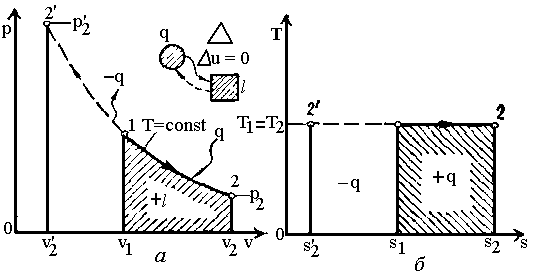
Ізотермний процес ( ). З рівняння стану ідеального газу при (рис. 2.3) витікає закон Бойля-Маріотта:

; ; ; (2.25)

Рис.2.3. Графіки ізотермного процесу.

Зміна внутрішньої енергії і ентальпії і , оскільки . Отже, вся теплота, яка підводиться, витрачається на роботу:

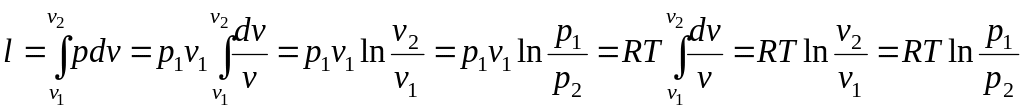. (2.26)

Теплота, необхідна для здійснення процесу:

. (2.27)

З виразів (2.26), (2.27) і (2.25) отримаємо:

. (2.28)

Частка теплоти, яка витрачається на зміну внутрішньої енергії:

. (2.29)

А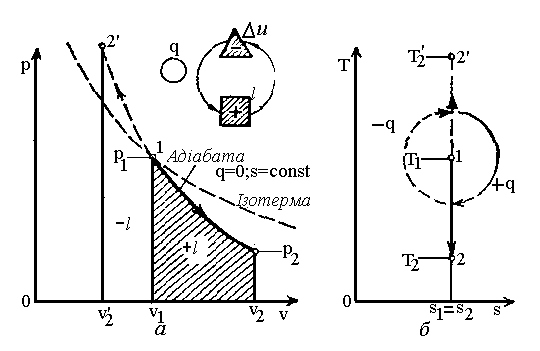 діабатний процес ( ; ) – це процес, що протікає без зовнішнього теплообміну (рис. 2.4).

Рис.2.4. Графіки адібатного процесу.

Якщо записати для цього випадку рівняння 1-го закону термодинаміки у вигляді:

чи , (2.30)

чи , (2.31)

то після ділення (2.30) на (2.31) одержимо показник адіабати:

. (2.32)

Тоді після інтегрування виразу для кінцевого процесу 1-2 будемо мати:

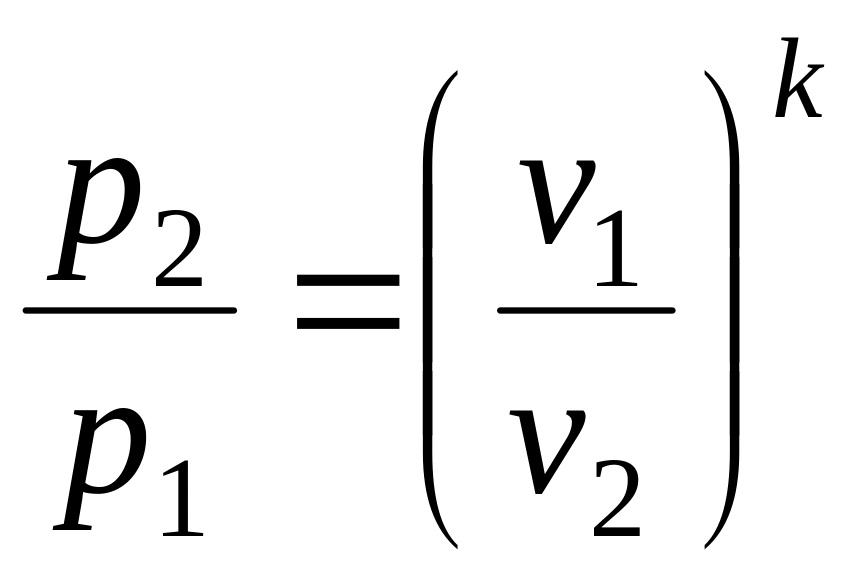, чи . (2.33)

Співвідношення між параметрами стану для двох точок в цьому процесі:

і . (2.34)

З рівняння 1-го закону термодинаміки випливає, що , тобто:

, або . (2.35)