5. Основи теплообміну

Теплопровідність (кондуктивний теплообмін). Теплопровідністю називається передача тепла від однієї частини тіла до іншої або від одного тіла до іншого, що перебувають у контакті, за допомогою молекулярного переносу (дифузії вільних електронів у металах, передачі теплового руху сусіднім молекулам і атомів в неметалах і рідинах, обміну енергією молекул, що співударяються, в газах).

Аналітичне вивчення теплопровідності зводиться до вивчення часово-просторової зміни температури у вигляді залежності:

, (5.1)

де - просторові координати в декартовій системі; - час.

Сукупність миттєвих значень температури в усіх точках досліджуваного простору називається температурним полем.

Якщо точки поля, що мають однакову температуру, з'єднати між собою, то отримаємо ізотермічну поверхню.

В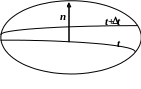 ектор, рівний першій похідній температури по нормалі до ізотермічної поверхні (рис.5.1) і спрямований у бік зростання температури називається температурним градієнтом: , К/м. (5.2)

Рис. 5.1.Температурний градієнт.

Кількість тепла, що проходить через довільну ізотермічну поверхню (F) за одиницю часу, називається тепловим потоком (Q), Дж/с. Тепловий потік, віднесений до одиниці ізотермічної поверхні, називається густиною теплового потоку (q), Вт/м²:

або у диференціальній формі . (5.3)

Густина теплового потоку є вектором, напрям якого збігається з напрямом поширення тепла і протилежний напряму вектора температурного градієнта.

Закон Фур'є. Ж. Фур'є на основі експерименту сформулював основний закон теплопровідності (закон Фур'є), згідно з яким густина теплового потоку прямо пропорційна градієнту температури, тобто:

, (5.4)

де  –коефіцієнт теплопровідності, Вт/м·К.

Коефіцієнт теплопровідності для середовищ різного агрегатного стану залежить від температури:

, (5.5)

де: - коефіцієнт теплопровідності середовища при температурі t; - коефіцієнт теплопровідності середовища при температурі t=0С; b - емпірична стала.

Диференціальне рівняння теплопровідності. Рівняння, яке описує перенос тепла теплопровідністю при наявності внутрішнього джерела (стоку) тепла називається диференціальним рівнянням теплопровідності:

або (5.6)

де - коефіцієнт температуропровідності, м²/с; q_v - потужність внутрішнього джерела (стоку) тепла Вт/м³; с_р - теплоємність при постійному тиску, кДж/кг·К;  - густина середовища, кг/м³.

Для одномірного температурного поля, наприклад, необмеженої пластини, диференціальне рівняння теплопровідності має такий вигляд:

. (5.7)

Крайові умови. Для знаходження сталих інтегрування необхідно використовувати крайові умови, які поділяють на початкову і граничні умови.

Початкова умова визначається заданням закону розподілу температури у тілі або середовищі в початковий момент часу, тобто:

. (5.8)

Граничні умови першого роду полягають у заданні температури на поверхні тіла в будь-який момент часу:

. (5.9)

Граничні умови другого роду полягають у заданні густини теплового потоку для кожної точки поверхні тіла в будь-який момент часу:

. (5.10)

Граничні умови третього роду полягають у заданні густини теплового потоку для кожної точки поверхні тіла законом Ньютона-Ріхмана конвективного теплообміну, згідно з яким кількість тепла, переданого за одиницю часу з одиниці поверхні тіла в навколишнє середовище, прямо пропорційна різниці температур між поверхнею тіла (t_п) і навколишнім середовищем (t_с):

, , , (5.11)

, . (5.12)

де  - коефіцієнт тепловіддачі (Вт/м²·К).

Стаціонарний режим. Теплопровідність плоскої стінки. Характерною ознакою стаціонарної теплопровідності є сталість у часі температури в будь-якій точці досліджуваного простору і, як наслідок, незмінність теплового потоку.

Н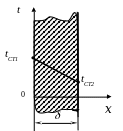 ехай маємо одношарову плоску стінку товщиною , причому її товщина значно менша лінійних розмірів бічної поверхні (рис.5.2).

Рис. 5.2. Теплопровідність одношарової плоскої стінки.

Температури на лівій і правій гранях постійні і рівні відповідно і .

Для стаціонарного процесу при відсутності внутрішніх джерел тепла в плоскій стінці рівняння теплопровідності приймає вигляд :

(5.13)

Для наведеної задачі температура (t) залежить тільки від координати х. Тому у рівнянні часткову похідну можна замінити на повну:

(5.14)

Після подвійного інтегрування цього рівняння одержуємо:

; t =C₁x+C₂ . (5.15)

Розташовуючи початок координат на лівій грані стінки, знаходимо постійні інтегрування С₁ і С₂ з умов: при х=0, t=t_CT1; при х=, t=t_CT2

С₂=t_CT1; . (5.16)

Підставляючи значення С₁ і С₂ у рішення рівняння теплопровідності, одержуємо лінійний розподіл температури в плоскій стінці:

. (5.17)

, отже: . (5.18)

Визначаючи кількість переданого тепла запишемо рівняння Фур'є:

. (5.19)

Після підстановки у рівняння Фур'є, одержимо:

, Вт/м² . (5.20)

Відношення коефіцієнта теплопровідності до товщини стінки називається тепловою провідністю плоскої стінки, а обернена їй величина, що позначається буквою R, називається термічним опором стінки, К·м/Вт:

. (5.21)

Розглянемо теплопровідність двошарової стінки з товщинами шарів ₁ і ₂ (рис.5.3). Позначимо через t_CT1 і t_CT3 температури на лівій та правій гранях двошарової стінки, а температуру на стику шарів через t_CT2.

Рис. 7.3. Теплопровідність двошарової стінки.

При стаціонарному процесі кількість тепла, що проходить через ліву і праву грані двошарової стінки, однакова. Тому кількість тепла, що пройшло через перший шар (q₁), дорівнює кількості тепла, що проходить через другий шар (q₂), тобто q₁=q₂=q= const.

Для кожної стінки можна записати:

, , (5.22)

де ₁ і ₂ - коефіцієнти теплопровідності шарів.

Додавши температурні перепади першого (t_СТ1 - t_СТ2) і другого (t_СТ2 - t_СТ3) шарів, знаходимо температурний перепад двошарової стінки:

t_СТ1- t_СТ3= . (5.23)

З отриманого виразу знаходимо тепловий потік через двошарову стінку:

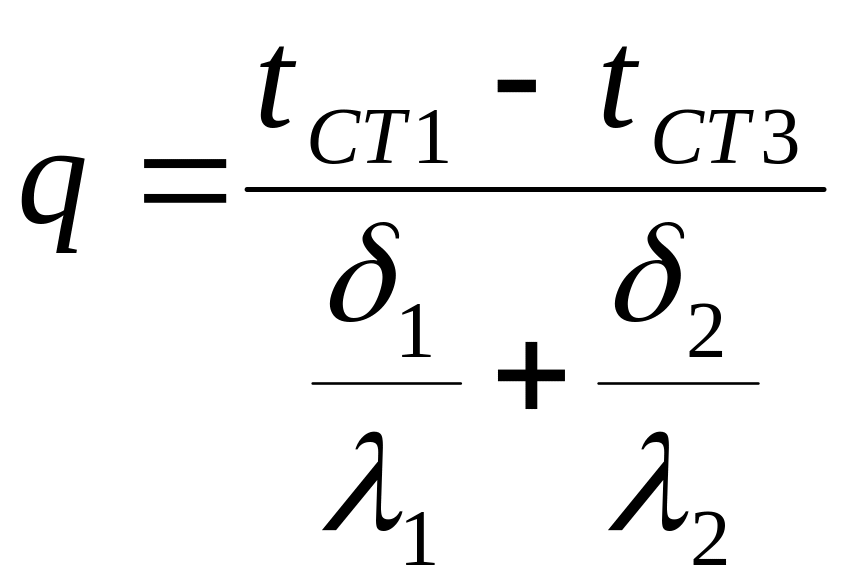. (5.24)

Аналогічно, для тришарової стінки справедливе рівняння:

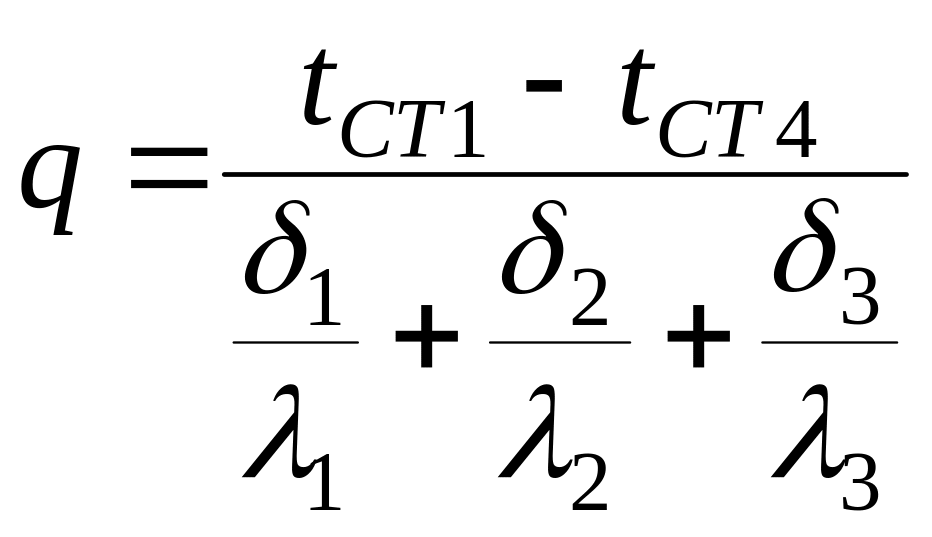. (5.25)

Для стінки, що складається з n шарів, можна записати:

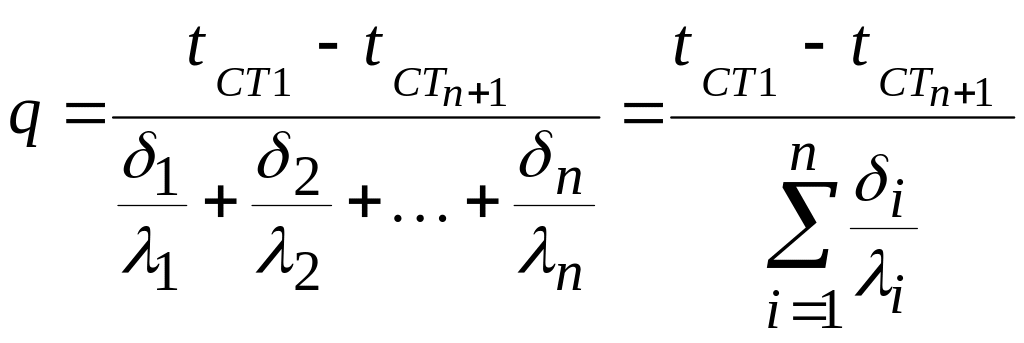, (5.26)

де – повний термічний опір багатошарової плоскої стінки.

Температура на стику першого і другого шарів дорівнює:

, (5.27)

де R₁ - термічний опір першого шару.

З останнього рівняння випливає, що:

t_СТ1- t_СТ2=q₁R₁ . (5.28)

Отже, температурний перепад кожного шару дорівнює добутку густини теплового потоку на термічний опір відповідного шару.

Еквівалентний коефіцієнт теплопровідності багатошарової стінки (_екв) дорівнює коефіцієнту теплопровідності одношарової стінки, товщина якої така ж як і товщина багатошарової, а термічний опір дорівнює термічному опору багатошарової стінки, тобто

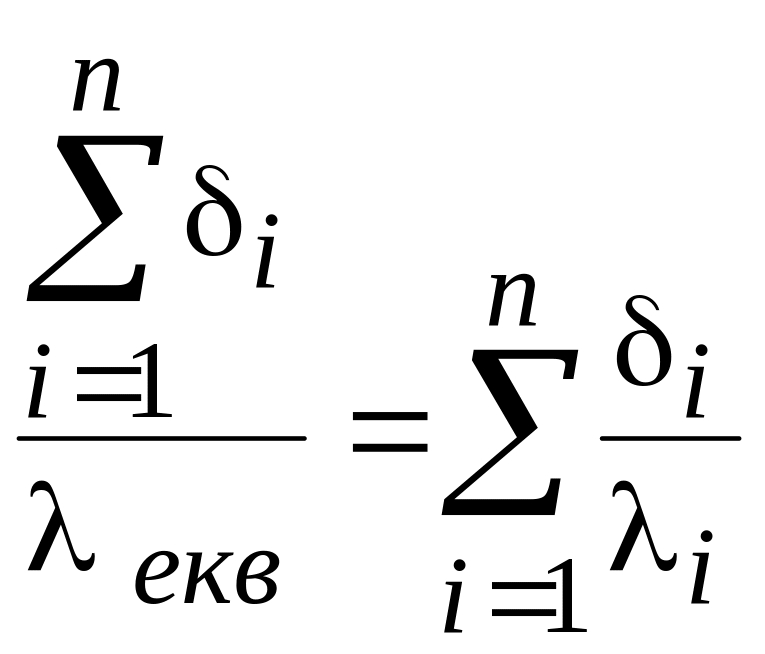, звідки 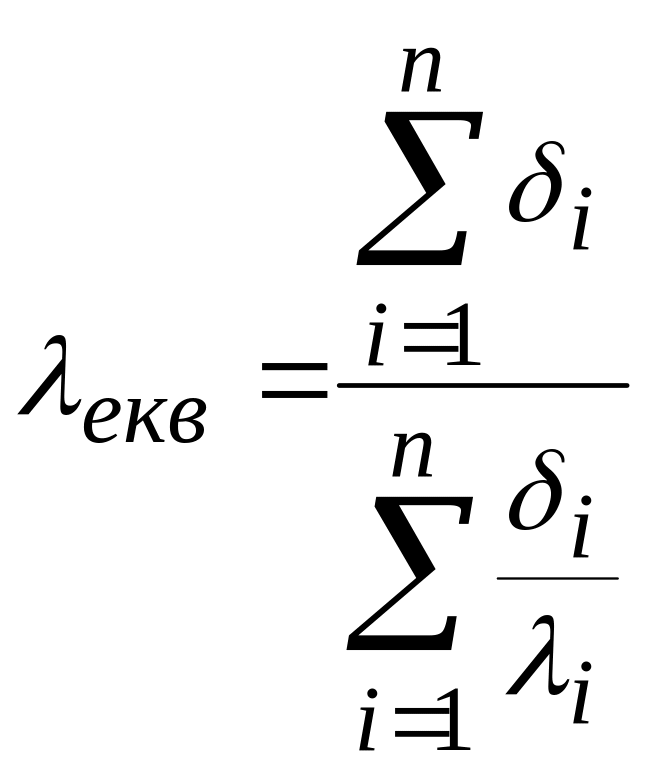. (5.29)

Тепловіддача (конвективний теплообмін). Процес конвективного теплообміну між поверхнею тіла і середовищем (рідиною або газом) описується законом Ньютона-Ріхмана або диференціальним рівнянням тепловіддачі, згідно з яким, кількість теплоти, переданої від рухомого середовища до поверхні твердого тіла і навпаки прямо пропорційна різниці температур поверхні тіла і середовища:

, (5.30)

де – площа теплообміну; – час;  - коефіцієнт тепловіддачі,Вт/м²·К; – температура поверхні тіла; – температура середовища.

Густина теплового потоку за законом Ньютона-Ріхмана:

, (5.31)

Вільна конвекція. В необмеженому просторі (рис.5.4. а):

а). Горизонтальна труба діаметром d при 10³<(Gr··Pr) <10⁸.

Nu= 0,5·(Gr·Pr)^0,25 (Pr_с/Pr_ст)^0,25 . (5.32)

б). Вертикальна труба і пластина: 1). ламінарна течія - 10³<(Gr ·Pr) <10⁹:

Nu= 0,75·(Gr·Pr)^0,25·(Pr_с/Pr_ст)^0,25 . (5.33)

2). турбулентна течія - (Gr ·Pr) > 10⁹:

Nu= 0,15· (Gr·Pr )^0,33 ·(Pr_с/Pr_ст)^0,25 . (5.34)

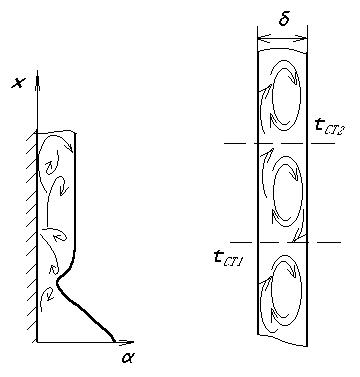
а) б)

Рис.5.4. Зміна по висоті стінки при вільній конвекції в необмеженому просторі (а) і вільна конвекція в обмеженому об’ємі (б)

Тут значення Gr, Pr і Pr_с беруться при температурі рідини (газу), а Pr_ст при температурі поверхні стінки. Визначальна температура – температура середовища; визначальний лінійний розмір для горизонтальних труб – діаметр, вертикальних поверхонь – висота.

в). Горизонтальна пластина: розрахункове значення Nu збільшується на 30%, якщо нагріта поверхня зорієнтована вверх і на 30% зменшується, якщо нагріта поверхня зорієнтована вниз. Визначальний розмір – менша сторона пластини. Для повітря Pr_с/Pr_ст = 1 і наведені формули спрощуються.

В обмеженому просторі (рис.8.2. б) середня густина теплового потоку розраховується за формулами теплопровідності із заміною коефіцієнта теплопровідності середовища еквівалентним . Якщо , приймається . В області приймається .

Визначальний розмір – ширина каналу, визначальна температура – середня температура середовища. Густина теплового потоку: .

П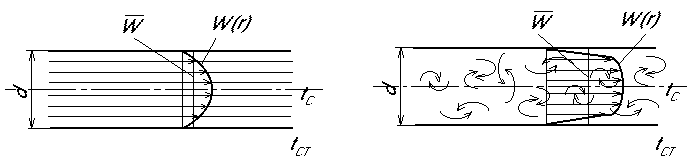 римусова конвекція. Режим течії (рис.5.5) визначається по величині Re.

а) б)

Рис.5.5. Схеми ламінарної (а) і турбулентної (б) течії рідини в трубах.

а). Течія рідини в гладких трубах круглого перетину.

1). ламінарна течія (рис. 3.а) – Re < 2100

Nu= 0,15·Re^0,33·Pr^0,33·(Gr·Pr)^0,1·(Pr_с/Pr_ст)^0,25·ε_l (5.35)

або 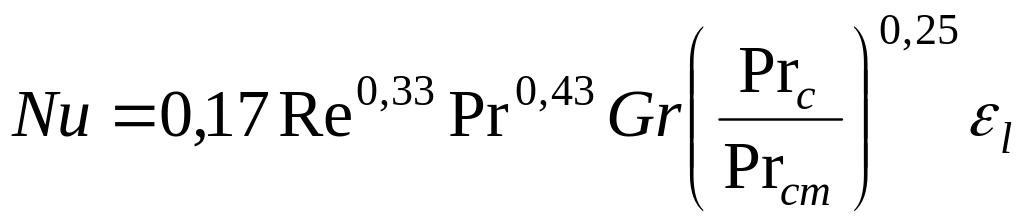, (5.36)

де ε_l - коефіцієнт, що враховує зміну середнього коефіцієнта тепловіддачі по довжині труби і залежить від відношення довжини труби до його діаметра (l/d). Значення цього коефіцієнта представлені в таблиці 5.1.

Таблиця 5.1.

Значення ε_l при ламінарному режимі.

l/d	1	2	5	10	15	20	30	40	50
εl	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1,0

2). перехідний режим – 2100 < Re < 10⁴

Nu= К₀·Pr^0,43·(Pr_с/Pr_ст)^0,25·ε_l . (5.37)

Коефіцієнт К₀ залежить від критерію Рейнольдса Re і представлена в таблиці 5.2.

Таблиця 5.2.

Значення К₀ .

Re?104	2,1	2,2	2,3	2,4	2,5	3	4	5	6	8	10
ДО0	1,9	2,2	3,3	3,8	4,4	6,0	10,3	15,5	19,5	27,0	33,3

3). турбулентна течія (рис.8.3.б) – Re = 10⁴

Nu = 0,021· Re^0,8·Pr^0,43· (Pr_с/Pr_ст)^0,25·ε_l . (5.38)

Значення коефіцієнта ε_l представлені в таблиці 5.3.

Таблиця 5.3.

Значення ε_l при турбулентному режимі.

l/d	εl
	Re = 2·103	Re = 2·104	Re = 2·105
1	1,9	1,51	1,28
2	1,70	1,40	1,22
5	1,44	1,27	1,15
10	1,28	1,18	1,10
15	1,18	1,13	1,08
20	1,13	1,11	1,06
30	1,05	1,05	1,03
40	1,02	1,02	1,02
50	1,00	1,00	1,00

б).Обтікання горизонтальної поверхні. 1). ламінарна течія – Re < 4·10⁴

Nu= 0,66·Re^0,5·Pr^0,33 ·(Pr_с/Pr_ст)^0,25. (5.39)

2). турбулентна течія – Re > 4·10⁴

Nu = 0,037·Re^0,5·Pr^0,33 ·(Pr_с/Pr_ст)^0,25 . (5.40)

Т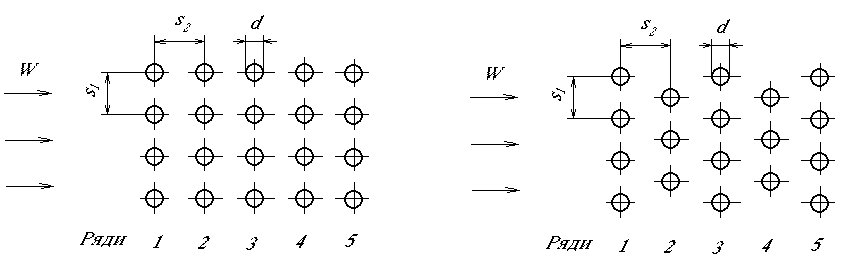 еплообмін при поперечному обтіканні. а). Пучки труб (рис.5.6) (кут атаки  = 90⁰). Використувються два види розташування труб в пучках: коридорне (рис.8.4. а) і шахового (рис.5.6, б).

а) б)

Рис.5.6. Схеми розташування труб в пучках.

Середній коефіцієнт тепловіддачі при може бути визначений з рівняння:

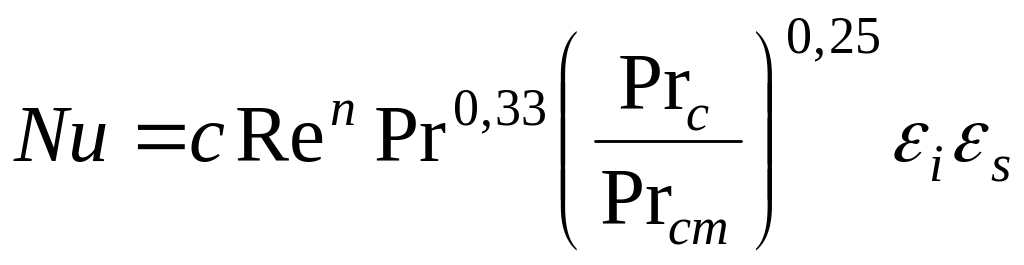. (5.41)

Для шахового пучка ; ; для коридорного ; .

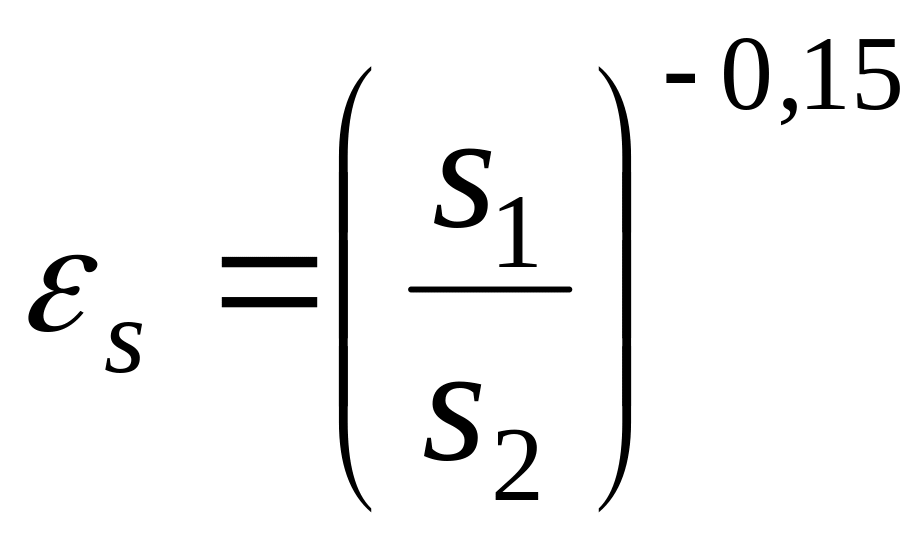Коефіцієнт, який враховує вплив відносних поперечного і поздовжнього кроків для коридорного пучка ; для шахового при ; при .

Коефіцієнт, який враховує номер ряду для першого ряду ; для другого ряду шахового пучка коридорного ; для третього і наступних рядів .

За визначальну температуру приймається середня температура середовища, визначальний розмір – зовнішній діаметр труби, швидкість течії середовища – швидкість в самому вузькому перетині ряду труб.

Середнє значення коефіцієнта тепловіддачі:

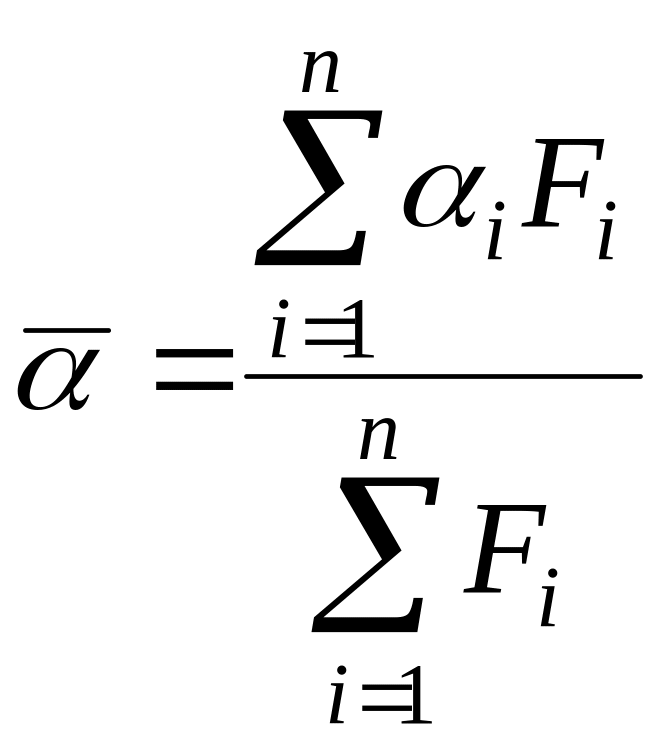, (5.42)

де – середній коефіцієнт тепловіддачі -го ряду; – сумарна площа поверхні труб -го ряду; – число рядів у пучку.

б). Поперечне обтікання одиночної труби. 1). при Re = 5 - 10³

Nu= 0,57·Re^0,5·Pr^0,38 ·(Pr_с/Pr_ст)^0,25 . (5.43)

2). при Re = 10³ - 2·10⁵

Nu = 0,25 Re^0,6·Pr^0,38 ·(Pr_с/Pr_ст)^0,25 . (5.44)

Теплопередача – процес переносу тепла від одного теплоносія (гарячого) до другого (холодного) через стінку, що розділяє їх.

Запишемо вирази для густини теплового потоку при теплопередачі через плоску одношарову стінку (рис.5.7):

конвективна тепловіддача від середовища з більш високою температурою до лівої грані стінки

, (5.45)

передача тепла теплопровідністю через стінку товщиною 

, (5.46)

конвективна тепловіддача від правої грані стінки до другого (холодного) середовища

. (5.47)

При стандартній тепловіддачі усі три теплові потоки повинні бути однаковими і постійними у часі, тобто:

q₁=q₂=q₃=q. (5.48)

З наведених рівнянь знаходимо часткові температурні перепади:

, (5.49)

, (5.48)

. (5.49)

Знаходимо повний температурний перепад процесу теплопередачі складанням часткових перепадів і вирішенням системи рівнянь відносно теплового потоку:

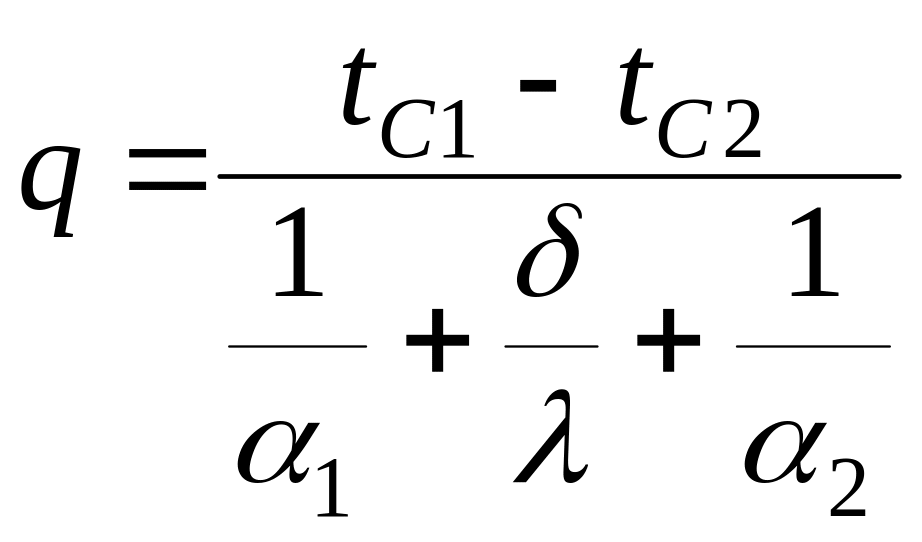. (5.50)

Позначимо 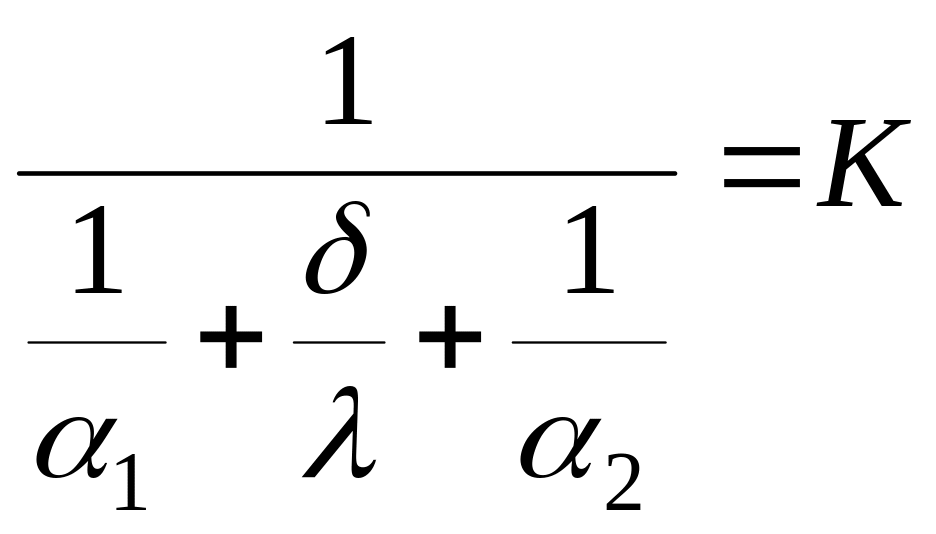і отримаємо рівняння теплопередачі через плоску стінку:

. (5.51)

Коефіцієнт пропорційності К, Вт/м²К, називається коефіцієнтом теплопередачі.

Величина, зворотна коефіцієнту теплопередачі 1/К, називається повним термічним опором теплопередачі ( R_пов).

. (5.52)

Величини , і називаються частковими опорами тепловіддачі (R₁ і R₃ ) і теплопровідності стінки ( R₂ ).

Якщо стінка складається із п шарів то можна записати:

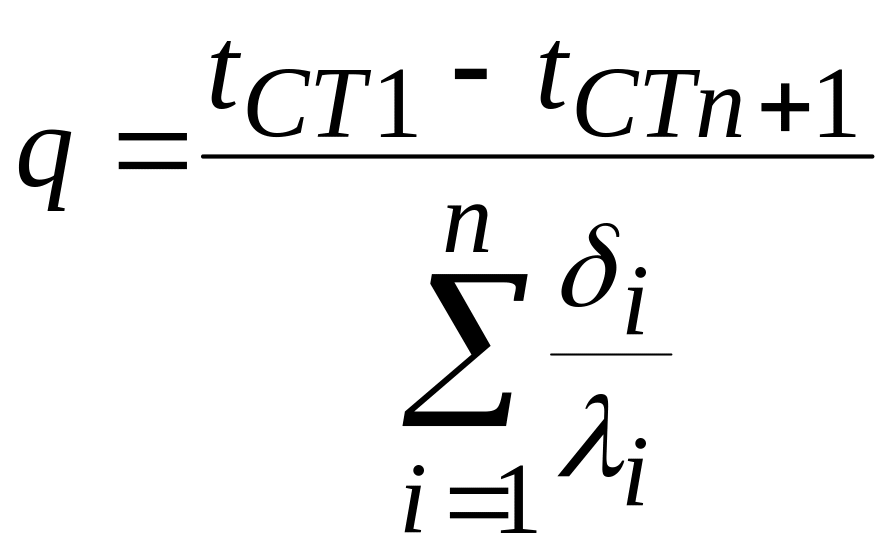, (5.53)

Тоді рівняння теплопередачі через плоску стінку набуде вигляду:

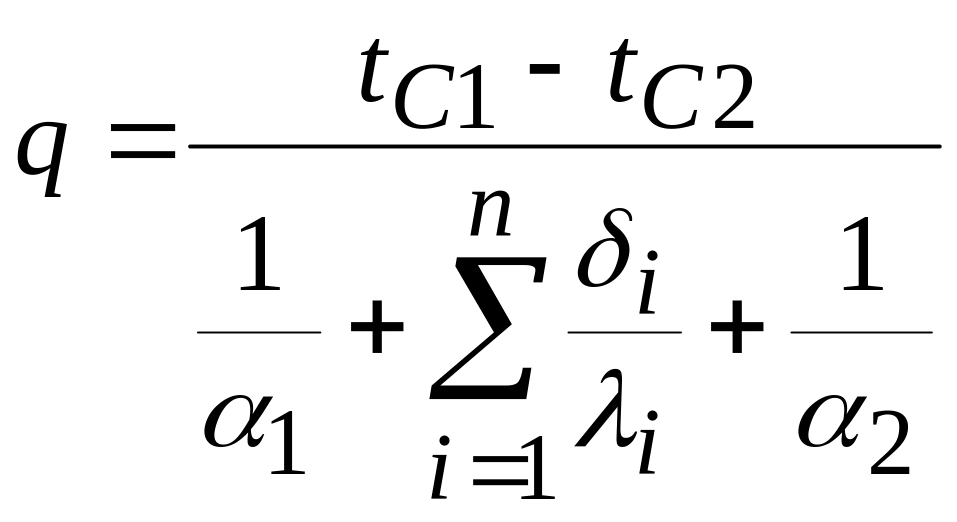. (5.54)

Коефіцієнт теплопередачі через багатошарову плоску стінку становить:

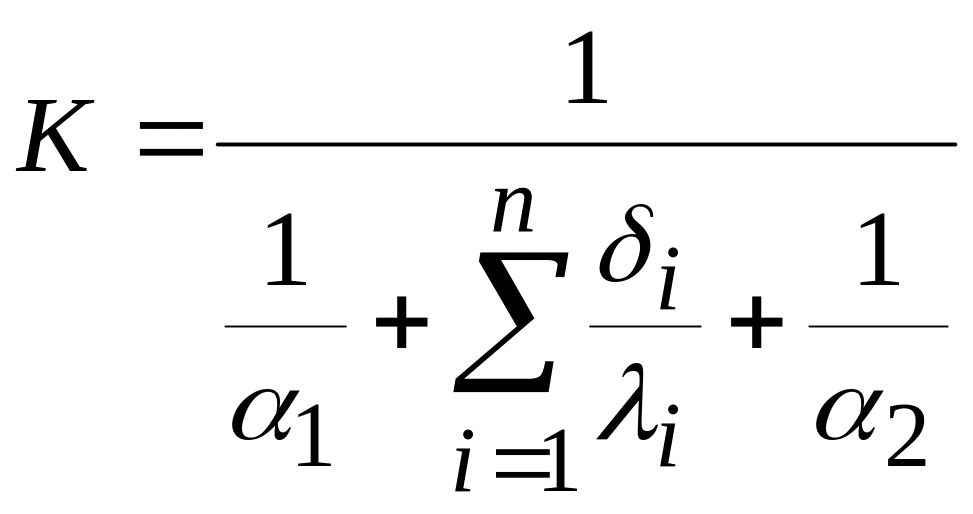. (5.55)

Визначивши кількість тепла, що передається від одного теплоносія до іншого, можна знайти значення температур на поверхнях стінки:

, (5.56)

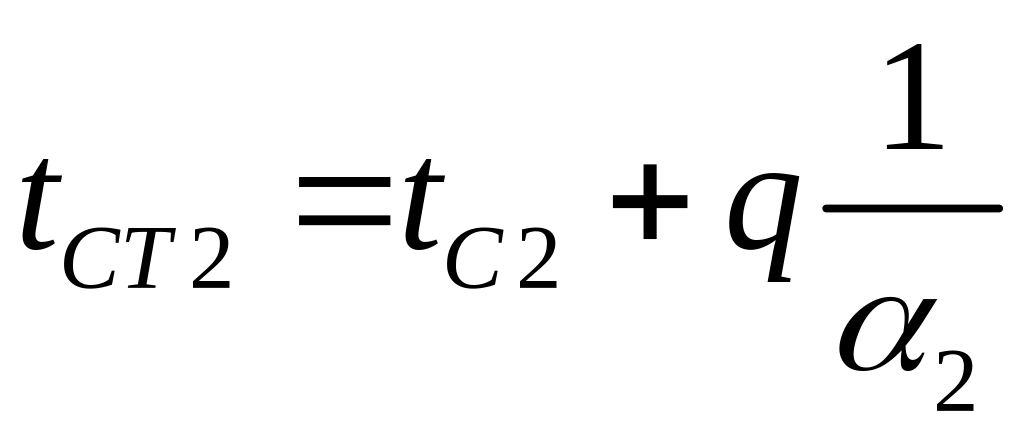. (5.57)