
- •Передмова.
- •1. Основні поняття та закони термодинаміКи
- •Задачі для самостійного вирішення
- •2. Термодинамічні політропні процеси з ідеальними газами
- •З урахуванням виразу :
- •Характеристики політропних процесів
- •Задачі для самостійного вирішення
- •Значення ізобарної, ізохорної теплоємностей та показника адіабати
- •3. Властивості і процеси реальних газів і парів
- •Задачі для самостійного вирішення
- •4. Цикли паросилових і холодильних установок
- •Задачі для самостійного вирішення
- •5. Основи теплообміну
- •Задача для самостійного вирішення
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
ТЕХНОЛОГІЙ ТА ДИЗАЙНУ
ТЕРМОДИНАМІКА І ТЕПЛОПЕРЕДАЧА
Методичні вказівки
до виконання
РОЗРАХУНКОВО-ГРАФІЧНОЇ РОБОТИ
для студентів
усіх спеціальностей і форм навчання
Київ КНУТД 2010
Термодинаміка і теплопередача: Методичні вказівки до виконання розрахунково-графічної роботи длястудентів усіх спеціальностей і форм навчання / Упор.: Б.М.Злотенко, Л.Д.Порхун.- К.: КНУТД, 2010.- 64 с.
Укр. мовою
Упорядники: Б.М. Злотенко, д.т.н., професор
Л.Д. Порхун, доцент
.
Відповідальний за випуск завідувач кафедри тепломасообмінних процесів д.т.н., професор Б.М.Злотенко
Затверджено на засіданні кафедри тепломасообмінних процесів Протокол № 6 від 17.02.2009 р.
Передмова.
Розрахунково-графічна робота з теплотехнічних дисциплін виконується при підготовці студентів за базовими технічними напрямками вищої освіти.
Дисципліни "Термодинаміка і теплопередача", "Термодинаміка і теплотехніка", "Теоретичні основи теплотехніки" вивчаються при підготовці бакалаврів технічних напрямків і засновані на знаннях, отриманих ними при вивченні фундаментальних дисциплін: фізики, хімії, вищої математики.
Розрахунково-графічна робота сприяє розвитку практичних навичок студентів в області розрахунку та проектування теплотехнічних процессів і базується на теоретичних положеннях, вивчених у розглянутих раніше дисциплінах.
При виконанні розрахунково-графічної роботи студент самостійно вирішує задачі, виконує необхідні графічні побудови діаграм теплових процесів і схем теплотехнічних установок.
У даних методичних вказівках наведені теоретичні відомості з основних розділів теплотехнічних дисциплін, завдання для самостійного розв’язання задач, а також приклади виконання основних розрахунків і графічних побудов, що визначають зміст розрахунково-графічної роботи.
Розрахунково-графічна робота оформляється на аркушах формату А4 з титульною сторінкою, на якій вказуються група і прізвище студента.
1. Основні поняття та закони термодинаміКи
Поступова зміна стану тіла, що відбувається в результаті його взаємодії з навколишнім середовищем, називається термодинамічним процесом.
Рівноважні
стани (![]() )
і рівноважний процес (
)
і рівноважний процес (![]() )
можна зобразити у вигляді діаграм (рис.
1.1, а).
)
можна зобразити у вигляді діаграм (рис.
1.1, а).
Круговим процесом або циклом називається процес, в результаті здійснення якого тіло повертається у початковий стан (рис. 1.1, б).
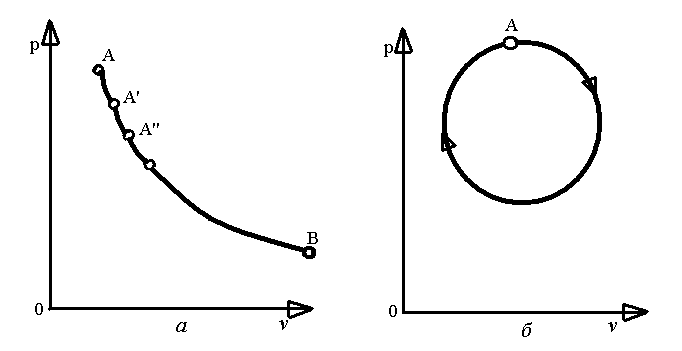
Рис.1.1. Діаграми термодинамічних процесів.
Т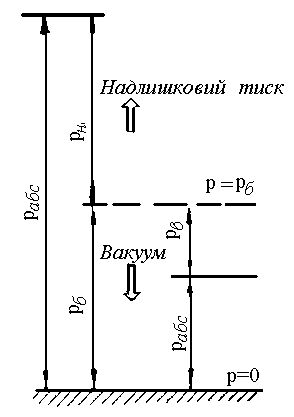 ермічні
параметри стану.
Якщо тиск робочого тіла більший за
атмосферний, тоді використовують
манометр,
який
фіксує надлишковий тиск
ермічні
параметри стану.
Якщо тиск робочого тіла більший за
атмосферний, тоді використовують
манометр,
який
фіксує надлишковий тиск
![]() (рис. 1.2).
(рис. 1.2).
Рис. 1.1. Схема до розрахунку абсолютного тиску.
![]() (1.1)
(1.1)
Якщо
тиск в посудині менший за барометричний,
тоді застосовують прилад – вакуумметр,
який фіксує розрідження, або вакууметричний
тиск
![]() ,
тобто показує, наскільки тиск в посудині
менший за атмосферний
,
тобто показує, наскільки тиск в посудині
менший за атмосферний
![]() .
(1.2)
.
(1.2)
![]() (1.3)
(1.3)
Абсолютна температура вимірюється за шкалою Кельвіна:
![]() .
(1.4)
.
(1.4)
де
![]() – температура за шкалою Цельсія.
– температура за шкалою Цельсія.
Питомий
об’єм,
![]() ,
м3/кг
– об’єм, що займає одиниця маси речовини:
,
м3/кг
– об’єм, що займає одиниця маси речовини:
![]() ,
(1.5),
,
(1.5),
де
![]() – маса речовини, кг;
– маса речовини, кг;
![]() – об’єм, який вона займає, м3.
– об’єм, який вона займає, м3.
Термодинамічне рівняння стану. Для 1 кіломоля ідеального газу рівняння стану має вигляд рівняння Клапейрона-Менделєєва:
![]() ,
(1.6)
,
(1.6)
де
![]() – абсолютний тиск, Па;
– абсолютний тиск, Па;
![]() – об’єм 1 кіломоля газу,
– об’єм 1 кіломоля газу,
![]() ;
;
![]() – універсальна газова стала;
– універсальна газова стала;
![]() – абсолютна температура, К.
– абсолютна температура, К.
Значення
![]() розраховується для нормальних умов:
розраховується для нормальних умов:
![]() .
(1.6):
.
(1.6):
![]() .
(1.7)
.
(1.7)
Для 1 кг ідеального газу:
![]() ,
(1.8)
,
(1.8)
де
![]() – питомий об’єм газу;
– питомий об’єм газу;
![]() – питома газова стала,
– питома газова стала,
![]() ;
;
![]() – маса 1 кіломоля,
– маса 1 кіломоля,
![]() .
.
Помноживши (1.8) на масу газу, одержимо рівняння стану для довільної кількості речовини:
![]() .
(1.9)
.
(1.9)
де
![]() – об’єм маси газу,
– об’єм маси газу,
![]() .
.
Для проведення термодинамічних розрахунків систем з газовими сумішами чи розчинами необхідно знайти їхній склад. Склад суміші може бути заданий:
масовими частками
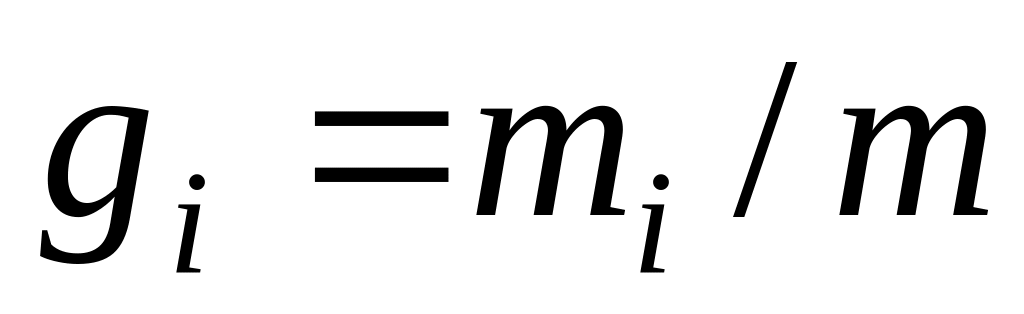 ,
де
,
де
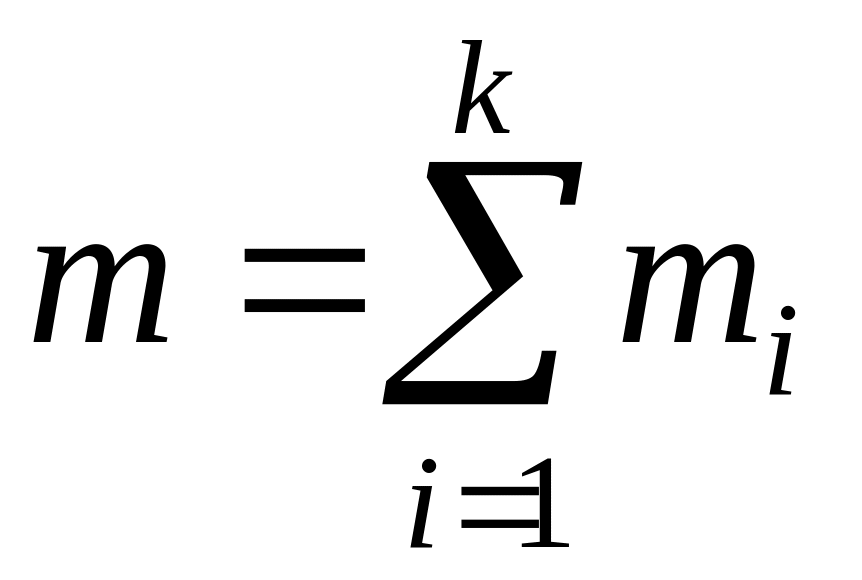 ;
;
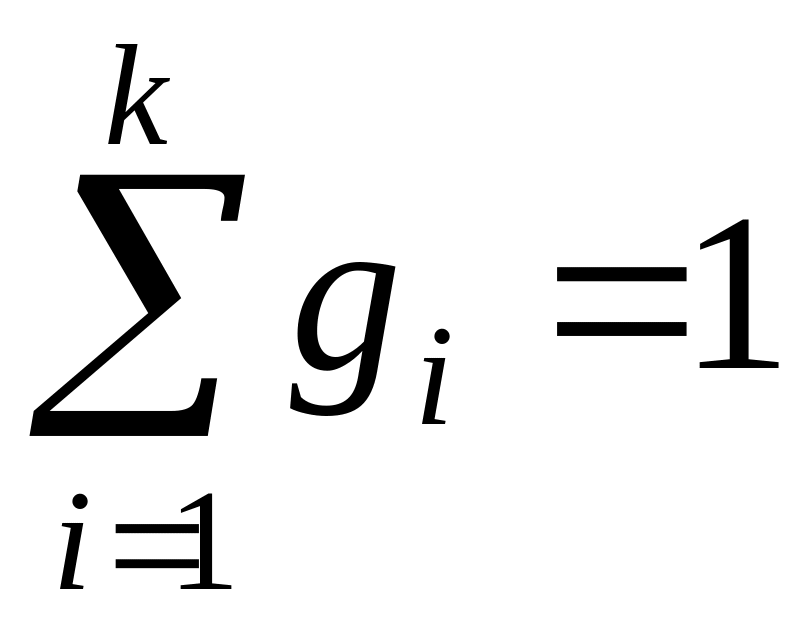 ;
;
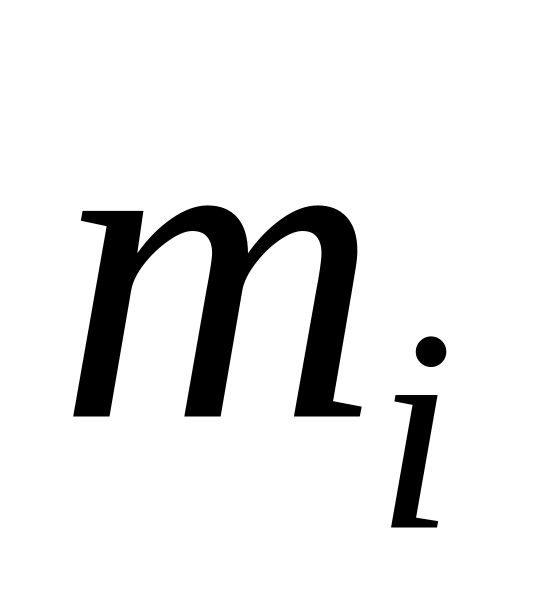 і
– маси компонента і суміші;
і
– маси компонента і суміші;мольними частками
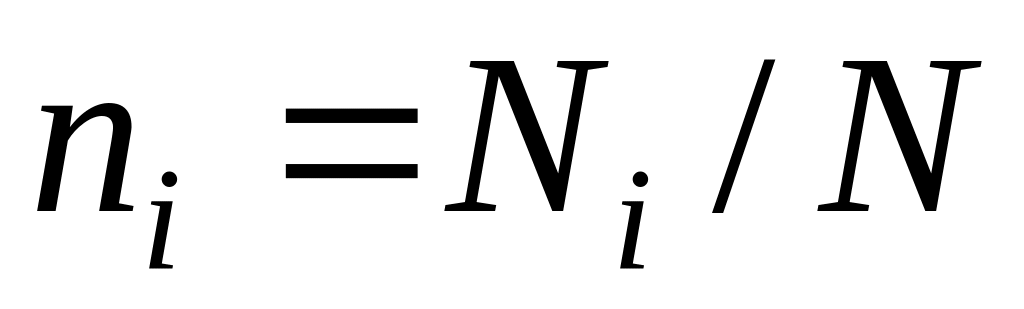 ,
де
,
де
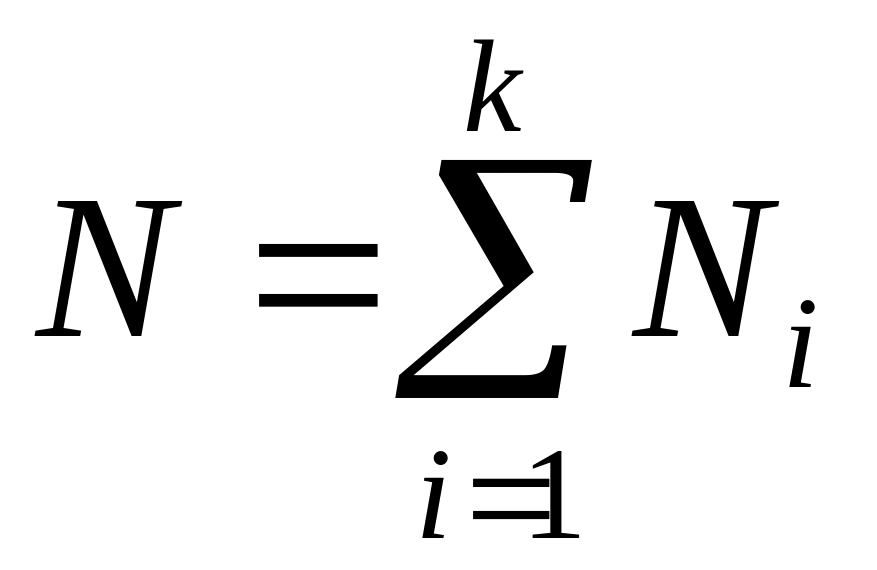 ;
;
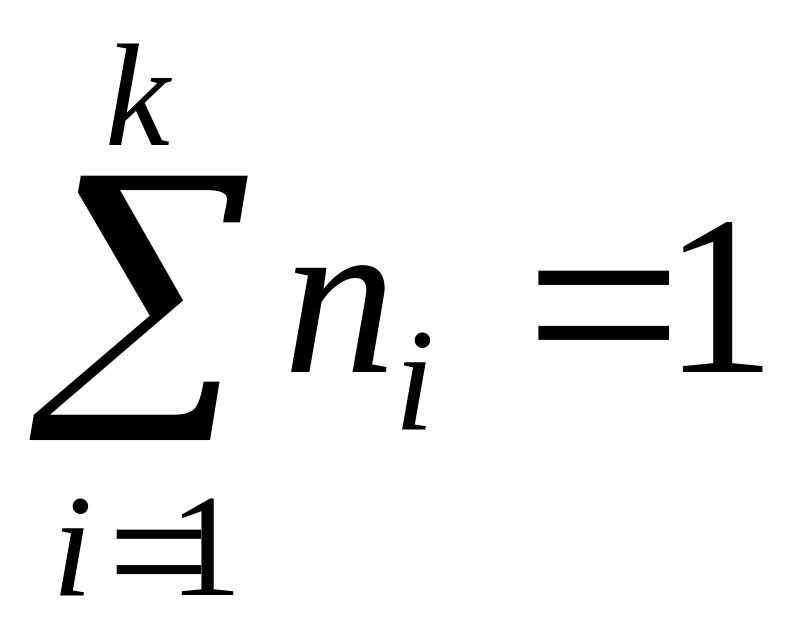 ;
;
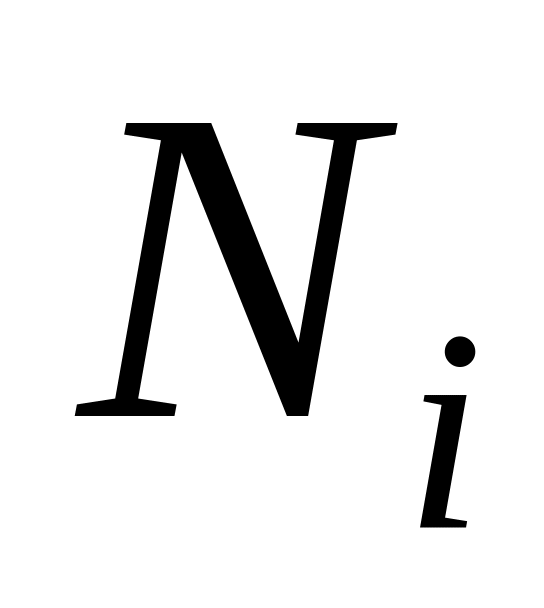 і
і
 – число кіломолів компонента і суміші;
– число кіломолів компонента і суміші;об'ємними частками
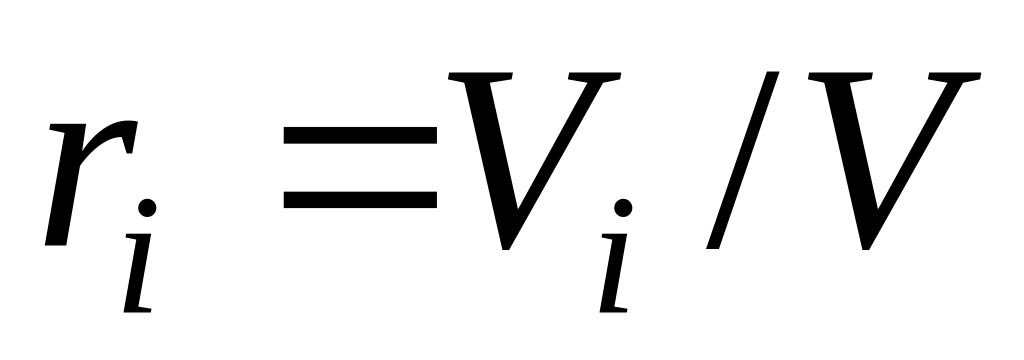 ,
де
,
де
 (закон Амага);
(закон Амага);
 ;
;
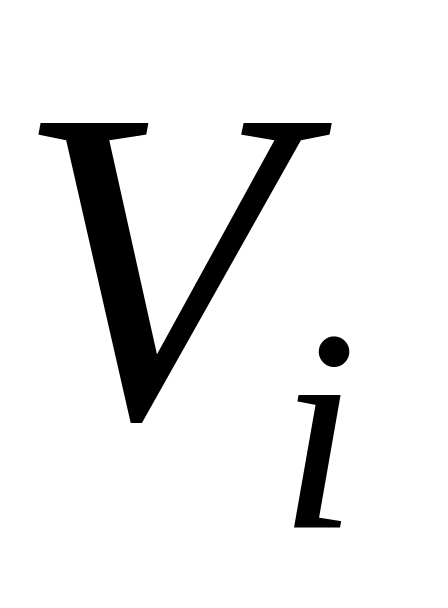 і
– об'єми компонента (приведений об'єм)
і суміші при однакових тиску і температурі;
і
– об'єми компонента (приведений об'єм)
і суміші при однакових тиску і температурі;
Оскільки
згідно закону Авагадро мольні об'єми
всіх компонентів суміші газів рівні,
то
![]() ,
а
,
а
![]() .
Тоді
.
Тоді
![]() .
.
Склад суміші ідеальних газів може бути також заданий парціальними тисками рi. Парціальний тиск рi – це тиск i-го компонента газової суміші за умови, що він займає весь об'єм, призначений для суміші, при температурі суміші.
Закон Дальтона. Сума парціальних тисків окремих газів, що входять у суміш, дорівнює повному тиску суміші тобто:
![]() .
(1.10)
.
(1.10)
Таким чином, кожен газ у посудині займає весь об'єм при температурі суміші, знаходячись під власним парціальним тиском.
Рівняння стану для i-го компонента газової суміші:
![]() .
(1.11)
.
(1.11)
Рівняння стану для суміші ідеальних газів має вигляд:
![]() .
(1.12)
.
(1.12)
![]() –
газова
стала суміші
;
–
газова
стала суміші
;
![]() – маса 1 кіломоля суміші,
.
– маса 1 кіломоля суміші,
.
 .
(1.13)
.
(1.13)
Калоричні
параметри стану .
Внутрішня енергія
![]() ,
Дж, – це
енергія,
яка складається з кінетичної енергії
хаотичного руху молекул і потенціальної
енергії взаємодії молекул. Питома
внутрішня енергія вимірюється в Дж/кг:
,
Дж, – це
енергія,
яка складається з кінетичної енергії
хаотичного руху молекул і потенціальної
енергії взаємодії молекул. Питома
внутрішня енергія вимірюється в Дж/кг:
![]() .
(1.14)
.
(1.14)
Зміна внутрішньої енергії в будь-якому процесі:
![]() (1.15)
(1.15)
Для замкненого (кругового) процесу зміна внутрішньої енергії:
![]() .
(1.16)
.
(1.16)
Енергія
газу, що знаходиться у зовнішньому
середовищі з тиском
і займає об’єм
,
складається з внутрішньої енергії
![]() і потенціальної енергії тиску
і потенціальної енергії тиску
![]() і називається ентальпією газу в даному
стані:
і називається ентальпією газу в даному
стані:
![]() .
(1.17)
.
(1.17)
Розглянемо повну енергію газу під поршнем з вантажем G (рис. 1.3).
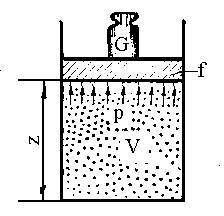
Рис. 1.3. Схема до визначення ентальпії.
Ентальпія газу в посудині під поршнем:
![]() .
(1.18)
.
(1.18)
Потенціальна енергія тиску:
![]() .
(1.19)
.
(1.19)
Зміна ентальпії не залежить від характеру процесу, а залежить лише від початкового і кінцевого станів:
![]() .
(1.20)
.
(1.20)
Ентропія – параметр стану, диференціал якого дорівнює відношенню нескінченно малої кількості тепла в елементарному оборотному процесі до абсолютної температури, яка на малій ділянці процесу є постійною величиною:
![]() ;
;
![]() .
(1.21)
.
(1.21)
Зміна ентропії в будь-якому процесі:
![]() .
(1.22)
.
(1.22)
Всі ці параметри мають властивість адитивності.
Термодинамічний
процес і його енергетичні характеристики.
Енергетичними характеристиками
термодинамічного процесу є робота (![]() )
і теплота
)
і теплота
![]() .
.
Елементарна питома робота проти зовнішніх сил:
![]() .
(1.23)
.
(1.23)
Для кінцевого процесу (рис.1.4):
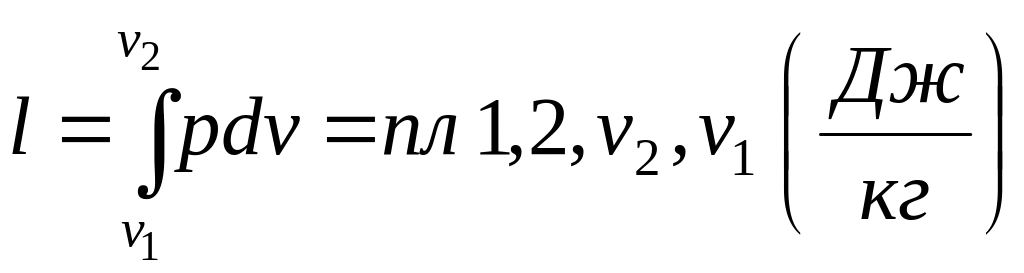
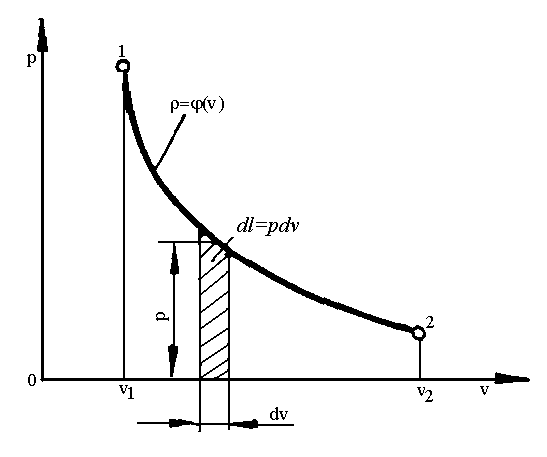 .
(1.24)
.
(1.24)
Рис. 1.4. Схема до обчислення роботи в термодинамічному процесі.
Елементарна питома теплота:
![]() .
(1.25)
.
(1.25)
Для кінцевого процесу кількість тепла, віднесеного до 1 кг речовини (рис.1.5):
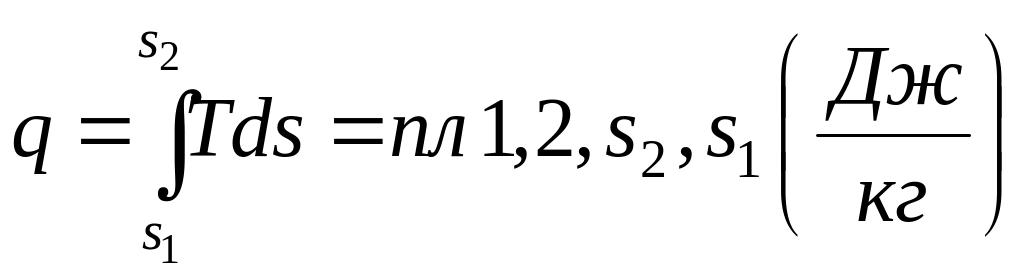
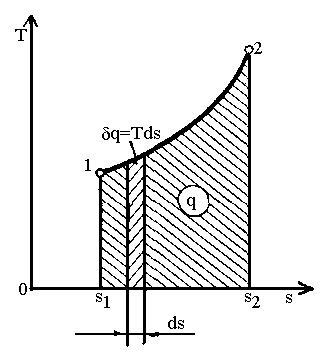 .
(1.26)
.
(1.26)
Рис.
1.5.
![]() діаграма термодинамічного процесу.
діаграма термодинамічного процесу.
Теплоємність – відношення теплоти, яка підводиться або відводиться у процесі до відповідної зміни температури тіла:
![]() .
Істинна теплоємність:
.
Істинна теплоємність:
![]() .
(1.27)
.
(1.27)
Розрізняють
теплоємності: масову
![]() ,
кДж/(кгК),
віднесену до 1 кг робочого тіла; об’ємну
,
кДж/(кгК),
віднесену до 1 кг робочого тіла; об’ємну
![]() ,
кДж/(м3К),
віднесену до 1 м3
при нормальних умовах;
,
кДж/(м3К),
віднесену до 1 м3
при нормальних умовах;
![]() ,
кДж/(кмольК),
віднесену до 1 кмоля речовини. Зв’язок
між цими теплоємностями такий:
,
кДж/(кмольК),
віднесену до 1 кмоля речовини. Зв’язок
між цими теплоємностями такий:
![]() ;
;
![]() .
(1.28)
.
(1.28)
Для ідеальних газів зв’язок між ізобарною і ізохорною теплоємностями встановлює закон Майєра:
![]() .
(1.29)
.
(1.29)
Для мольних теплоємностей:
![]() кДж/(кмольК).
(1.30)
кДж/(кмольК).
(1.30)
Відношення ізобарної і ізохорної теплоємностей називається показником адіабати:
![]() .
(1.31)
.
(1.31)
Теплоємність залежить від температури (рис.1.6):
![]() (1.32)
(1.32)
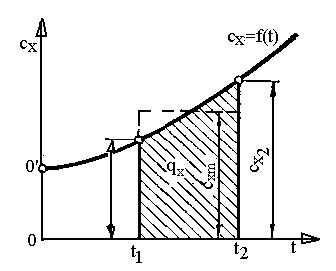
Рис.1.6. Залежність теплоємності від температури.
Для практичних розрахунків приймають:
![]() .
(1.33)
.
(1.33)
Виходячи з поняття істинної теплоємності, кількість питомої теплоти в процесі:
 .
(1.34)
.
(1.34)
Ця ж кількість питомої теплоти, виражена через середню теплоємність:
![]() .
(1.35)
.
(1.35)
Тоді середня теплоємність
![]()
 .
(1.36)
.
(1.36)
Здійснимо перетворення
 .
(1.37)
.
(1.37)
Проте
 ;
;
 .
(1.38)
.
(1.38)
Тоді остаточно
![]() .
(1.39)
.
(1.39)
Кількість теплоти в процесі для маси m, кг, чи об’єму V, м3, речовини:
![]() .
(1.40)
.
(1.40)
Теплоємність газової суміші:
масова
![]() ;
об’ємна
;
об’ємна
![]() ;
мольна
;
мольна
![]() .
(1.41)
.
(1.41)
Перший закон термодинаміки. В термодинамічному процесі кількість теплоти Q, яка підведена до системи, витрачається на зміну внутрішньої енергії U і на виконання зовнішньої роботи L:
Q=U + L. (1.42)
Для 1 кг речовини:
![]() .
(1.43)
.
(1.43)
![]() .
(1.44)
.
(1.44)
Рівняння першого закону термодинаміки можна представити у вигляді схеми енергобалансу в термодинамічному процесі (рис.1.7).
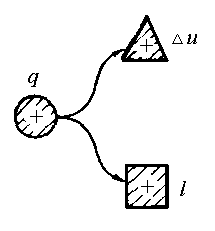
Рис.1.7. Схема енергобалансу в термодинамічному процесі.
Для кругового процесу 1-й закон:
![]() .
(1.45)
.
(1.45)
Перша форма запису 1-го закону:
![]() або
або
![]() . (1.46)
. (1.46)
Проведемо перетворення:
![]() ;
(1.47)
;
(1.47)
![]() ;
(1.48)
;
(1.48)
![]() .
(1.49)
.
(1.49)
Підставивши
значення
![]() у рівняння першої форми, отримаємо другу
форму запису 1-го закону:
у рівняння першої форми, отримаємо другу
форму запису 1-го закону:
![]() або
або
![]() . (1.50)
. (1.50)
Якщо
об’єднати першу, другу форми запису і
рівняння
![]() ,
знайдемо основне рівняння термодинаміки
або термодинамічну тотожність:
,
знайдемо основне рівняння термодинаміки
або термодинамічну тотожність:
![]() .
(1.51)
.
(1.51)
Для необоротних процесів:
![]() або
або
![]() .
(1.52)
.
(1.52)
