2.2.1. Характеристика модели «объем – издержки - прибыль»

Модель «объем – издержки – прибыль» отражает поведение важнейших параметров деятельности предприятия – издержек, выручки от реализации и прибыли - под воздействием такого фактора как объем деятельности. Геометрическая интерпретация данной модели представлена на рисунке 2.2.

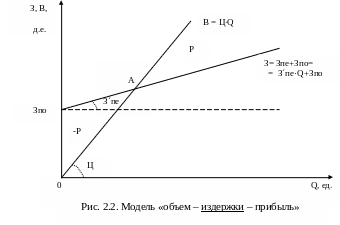
В данном случае для описания поведения издержек используется

линейная зависимость, формула (2.1):

З(Q) = З´пе ·Q + Зпо, (2.1)

где

Q – объем деятельности в рассматриваемом периоде, ед.,

З(Q) – полные издержки при объеме деятельности Q, д.е.,

З´пе – удельные переменные издержки, д.е.,

Зпо – постоянные издержки, д.е.

Как известно, переменными называются издержки, общая сумма которых (валовые издержки) изменяется пропорционально изменению объема деятельности. Удельные переменные издержки при изменении объема деятельности как раз не изменяются, то есть остаются постоянными.

Постоянные же издержки, наоборот, в общей массе (валовые) остаются неизменными при изменении объемов деятельности в рассматриваемом периоде, а удельные постоянные издержки при увеличении объема деятельности уменьшаются.

Геометрически величина постоянных издержек равна длине отрезка

от начала координат до начала линии издержек, которую обычно называют

линией сметы. Удельные переменные издержки, что легко доказать, это

тангенс угла наклона линии издержек относительно горизонтальной оси.

Выручка от реализации продукции (В) представляет собой произведение:

В(Q) = Ц ∙ Q, (2.2)

где

Ц – цена реализации, д.е.,

В(Q) – выручка от реализации Q единиц продукции, д.е.

Геометрически линия выручки берет начало в точке начала координат, цена при этом представляет собой тангенс угла наклона этой линии по отношению к горизонтальной оси.

Как известно, прибыль (Р) представляет собой разность:

Р(Q) = В(Q) – З(Q). (2.3)

Геометрически прибыль на данном графике представляет собой область, заключенную между линией выручки и линией сметы, расположенную правее точки А (точка пересечения линии выручки и линии сметы). Соответствующая область, расположенная левее точки А, представляет собой область убытка.

Модель “объем - издержки – прибыль” (модель «ОИП»), получившая в ХХ-ом веке широкое распространение, представляет собой теоретическую основу для обоснования большого числа управленческих решений. Основным фактором риска операционной деятельности предприятия является наличие постоянных издержек. Данная модель позволяет определить ряд полезных характеристик деятельности предприятия, позволяющих учитывать и контролировать данное обстоятельство. К числу таких характеристик в первую очередь относится показатель маржинального дохода (вклада на покрытие), который представляет собой разность между выручкой от реализации и валовыми переменными издержками при определенном объеме деятельности:

МД(Q) = В(Q) – Зпе(Q), (2.4)

Помимо рассчитанного по формуле (2.4) совокупного (валового) маржинального дохода может быть определен также и удельный маржинальный доход (МД')

МД' = Ц - З'пе, (2.4.а)

Понятно, что показатель совокупного маржинального дохода зависит от объема деятельности. А удельный маржинальный доход в случае линейного поведения функций издержек и выручки является величиной, не зависящей от объема деятельности, что является очевидным преимуществом данного показателя по сравнению с показателем удельной прибыли.

Связь между валовым и удельным маржинальным доходом очевидна:

МД(К) = В(К) – Зпе(К) = Ц · К - З'пе · К =

= (Ц - З'пе) · К = МД' · К.

Легко доказать, что маржинальный доход представляет собой сумму постоянных издержек и прибыли:

МД(Q) = Зпо + Р(К).

Геометрическая интерпретация маржинального дохода представлена на рисунке 2.3. Понятно, что предприятие будет получать прибыль только после того как сможет покрыть выручкой не только переменные, но и постоянные издержки.

На рисунке 2.3 при объеме деятельности Q1 длина отрезка Q1В1 равна соответствующей величине выручки, длина отрезка З0З1 – соответствующей величине валовых переменных издержек, таким образом, суммарная длина отрезков Q1З0 (постоянные издержки) и З1В1 (прибыль) равна валовому маржинальному доходу при данном объеме деятельности.

Другим, из числа наиболее важных показателей, определяемых на основе модели «ОИП», является точка безубыточности (мертвая точка, порог рентабельности), то есть такое количество единиц реализованной продукции, при котором валовые издержки равны соответствующей выручке. Это означает, что при таком объеме деятельности нет прибыли, но нет и убытка. На графике 2.2 точка безубыточности обозначена Q* (основание перпендикуляра, опущенного из точки А на горизонтальную ось).

Аналитически формула для расчета величины точки безубыточности определяется из условия:

В(Q*) = P(Q*),

что означает пересечение линий выручки и сметы (точка А). Как известно, формула для нахождения точки безубыточности выглядит следующим образом:

Q* = Зпо / (Ц - З´пе) = Зпо / МД´, (2.5)

где

Q* - точка безубыточности, ед.

Помимо точки безубыточности в расчетах часто используется показатель безубыточного оборота (В*), а именно, значение выручки от реализации, которую получает предприятие в точке безубыточности. Очевидно, что величина безубыточного оборота равна величине соответствующих полных валовых издержек. На рисунке 2.3. безубыточный оборот обозначен символом В* (основание перпендикуляра , опущенного из точки А на вертикальную ось).

Для расчета величины безубыточного оборота используется показатель уровня маржинального дохода (Нмд):

Нмд = МД(Q) / В(Q) = МД´ / Ц. (2.6)

Экономический смысл данного показателя может быть выражен следующим образом: уровень маржинального дохода отражает долю маржинального дохода в каждой денежной единице, полученной от реализации продукции.

Легко доказать, что величина безубыточного оборота рассчитывается следующим образом:

В* = Зпо / Нмд. (2.7)

Показатель безубыточного оборот продукции, как правило используется в тех случаях когда предприятие производит и продает несколько видов продукции.

На основе показателей точки безубыточности и безубыточного оборота могут быть определены показатели, которые используются для характеристики безопасности операционной деятельности. К их числу, прежде всего, относится так называемый показатель зоны операционной безопасности, характеризующий “отдаленность” рассматриваемого объема деятельности от точки безубыточности, то есть от положения риска, после которого предприятие попадает в зону убытка:

Zоб = Q1 - Q*, (2.8)

где

Zоб – зона операционной безопасности, ед.,

Q1 – рассматриваемый объем деятельности, ед.,

Q* - точка безубыточности, ед.

Данный показатель является величиной абсолютной, что делает его использование не всегда удобным. В связи с этим более интересным является показатель уровня операционной безопасности:

Уоб = Zоб / Q1 = (Q1 - Q*) / Q1. (2.9)

Очевидно, аналогичные характеристики могут быть рассчитаны и на основе показателя безубыточного оборота.

Модель «ОИП» построена на ряде сильных допущений, к числу которых относятся следующие моменты:

1. Функция выручки линейна,

2. Строгое разделение затрат на переменную и постоянную составляющие,

функция затрат линейна,

3. Существование единственной точки безубыточности,

4. Равенство между объемами производства и реализации,

5. Постоянный ассортимент.

Рассмотренная постановка модели «объем – издержки - прибыль» используется в детерминированных ситуациях. В ситуациях риска или неопределенности могут быть использованы ее соответствующие модификации ( см., например, [2], [4]).