
- •Ставрополь, 2013 г. Фгаоу впо «Северо-Кавказский федеральный университет»
- •Задание
- •1 Анализ использования задач суммирования чисел по модулю в криптографических приложениях 11
- •2 Аналитический обзор архитектуры и принципов построения современных цифровых сигнальных процессоров 14
- •3 Разработка практических рекомендаций по использованию алгоритмов суммирования чисел по модулю для цифрового сигнального процессора 23
- •Список используемых сокращений
- •Введение
- •Анализ использования задач суммирования чисел по модулю в криптографических приложениях
- •1Обзор проблем защиты информации в компьютерных системах
- •2Обзор основных задач криптографии использующих суммирование чисел по модулю
- •Задача обеспечения секретности передаваемых сообщений
- •Использование криптографических методов при автоматизации процессов передачи и обработки информации
- •3Выводы по главе
- •Аналитический обзор архитектуры и принципов построения современных цифровых сигнальных процессоров
- •4Классификация универсальных и специализированных цифровых сигнальных процессоров
- •5Общие аппаратные архитектуры используемые для цифровой обработки сигналов
- •5.1Основные особенности гарвардской архитектуры
- •5.2Особенности конвейерной обработки задач
- •5.3Общие принципы построения аппаратных умножителей
- •6Общие принципы построения универсальных цифровых сигнальных процессоров
- •6.1Особенности архитектуры с фиксированной запятой
- •6.2Построение процессоров с плавающей запятой
- •7Особенности построения специализированных цифровых сигнальных процессоров
- •8Выводы по главе
- •Разработка практических рекомендаций по использованию алгоритмов суммирования чисел по модулю для цифрового сигнального процессора
- •9Классификация и основные принципы построения сумматоров
- •10Схемотехнические решения построения сумматоров
- •11Обоснование основных требований к аппаратным средствам реализации алгоритмов суммирования чисел по модулю в криптографических приложениях
- •12Синтез алгебраических основ суммирования чисел по произвольному модулю
- •13Алгоритм нахождения суммы чисел по модулю
- •14Алгоритм реализации многоразрядного параллельного сумматора по модулю с последовательным переносом
- •15Выводы по главе
- •Заключение
- •Список использованных источников
- •Приложение а
Разработка практических рекомендаций по использованию алгоритмов суммирования чисел по модулю для цифрового сигнального процессора
9Классификация и основные принципы построения сумматоров
Основной элементарной операцией, выполняемой над кодами чисел в цифровых устройствах, является арифметическое сложение.
10Схемотехнические решения построения сумматоров
Построение двоичных сумматоров обычно начинается с сумматора по модулю 2. На рисунке 3.1 приведена таблица истинности этого сумматора.
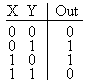
Рисунок 3 - Таблица истинности сумматора по модулю 2
11Обоснование основных требований к аппаратным средствам реализации алгоритмов суммирования чисел по модулю в криптографических приложениях
Как уже было показано выше, для построения цифровых сигнальных процессоров в криптографических приложениях необходимо синтезировать высокопроизводительные арифметические вычислители элементарных групповых операций в конечных полях. К числу таких операций в первую очередь принадлежит операция суммирования чисел по модулю. Настоятельность этой операции заключается в том, что, так как при выполнении суммирования в конечных полях, результаты вычислений формируются вне диапазона значений конечного поля, то необходимо приведение таких значений в область определений заданного конечного поля.
12Синтез алгебраических основ суммирования чисел по произвольному модулю
Основу теоретических исследований составляют следующие утверждения.
Пусть А - любое целое число, представленное в виде:
А = akmk + ak-1mk-1 + ... + a1 m + a0, (3.1)
где
m
- основание, k
+ 1 - разрядность числа А,
а аi
,
i
=
![]() -
коэффициенты числа A
при его представлении в заданной системе
счисления.
-
коэффициенты числа A
при его представлении в заданной системе
счисления.
Пусть B - любое целое число, представленное в виде:
B = bkmk + bk-1mk-1 + ... + b1 m + b0, (3.2)
где
bi
,
i
=
![]() -
коэффициенты числа B
при
его представлении в заданной системе
счисления.
-
коэффициенты числа B
при
его представлении в заданной системе
счисления.
Тогда сумма чисел А и B по модулю Р равна сумме сумма чисел А и B минус значение кода модуля, если сумма превышает значение модуля, нулю, если сумма равна значению модуля и самой сумме этих чисел, если она меньше значения модуля.
13Алгоритм нахождения суммы чисел по модулю
Сущность
предлагаемого алгоритма заключается
в реализации следующего способа
суммирования двух чисел
![]() и
и
![]() по модулю m.
Если (a+b)<m,
то выполняется обычное суммирование
S=a+b
и эта сумма S
является результатом. Если же (S=a+b)>m
и по исходному условию сумма S
при
и
не может превышать 2m-2,
то из суммы S
вычитается значение m
и результат является суммой (a+b)
mod
m.
При этом на выходе переноса сумматора,
осуществляющего вычитание, появляется
сигнал. Данный сигнал является признаком
превышения суммы S
значения m
и используется для выбора результата
(a+b)
или (a+b)-m.
В соответствии с этим полный одноразрядный
сумматор по модулю, из которого затем
может быть составлен сумматор по модулю
для произвольного числа разрядов,
должен выполнить суммирование ai
и bi
разрядов с учетом разряда переноса
pIni
из младших разрядов и полученную сумму
Si
выдать на выход устройства при отсутствии
сигнала переноса модуля со старшего
разряда или вычесть из нее разряд модуля
mi
при наличии такового.
по модулю m.
Если (a+b)<m,
то выполняется обычное суммирование
S=a+b
и эта сумма S
является результатом. Если же (S=a+b)>m
и по исходному условию сумма S
при
и
не может превышать 2m-2,
то из суммы S
вычитается значение m
и результат является суммой (a+b)
mod
m.
При этом на выходе переноса сумматора,
осуществляющего вычитание, появляется
сигнал. Данный сигнал является признаком
превышения суммы S
значения m
и используется для выбора результата
(a+b)
или (a+b)-m.
В соответствии с этим полный одноразрядный
сумматор по модулю, из которого затем
может быть составлен сумматор по модулю
для произвольного числа разрядов,
должен выполнить суммирование ai
и bi
разрядов с учетом разряда переноса
pIni
из младших разрядов и полученную сумму
Si
выдать на выход устройства при отсутствии
сигнала переноса модуля со старшего
разряда или вычесть из нее разряд модуля
mi
при наличии такового.
На рисунке 4 представлена схема полного одноразрядного сумматора по модулю.
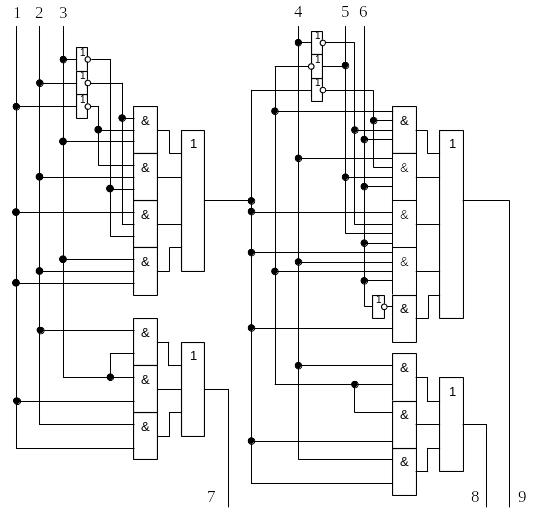
Рисунок 4 - Полный одноразрядный сумматор по модулю
