4.5.Расчет временных параметров сетевого графика

НА СТАДИИ ПЛАНИРОВАНИЯ

Методы расчета. Расчеты графиков производятся вручную или с помощью ЭВМ. Для расчета на ЭВМ временных параметров сетевых графиков разработано значительное количество программ. Вручную, по мнению некоторых авторов, можно рассчитать графики, содержащие до 300 - 400 работ.

В то же время некоторые источники сообщают о ручных расчетах сетевых графиков, состоящих из 7-10 тыс. работ.

Наиболее известны три ручных метода расчета:

а) табличный;

б) матричный;

в) четырехсекторный.

Общим признаком двух первых методов является использование дополнительных специальных форм - таблиц или матриц. Это приводит к необходимости до расчета переносить исходную информацию в специальные расчетные формы и после расчета выходную информацию возвращать обратно на сетевой график. Такой двойной перенос информации, представляет собой неоправданное увеличение затрат и повышает вероятность ошибок за счет дополнительных операций по переносу.

При табличном методе приходится все события комплексного графика после его сшивки заново перенумеровать в порядке натурального ряда чисел без пропусков. Корректировка графика с внесением дополнительных работ и событий приводит к необходимости заново производить перенумерацию.

Матричный метод требует размещения всех работ по двум осям матрицы и этим обусловливает свою непригодность для расчета графиков, содержащих более 100 - 160 работ.

Несмотря на ряд отмеченных недостатков, ручные методы расчета успешно применяются в практике ремонтов.

Табличный метод расчета. Рассмотрим это на примере расчета небольшого абстрактного одноцелевого графика с детерминированными оценками работ при односменном режиме их выполнения (рис.4.7.). В качестве единицы времени принят один день.

После построения графика и выполнения упорядоченной нумерации событий код работ заносится в графу 2 специально подготовленной табличной формы (табл.4.2.). Работы заносятся в возрастающем порядке кода (выписываются все работы, «выходящие» из первого события, затем из второго и т.д.). В графу 1 таблицы проставляется количество предшествующих работ.

Продолжительность работ проставляется в графе 3 на основании исходных данных.

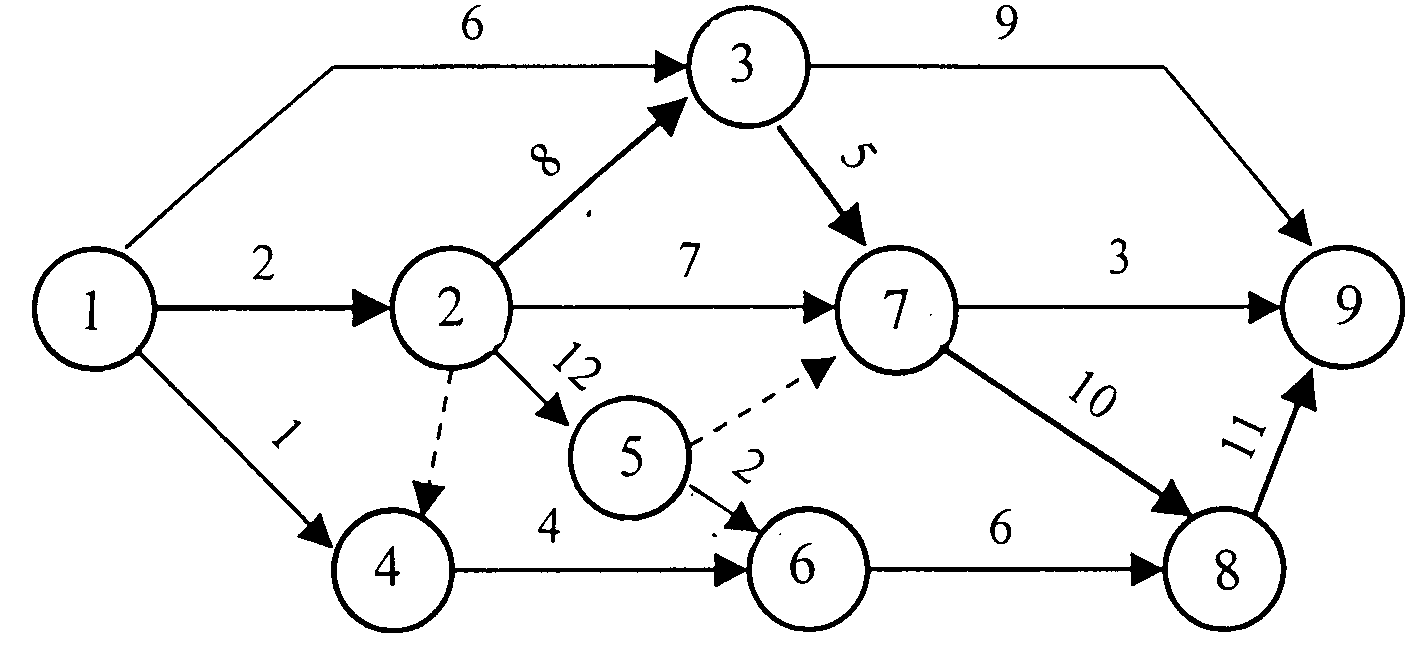
Рис.4.7.Узловой сетевой график из девяти событий.

После заполнения первых трех граф приступают к определению ранних сроков начала и окончания работ. Срок свершения начального события 1 принимается равным нулю. Заносим в первые три строки графы 0.

Ранний срок окончания любой работы равен сумме раннего срока начала её и продолжительности работы. Заносим в первые три строки графы 5 соответственно 2, 6 и 1.

Ранний срок начала последующих работ равен раннему сроку окончания предшествующих работ. Если работе предшествует две или более работ, то срок раннего начала её определяется как максимальная величина ранних сроков окончания предшествующих работ.

Например, для работы 7–9 (рис.4.7.) ранний срок начала работы по пути 1-2-7 равен:

t_рн(7-9) = t_1-2 + t_2-7 = 2 + 7 = 9 дней.

По пути 1-3-7

t_рн(7-9) = t_1-3 + t_3-7 = 6 + 5 = 11 дней.

По пути 1-2-5-7 (с учетом технологической зависимости 5-7)

t_рн(7-9) = t_1-2 + t_2-5 + t_5-7 = 2 + 12 + 0 = 14 дней.

По пути 1-2-3-7

t_рн(7-9) = t_1-2 + t_2-3 + t_3-7 = 2 + 8 + 5 = 15 дней

Таким образом, ранний срок начала работы 7-9 составляет 15 дней.

Ранний срок окончания работы 7-9 равен:

t_ро(7-9) = t_рн(7-9) + t_(7-9) = 15 + 3 = 18 дней.

Ранние сроки начала и окончания работ определяются для всех работ графика последовательно, начиная с начального события.

Максимальная величина из всех ранних сроков окончания работ определяет продолжительность критического пути, в данном случае – 36. Затем определяются работы, лежащие на критическом пути.

Таблица 4.2.Расчет параметров сетевого графика

Количе­ство пред­шеству­ющих работ	Код работы i-j	Продол­житель­ность работы t (i,j)	Раннее начало работы tрн(i,j)	Раннее оконча­ние работы tро(i,j)	Позднее начало работы tпн(i,j)	Позднее оконча­ние работы tпо(i,j)	Полный резерв времени работы Rп(i,j)	Свобод­ный резерв времени работы Rс(i,j)
0	1-2	2	0	2	0	2	0	0
0	1-3	6	0	6	4	10	4	4
0	1-4	1	0	1	14	15	14	1
1	2-3	8	2	10	2	10	0	0
1 1	2-4	0	2	2	15	15	13	0
1	2-5	12	2	14	3	15	1	0
1	2-7	7	2	9	8	15	6	6
2	3-7	5	10	15	10	15	0	0
2	3-9	9	10	19	27	36	17	17
2	4-6	4	2	6	15	19	13	10
1	5-6	2	14	16	22	19	3	0
1	5-7	0	14	14	15	15	1	1
2	6-8	6	16	22	19	25	3	3
3	7-8	10	15	25	15	25	0	0
3	7-9	3	15	18	33	36	18	18
2	8-9	11	25	36	25	36	0	0

Для определения критических работ таблицу просматривают снизу вверх: та работа, у которой максимальный срок раннего окончания (36), лежит на критическом пути (8-9), ранний срок начала её равен сроку раннего окончания предшествующей работы (7-8), лежащей на критическом пути. Как видно из таблицы 4.2.,

t_рн(8-9) = t_ро(7-8); t_рн(7-8) = t_ро(3-7); t_рн(3-7) = t_ро(2-3); t_рн(2-3) = t_ро(1-2).

Критический путь в данном примере определяется работами 1-2, 2-3

3-7, 7-8 и 8-9.

Нахождение поздних сроков начала и окончания работ производится последовательно снизу вверх от конечного до начального события. Поздние сроки окончания работ, заканчивающихся последним событием (9), равны максимальному из сроков ранних окончаний этих работ, т. е. величине критического пути (36). Заносим в последнюю строку графы 7 таблицы величи-ну 36.

Поздний срок начала работы равен разности позднего срока окончания и продолжительности работы, а срок позднего окончания работы равен сроку позднего начала последующей работы. Если у рассматриваемой работы имеются две или более последующих работ, то срок позднего окончания её определяется наименьшей величиной срока позднего начала последующих работ. Поздний срок начала работы можно также определить как разность продолжительности критического пути и самого длинного пути от предшествующего события данной работы до конечного события. Например, для работы 7-9 поздний срок начала работы равен:

t_пн(7-9) = Т_кр – t_(7-9) = 36 – 3 = 33 дня.

Поздний срок окончания работы 7-9:

t_по(7-9) = t_пн(7-9) + t_(7-9) = 33 + 3 = 36 дней.

Для работы 6-8 позднее начало составит:

t_пн(6-8) = Т_кр – (t_(6-8) + t_(8-9)) = 36 – (6 + 11) = 19 дней.

Позднее окончание работы 6-8 наступит через:

t_по(6-8) = t_пн(7-9) + t_(6-8) = 19 + 6 = 25 дней.

Таким образом, заполняются снизу вверх графы 6 и 7 таблицы.

Сопоставление ранних и поздних сроков начала и окончания работ определяет критический путь и резервы времени. Если ранние и поздние сроки начала и ранние и поздние сроки окончания каких-либо работ совпадают, то эти работы лежат на критическом пути и резервы времени у них отсутствуют. Для остальных работ определяются резервы времени, представляющие собой разность поздних и ранних сроков начал и окончаний.

Полный резерв времени определяется разностью позднего и раннего сроков начала или окончания работ. Например, полный резерв времени для работы 7-9 составляет:

R_{п (7-9)} = t_пн(7-9) - t_рн(7-9) = 33 – 15 = 18 дней,

или

R_{п (7-9)} = t_по(7-9) - t_ро(7-9) = 36 – 18 = 18 дней.

Свободный резерв времени определяется как разность между ранним сроком начала последующей работы и ранним сроком окончания данной работы. Например, свободный резерв времени для работы 6-8 составляет:

R_{с (6-8)} = t_рн(8-9) - t_ро(6-8) = 25 – 22 = 3 дня.

Вычисленные значения резервов времени работ заносят в графы 8 и 9 таблицы.

Таким образом, все графы таблицы оказываются полностью заполненными. В таблице сконцентрированы все данные, которые можно легко сопоставить и проанализировать. При необходимости таблица может быть дополнена графами, отражающими информацию о времени свершения событий, возможных и независимых началах и окончаниях каждой работы и т.д.

Четырехсекторный метод расчета. Рассмотрим это на примере расчета одноцелевого абстрактного графика (рис.4.8.) с детерминированными оценками времени для работ при односменном режиме их выполнения.

В качестве единицы времени принят один день.

Цель расчета:

а) определить Т_кр;

б) сравнить величину Т_кр с установленным директивным сроком Т_д; привести значение Т_кр в соответствие с величиной Т_д, произвести сжатие графика;

в) после сжатия рассчитать все временные параметры для событий и работ.

Алгоритмы расчета:

наиболее раннее время свершения любого события

t_{р(i )} = макс [t_р(k) + t_(k-i)];

наиболее позднее время свершения любого события

t_{п(i )} = мин [t_р(j) – t_(i-j)].

Подготовка сетевого графика для расчета:

а) для данного этапа расчетов упорядоченная нумерация событий не требуется; однако с учетом последующей работы над графиками (оптимизация распределения ресурсов) события нумеруются упорядоченно;

б) окружность каждого события расчерчивается на четыре сектора; номер события вписывается в верхний сектор.

Рис.4.8.Расчет сетевого графика четырехсекторным методом.

Расчет графика (рис.4.8.) производится в следующей последовательности.

1) Определение Т_кр. Раннее время для события 1 принимается равным нулю. Расчет ведется непосредственно на графике с внесением значений t_{р(i )} в левый сектор i-го события; номер события, расчетом от которого получено значение t_{р(i )} , вносится в нижний сектор.

Для обеспечения четкого порядка вычислений целесообразно:

а) не возвращаться к использованной временной оценке работы для вычисления раннего времени последующего события; для последующего вычисления надо исходить из результата предыдущего расчета - раннего времени события, которое оказывается теперь уже предыдущим;

б) не записывать значения t_р(k) + t_(k-i) с целью их сравнения и нахождения максимума, если в событие i входит несколько работ, а сохранять в памяти только большее значение из сравниваемых очередных двух сумм.

Расчеты по определению Т_кр сводятся к следующим вычислениям, производимым в уме, с записью результатов непосредственно на графике.

t_р(2) = 0 + 3 = 3; (отсчет от события 1);

t_р(3) = 0 + 9 = 9; (1);

t_{р(4 )} = 0 + 15 = 15; (1);

t_р(5) = макс[(3+6); (9+11)] = 20; (3);

t_р(6) = 9 + 4 = 13; (3);

t_р(7) = макс[(9+0); (15+6)] = 21; (4);

t_р(8) = макс[(15+3); (0+12)] = 18; (4);

t_р(9) = макс[(21+7); (18+9)] = 28; (7);

t_р(10)= макс[(3+9); (20+2); (18+0); (28+0)] = 28; (9);

t_р(11) = макс[(28+3); (13+5); (28+2)] = 31; (10).

Следовательно,

Т_кр = t_р(11) = 31

Критический путь находится просмотром графика, начиная от конечного события 11. В нижнем секторе события 11 записан номер 10; это означает, что работа 10 - 11 входит в состав критического пути; она выделяется жирной линией. В нижнем секторе события 10 записан номер 9; поэтому жирной линией выделяется работа 9 - 10. Аналогичным образом определяется критический путь, вплоть до начального события 1.

В рассматриваемом примере критический путь состоит из работ: 1-4; 4-7; 7-9; 9-10; 10-11. Обозначая критический путь номерами событий, можем его записать: 1-4-7-9-11.

2) Приведение величины Т_кр в соответствие со значением Т_Д (сжатие графика). Допустим, что Т_Д = 26 дней и величина Т_кр превышает Т_Д на ∆Т= Т_кр - Т_Д = 31 - 26 = 5. Возникает задача сокращения продолжительности комплекса работ на 5 дней. Это значит, что, прежде всего на 5 дней надо сократить продолжительность работ, образующих критический путь. Однако на этом работа не всегда заканчивается, так как после сжатия критического пути 1-4-7-9-10-11 может выявиться новый критический путь, имеющий длину менее 31 дня, но более 26 дней. Тогда в свою очередь предстоит сжать работы этого нового критического пути до величины Т_Д и вновь убедиться, что в графике нет путей, превышающих директивный срок.

Сжатие графика путем безосновательного исправления временных оценок для работ создает только видимость благополучия, со сроками их выполнения и неизбежно в действительности приводит к их срыву. Поэтому все мероприятия по сжатию графика следует намечать вместе с его составителями после тщательного анализа. Рекомендуется следующий порядок такого анализа:

а) тщательно проверяют временные оценки для работ критического пути с целью устранения необоснованных завышений;

б) пересматривают технологический порядок, положенный в основу построения графика, с целью нахождения возможности параллельного проведения части критических работ;

в) рассматривают возможность сокращения длительности части работ критического пути путем применения механизации работ или более совершенных методов производства;

г) рассматривают возможность ускорения работ критического пути путем увеличения количества работающих или количества рабочих смен на этих работах.

При этом следует учитывать, что любой график характерен сходимостью работ в своей заключительной части: количество разветвлений и параллельных путей постепенно уменьшается. Поэтому, сокращая длительность отдельных работ в заключительной части графика, мы этим сокращаем общую продолжительность не только критического пути, но и многих других путей, каждый из которых может оказаться более продолжительным, чем директивный срок. Следовательно, переводя на ускоренный режим работы критического пути в очередности от конца к началу, мы упрощаем общий объем работ по сжатию графика.

В то же время следует считаться и с тем, что планирование до начала ремонта использования всех резервов ускорения в его заключительном периоде представляет известный риск. Если в заключительном периоде общего комплекса работ возникнут непредвиденные задержки, то для их компенсации в этом случае могут оказаться лишь очень ограниченные, оставшиеся неиспользованными возможности.

Анализ работ в процессе сжатия сетевых графиков упрощается и приобретает направленный характер из-за того, что зона анализа ограничивается только работами критического пути. В комплексном сетевом графике, состоящем из 5000 работ, в состав критического пути входит до 1% работ (т. е. около 50 работ), сосредоточенных в одном, двух или трех узловых графиках.

Однако, как правило, находятся и другие пути, мало отличающиеся по своей продолжительности от критического. Для уменьшения объема расчетной работы целесообразно выявить пути, продолжительность которых еще до сжатия превышает директивный срок, и подвергнуть работы на этих путях сжатию аналогично работам критического пути.

Для выявления таких подкритических путей рекомендуется следующий метод: рассматривают поочередно события критического пути от конца комплексного графика к его началу и исключают для каждого события влияние предыдущего критического события. Другими словами, для данного события t_{р(i )} определяется так, как будто бы предыдущего события k и работы k-i, лежащих на критическом пути, не было. Если получившаяся в итоге сумма t_{р(i )} окажется больше Т_Д, этот путь, определивший расчет t_{р(i )} имеет недопустимую длину и так же, как и критический, подлежит сжатию.

Таким же образом надо проконтролировать длины всех путей, которые, минуя критический путь, входят в конечные события.

Сжатие графика, изображенного на рис.4.8, на 5 дней может быть произведено следующим образом.

а) Отыскивают подкритические пути, подлежащие сжатию. Для события 11 без учета работы 10-11:

t_р(11) = макс[(13+5); (28+2)] = макс[18, 30].

18<26; следовательно, путь от события 6 до события 11 не подкритичен:

30>26; следовательно, сжатие работы 10-11 не решает задачи сокращения Т_кр до величины Т_Д .

Для события 10 без учета работы 9-10:

t_р(10) = макс[(3+9); (20+2)] = макс[12,22],

22+3=25<26; следовательно, пути, подходящие к событию 10 от событий 2 и 5, не подкритичны.

Для события 9 без учета работы 7-9

t_р(9) = 18+9 = 27,

27+3 = 30>26; следовательно, путь, идущий от события 8 к событию 9, подкритичен и подлежит сжатию на величину 4 дней.

Этот путь можно легко проследить в направлении к началу графика: 1-4-8-9-10-11. На этом заканчивается выявление подкритических путей.

6) В график после анализа всех работ вносят необходимые коррективы.

Работа 1-4 разбивается на два этапа длительностью в 7 и 8 дней, вследствие чего появляется новое событие, которому присваивается очередной порядковый номер 12.

Работа 4-7 также разделяется на два этапа, из которых первый начинается после частичного выполнения работы 1-4, т.е. после окончания работы 1-12. Новому событию присваивается очередной номер 13.

Работа 7-9 путем увеличения количества работающих или перевода ее в двух сменный режим ускоряется на 3 дня; ее новая продолжительность составит 4 дня (t_(7-9) = 4).

Аналогично до 5 дней сокращается продолжительность работы 8-9.

Все эти изменения производятся на одном и том же экземпляре сетевого графика, после чего он приобретает вид, который изображен на рис.4.9. Измененный сетевой график заново рассчитывается.

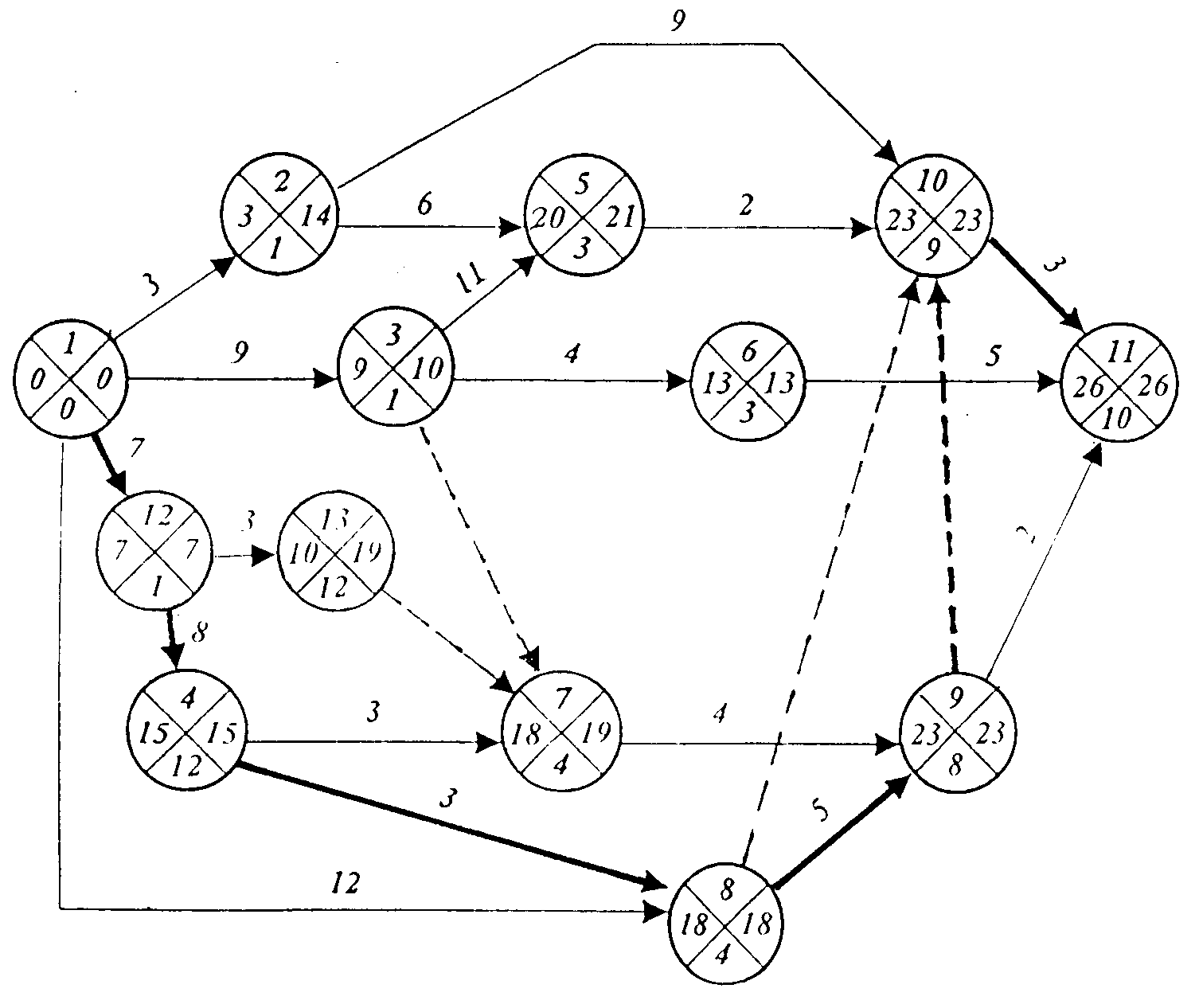
Рис.4.9.Сжатие сетевого графика.

Критический путь проходит через события 1-12-4-8-9-10-11 и Т_кр=26= Т_Д .

Сетевой график приведен к величине директивного срока.