Задания для курсовой работы по математической логике и теории алгоритмов

Вариант 1

1. На множестве М={1,2,3,…,10} заданы предикаты А(х) = "х – нечетное число"; В(х) = "х – делитель числа 60". Найти множества истинности предикатов А(х), В(х) и А(х)&В(х).

Получить высказывания из данных предикатов, добавив к ним кванторы всеобщности и кванторы существования, и определить их истинностные значения.

2. Доказать общезначимость формулы: .

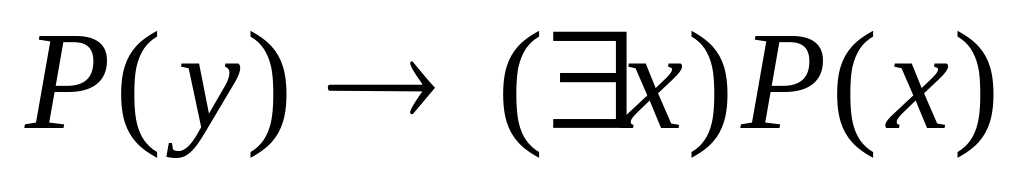3. С помощью формального языка I порядка записать определение непрерывности функции в точке. Построить отрицание полученного высказывания.

Вариант 2

1. На множестве М={1,2,3,…,10} заданы предикаты А(х) = "х – простое число"; В(х) = "х – нечетное число". Найти множества истинности предикатов А(х), В(х) и А(х)В(х).

Получить высказывания из данных предикатов, добавив к ним кванторы всеобщности и кванторы существования, и определить их истинностные значения.

2. Доказать общезначимость формулы: .

3. С помощью формального языка I порядка записать определение предела последовательности. Построить отрицание полученного высказывания.

Вариант 3

1. На множестве М={1,2,3,4,5,6,7,8} заданы предикаты А(х) = "х – простое число"; В(х) = "х – четное число". Найти множества истинности предикатов А(х), В(х) и А(х)В(х).

Получить высказывания из данных предикатов, добавив к ним кванторы всеобщности и кванторы существования, и определить их истинностные значения.

2. Доказать общезначимость формулы: .

3. С помощью формального языка I порядка записать определение неравенства треугольника. Построить отрицание полученного высказывания.

Вариант 4

1. На множестве М={1,2,3,4,5,6,7,8} заданы предикаты А(х) = "х – число, кратное 3"; В(х) = "х - 4 > 0". Найти множества истинности предикатов А(х), В(х) и В(х)А(х).

Получить высказывания из данных предикатов, добавив к ним кванторы всеобщности и кванторы существования, и определить их истинностные значения.

2. Доказать общезначимость формулы: .

3. С помощью формального языка I порядка записать определение наибольшего значения функции на отрезке. Построить отрицание полученного высказывания.

Вариант 5

1. На множестве М={2,3,4,6,8} заданы предикаты P₁(х,y) = "х делится на y"; P₂(х,y) = "х + y = 10". Найти множества истинности предикатов P₁(х,y), P₂(х,y) и P₁(х,y)&P₂(х,y).

Получить высказывания из данных предикатов, добавив к ним кванторы всеобщности (по всем переменным) и кванторы существования, и определить их истинностные значения.

2. Доказать общезначимость формулы: .

3. С помощью формального языка I порядка записать определение монотонно возрастающей функции. Построить отрицание полученного высказывания.

Вариант 6

1. На множестве М={0,1,2,3,4,6,8} заданы предикаты P₁(х,y) = "х > 4y"; P₂(х,y) = "х² + y² = 4". Найти множества истинности предикатов P₁(х,y), P₂(х,y) и P₁(х,y)P₂(х,y).

Получить высказывания из данных предикатов, добавив к ним кванторы всеобщности (по всем переменным) и кванторы существования, и определить их истинностные значения.

2. Доказать, что формула 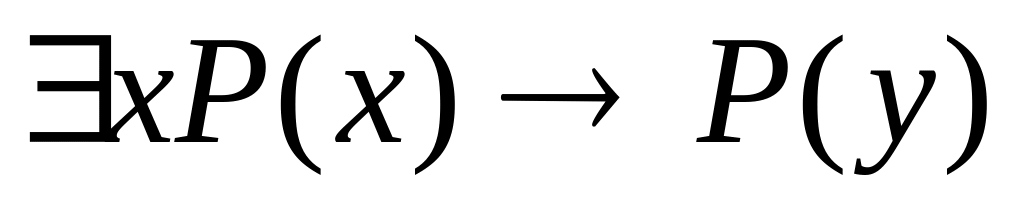не общезначимая.

3. С помощью формального языка I порядка записать определение транзитивности операции "больше" на множестве целых чисел. Построить отрицание полученного высказывания.

Вариант 7

1. На множестве М={0,1,2,3,4,5,6} заданы предикаты P₁(х,y) = "х + y = 5"; P₂(х,y) = "х - y > 4". Найти множества истинности предикатов P₁(х,y), P₂(х,y) и P₁(х,y)&P₂(х,y).

Получить высказывания из данных предикатов, добавив к ним кванторы всеобщности (по всем переменным) и кванторы существования, и определить их истинностные значения.