1. Вероятностный метод

Инструментом для проведения вычислений является математическая теория вероятностей. Каждому событию ставится в соответствие некоторая величина, характеризующая то, что это событие произойдет – вероятность данного события р. Если событие не может произойти ни при каких условиях, от вероятность р=0. Если событие происходит при любых условиях, то его вероятность р=1. Если же в результате проведения эксперимента выясняется, что событие происходит в n случаях из N, то вероятность р=n/N. Сумма вероятностей всех событий, которые могут произойти в результате некого эксперимента должна быть равна единице. Перечисление всех возможных событий с соответствующими им вероятностями называется распределением вероятностей в данном эксперименте. Например, при бросании игральной кости вероятность выпадения числа 7 равна 0. Вероятность выпадения одного из числе от 1 до 6 равна 1. Для каждого из числе от 1 до 6 вероятность его выпадения равна р=1/6.

Распределение вероятностей в данном случае выглядит так

1 – 1/6, 2 – 1/6, 3 – 1/6, ……6 – 1/6.

Вероятность можно выразить в процентах - р=(n/N) 100%, тогда вероятность находится в пределах от 0% до 100%.

Рассмотрим в качестве примера два финансовых проекта А и В, для которых возможные нормы доходности IRR находятся в зависимости от будущего состояния экономики. Данная зависимость отражена в след таблице

Данные для расчета ожидаемой нормы доходности

вариантов вложения капитала в проекты А и В

Состояние Вероятность Проект А Проект В

Экономики данного состояния IRR IRR

Подъем р1=0,25 90 % 25%

Норма р2=0,5 20% 20%

Спад р3=0,25 -50% 15%

Для каждого из проектов А и В может быть рассчитана ожидаемая норма доходности ERR - средневзвешенное (где в качестве весов берутся вероятности) или вероятностное среднее возможных IRR.

ERR = , (1)

где n- число возможных ситуаций.

Для проектов А и В по формуле (1) получаем

ERR = 025 х 90% + 0,5 х 20% + 0,25 х (-50%) = 20%

ERR = 0,25 х 25% + 0,5 х 20% + 0,25 х 15% = 20%

Таким образом, для двух рассматриваемых проектов ожидаемые нормы доходности равны, несмотря на то, что диапазон возможных значений IRR сильно различаются – у проекта А от –50% до 90%, у проекта В – от 15% до 25%.

Распределение вероятностей для проектов А и В (*)

0,5 0,5

0,4 0,4

0,3 0,3

0,2 0,2

0,1 0,1

-50 20 90 IRR(%) 15 20 25 IRR(%)

М ы предположили, что возможны три состояния экономики - норма, спад и подъем. В реальности же состояние экономики может меняться от самой глубокой депрессии до наивысшего подъема с множеством промежуточных положений. Как правило, среднему (нормальному) состоянию соответствует наибольшая вероятность, далее значение вероятностей равномерно уменьшаются при удалении от нормы как в одну (подъем), так и в другую (спад) сторону, стремясь к нулю в крайних положениях, соответствующих полной депрессии и наибольшему подъему. Если величина доходности, соответствующая нормальному положению экономики является средним арифметическим двух своих крайних значений, то мы получим распределение, которое в теории вероятностей носит название «нормального» и графически изображается так

Р

ERR

Нормальное распределение достаточно полно отражает реальную ситуацию и дает возможность, используя ограниченную информацию, получать числовые характеристик, необходимых для оценки степени риска того или иного проекта. Далее будем предполагать, что мы всегда находимся в условиях нормального распределения вероятностей.

На рисунке (*) приведены графики распределения вероятностей для проектов А и В (они удовлетворяют условиям нормального распределения). Предполагается, что для проекта А в наихудшем случае убыток составит не более 50%, а в наилучшем случае доход не превысит 90%. Для проекта В - 15% и 25% соответственно.

Р

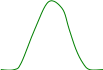
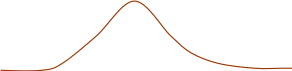
-50 20 90 ERR

Чем более сжат график, тем выше вероятность, соответствующая среднему ожидаемому доходу ERR,и вероятность того, что величина реальной доходности окажется достаточно близкой к ERR. Тем ниже будет и риск, связанный с соответствующим проектом. Поэтому меру сжатости графика можно принять за достаточно корректную меру риска.

Меру сжатости определяет величина, которая в теории вероятности носит название «среднеквадратичное отклонение» - и рассчитывается по формуле

Чем меньше величина , тем больше «сжато» соответствующее распределение вероятностей и тем менее рискован проект. Рассчитаем значение сигма для наших примеров.

Проект А

=

Проект В

=

Как видно, для первого проекта велико значение отклонения ожидаемой доходности от нормального значения, для второго такое отклонение очень невелико. Следовательно, проект А гораздо более рискованный. Считается, что среднерисковой операции соответствует значение около 30%.

В рассмотренном примере распределение вероятностей предполагалось известным заранее. Но очень часто бывают доступны лишь данные о том, какой доход приносила некая финансовая или хозяйственная операция в предыдущие годы. Например, доступная информация может быть представлена в следующем виде:

Динамика IRR

год IRR

1995. 10 %

1996. 8 %

1997. 0

1998. 15 %

В этом случае для расчета среднеквадратичного отклонения используется такая формула:

=

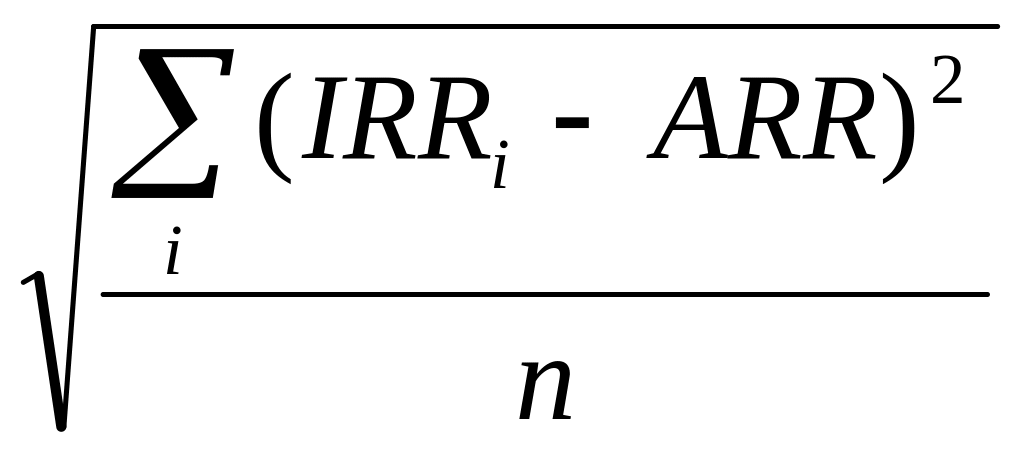
Здесь n - число лет, за которые приведены данные, а ARR - среднее арифметическое всех IRR за n лет - рассчитывается по формуле

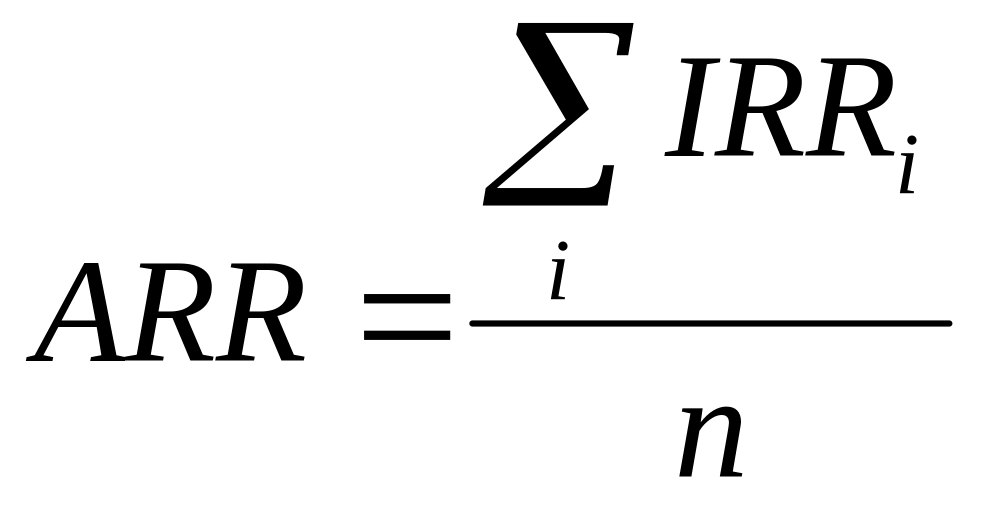
Для нашего примера получаем ARR = (10 + 8+15)/4 = 8,25%,

= .

Еще одна величина, характеризующая степень риска, является коэффициент вариации CV. Он рассчитывается по следующей формуле

и выражает количество риска на единицу доходности. Чем выше этот коэффициент, тем выше степень риска.

Для наших примеров коэффициенты вариации равны

проект А - CV = 49,5 / 20 = 2,475

проект В - CV = 3,5 / 20 = 0,175.

Коэффициент вариации позволяет сравнивать колеблемость, т.е. степень отклонения признаков, имеющих разные единицы измерения. Чем выше коэффициент вариации, тем сильнее колеблемость признака. Установлена следующая оценка коэффициентов вариации:

до 10% — слабая колеблемость;

10-25% — умеренная колеблемость;

свыше 25% — высокая колеблемость.

Вероятностная оценка риска математически достаточно разработана, но опираться только на математические расчеты в предпринимательской деятельности не всегда бывает достаточным, так как точность расчетов во многом зависит от исходной информации.