5. Расчет реакции цепи при одиночных входных сигналах.

В данном разделе рекомендуется использовать операторный метод анализа электрических цепей [5]. Изображение искомой реакции на выходе F₂(s) определяем по выражению

F₂(s)=F_I(s)H(s).

Последнему соотношению во временной области соответствует ин­теграл наложения

Для получения изображения одиночных импульсов может быть использована теорема запаздывания.

Рассмотрим, например, прямоугольный импульс напряжения рис.7.

f1(t)

FM

0 t

Рис.7

Изображение этой суммы с учетом теоремы запаздывания равно

Реакция на выходе цепи находится с помощью теоремы разложе­ния для конкретного случая полюсов F₂(s).

13

6.Определение амплитудно-частотных и фазо-частотных характеристик цепи.

Входные и передаточные функции цепи представляют собой рацио­нальные функции переменной S

где M(s),N(s) – полиномы. При подстановке s=jω получим

Зависимость модуля |H(jω)| от ω, т.е.

называется амплитудно-частотной характеристикой цепи, а φ(ω)= φ_M(ω) - φ_N(ω) – фазо-частотной характеристикой цепи.

7.Определение спектров входного и выходного сигналов в виде одиночных импульсов

Спектр импульсного сигнала находят по изображению сигнала, используя связь преобразований Лапласа и Фурье. Для одиночного импульса напряжения u_I(t), имеющего изображение U₁(s), комплексный спектр составит

Модуль функции U₁(jω) определяет амплитудный спектр A₁(ω), а аргумент U₁(jω)-фазовый спектр φ₁(ω)

Так, например, для сигнала в виде прямоугольного импульса получим комплексный спектр

Амплитудный спектр

При A1=0 , где k=±1,±2…

14

Фазовый спектр

Графики амплитудного и фазового спектра показаны на рис.8.

Спектр выходного сигнала определяется с учетом частотных характеристик цепи.

,

где , - амплитудный и фазовый спектр выходного сигнала соответственно.

Откуда следует, что

A2(ω)=A1(ω)•A(ω) ,

2(ω)= 1(ω)+ (ω).

При построении графиков спектров их целесообразно изобразить на одном рисунке

15

8.Расчет вынужденного режима при несинусоидальном периодическом воздействии.

При рассмотрении этого режима сигнал на входе цепи представляют в виде периодической последовательности заданных в условии задачи импульсов. Период Т принимают равным Т-nτ, где τ- длительность импульса, а величина n и форма импульса ука­заны в таблице вариантов.

Для нахождения комплексных амплитуд Аk периодического сигнала f1(t) можно использовать соотношение, связывающее величины Аk с изображением одиночных импульсов F1(s), совпадающее с периодической функцией f1 (t) в пределах периода [0;T].

Известно, что комплексные амплитуды определяются соотношением

где

Очевидно, что связь Аk с комплексным спектром будет аналогичной:

определим комплексные амплитуды для периодической последовательности прямоугольных импульсов длительностью

При k=0 A= τF

k=1

k=2

k=3 и т.д.

Переходя во временную область, получим ряд Фурье в виде

.

По полученным выражениям комплексных амплитуд могут быть пост­роены амплитудный и фазовый спектр периодического сигнала.

Для нахождения действующего значения напряжения используют формулу [8]

16

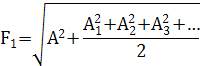
Для получения комплексного спектра выходного сигнала исполь­зуют соотношение

.