3.Переходная и импульсная характеристики цепи

Переходная характеристика h_I(t) представляют собой реакцию цепи при нулевых начальных условиях на воздействие сигнала в виде единичной ступенчатой функции δ₁(t). Так, например, в цепи с источ­ником напряжения на входе переходная характеристика для выходного напряжения имеет изображение H_U(s)/S, откуда

, (2)

где L^-1 -символ обратного преобразования Лапласа.

Импульсная характеристика h(t) представляет собой реакцию цепи при нулевых начальных условиях на сигнал в виде еди­ничной импульсной функции δ(t), изображение которой L{δ(t)}=1. Таким образом, импульсная характеристика для выходного напряжения U₂(t) в цепи с источником напряжения будет

h(t)=L^-1{H_U(S)} , (3)

В цепи с источником тока в выражение (2),(3) следует подста­вить Hi(а)

9

вместо H_U(s).

Для проверки полученных соотношений можно использовать выра­жение обобщенной производной, связывающие h(t) и (t)

(4)

В выражении (4) степени полинома числителя и знаменателя мо­гут оказаться одинаковыми. В этом случае h(t) может содержать в качестве слагаемого импульсную функцию.

4.Система уравнений по методу пространства состояний

Описание цепи в виде системы дифференциальных уравнений:

называют системой уравнений по методу пространства состояний.

Уравнение (5) называют уравнением состояния, а уравнение (6) – выходным уравнением. Здесь

x(t) – вектор переменных состояний;

y(t) – вектор реакций цепи;

u(t) – вектор входных воздействий.

В линейном случае уравнение (5) можно записать в виде

В качестве переменных состояния принимают непрерывные функции (напряжение на емкостях или ток на индуктивностях). Одним из простейших методов формирования уравнения (7) является сле­дующий прием [1]. На основании теоремы замещения ин­дуктивности заменяют на источники тока i_L(t), а емкости на источ­ники напряжения u_C(t). В результате получаем резистивную цепь с источниками и внешними воздействиями. Затем проводится анализ цепи, при этом определяются напряжения на индуктивностях u_L(t) и токи на емкостях i_C(t). Производя перегруппировку членов, находят уравнение (7) следующие ключевые выражения

10

Рассмотрим пример формирования уравнений по методу пространст­ва состояний. Обратимся к цепи, показанной на рис.5.

Рис.5

Заменим ветви с реактивными элементами, соответствующими ис­точниками напряжения и тока.

Рис.6

На основании законов Кирхгофа и получим следующую систему уравнений

Или, используя (8), (9), получим

11

Откуда матрицы А и В из выражения (7) будут для цепи на рис. 5.

A= ,

Если принять, что выходной реакцией является, например, ток в резисторе R_2. то система (6) сводимая к

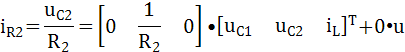
Таким образом, матрицы C и D имеют вид

Решение уравнения (6) во временной области имеет вид

где e^At – матричная экспонента, x(0) – вектор начальных условий.

Первое слагаемое (10) отвечает реакции при нулевом входе, а второе при нулевых начальных условиях. Таким образом, выражение (10) есть сумма свободной и вынужденных составляющих реакции. Исходя из определения импульсной характеристики, то есть при x(0), u(t)=δ(t), получим из (10) и (5)

Таким образом, в приведенном примере импульсная характеристика для тока будет

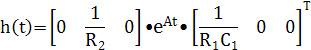
Преобразуем по Лапласу (6), (7) при нулевых начальных условиях

SX(s)=AX(s) + BU(S)

Y(s)=CX(s) + DU(s)

Функция цепи связана с описанием по методу переменных состояний следующим образом

12