3.4. Імпульсні характеристики ідеальних цф

Аналітичні описи імпульсних характеристик ЦФ різного типу виходять в загальному випадку шляхом виконання зворотного перетворення Фур'є їх ідеалізованих частотних характеристик ЧХ Hd (jω).

Для ідеального цифрового ФНЧ, як показано вище, імпульсна характеристика визначається виразом

; , n= (1, (2, .,

(3.13)

Для ідеального всепропускаючого фільтру (ВПФ) сигнал на виході співпадає з сигналом на вході:

y(n) = x(n); hd(0) =1; hd (n) =0 при n 0; .

(3.14)

Імпульсні характеристики ЦФ типів ФВЧ, СФ (смугового), РФ (режекторного) і БСФ (багатосмугового) можуть бути виражені через імпульсні характеристики цифрового ФНЧ і ВПФ :

,	(3.15)
,	(3.16)
,	(3.17)

де Hd (jω) ФНЧ, Hd (jω) ФНЧ1 і Hd (jω) ФНЧ2 - частотні характеристики ідеальних ФНЧ з частотами зрізу λзр, λзр1, λзр2, (λзр2> λзр1), що відповідають частотам зрізу ФВЧ, СФ і РФ.

Такий же зв'язок справедливий і для імпульсних характеристик, що дозволяє безпосередньо записати аналітичні вирази, що відповідають їм:

, , n= ±1, ±2, .	(3.18)
, ,	(3.19)
, .	(3.20)

Аналогічним чином знаходяться співвідношення і для конкретного БСФ.

4. Розрахунок кіх-фільтрів методом частотної вибірки

4.1. Особливості розрахунку методом частотної вибірки

У методі частотної вибірки імпульсна характеристика фільтру h (n) N знаходиться шляхом дискретизації по частоті заданої частотної характеристики Hd (j ω) і обчислення її зворотного дискретного перетворення Фур'є (ЗДПФ).

Дискретизація частотної характеристики Hd (j (ω) по частоті здійснюється в смузі 0 ... ω_д шляхом переходу від безперервних значень частоти ω до дискретних: _ωk=∆ω (k, де k=0, 1, ..., N − 1; ∆ω₌ωд/N − крок дискретизації; k − номер частотної вибірки; N − число точок дискретизації.

Крок дискретизації по частоті ∆ω вибирається з умови ∆ω≤∆ω_пер/ (L+1), де L− цілі числа, L = 0, 1, 2, ...; ∆ω_пер − перехідна смуга фільтру.

В результаті виходить дискретизована частотна характеристика фільтру (ДЧХ) (рис. 3.4). Оскільки задана частотна характеристика відповідає фільтру, що фізично не реалізовується, з нульовим запізнюванням, то для ЦФ із сходинкоподібними АЧХ дискретизована частотна характеристика ототожнюється далі з їх дискретизованою АЧХ.

Дискретизація частотної характеристики на рис. 4 виконана з кроком ∆ω=∆ω_пер/2 (L=1).

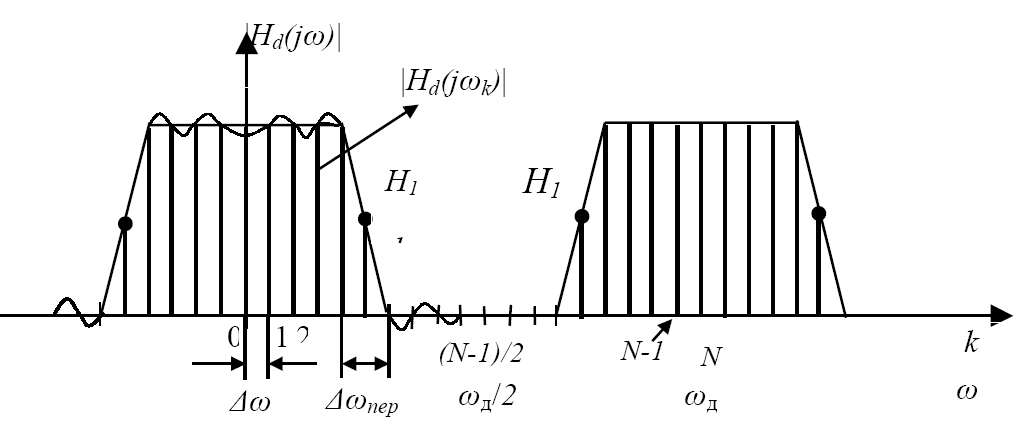
Рис. 4. Дискретизованао ЧХ цифрового фільтру нижніх частот

ДЧХ має значення, рівні в смузі пропускання 1 (Hd (j ω_k)=1), в смузі затримки − нулю (Hd (j ω_k)=0) і в перехідній смузі, - деяким проміжним варійованим (оптимізованим) значенням Hd (j (ω_k) = H1 = var, від яких залежить якість апроксимації заданої частотної характеристики.

ДЧХ Hd (j ω_k) можна поставити у відповідність деяку імпульсну характеристику hp (n), визначувану за допомогою зворотного дискретного перетворення Фур'є (ЗДПФ):

.

Отримана імпульсна характеристика (рис. 3.5.а) є періодичною з періодом Np=N, оскільки дискретизації в частотній області відповідає періодизація в часовій області.

В якості імпульсної характеристики що синтезується методом частотної вибірки НРЦФ вибирається один період імпульсної характеристики hp (n), зрушений управо на (N − 1) /2 відліків (для забезпечення фізичної, що реалізовується) і усічений прямокутною ваговою функцією (для отримання КІХ-фільтру) (рис. 3.5.б) :

.

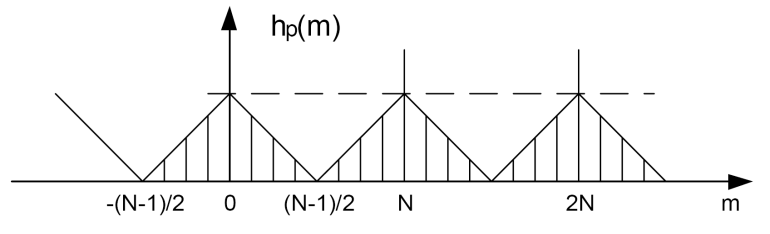
а)

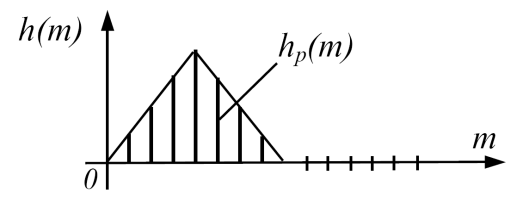
б)

Рис. 5. Імпульсна характеристика, відповідна ДЧХ (а) і імпульсна характеристика НРЦФ, синтезованого методом частотної вибірки (б)

За імпульсною характеристикою h (n) знаходиться частотна характеристика фільтру H (j ω), що апроксимує задану Hd (j ω):

АЧХ фільтру на частотах ω=ωk: H (ωk) =Hd (ωk) точно співпадає з частотними вибірками ДЧХ, а на частотах ω≠ωk H (ω) ≠Hd (ω) − відрізняється від заданої на величину похибки апроксимації. ФЧХ фільтру строго лінійна внаслідок симетрії імпульсної характеристики.

Якість апроксимації в цьому методі залежить від числа вибірок частотної характеристики в перехідній смузі L і їх значень H_i._{опт (}i=1,2,...,L), що роблять функцію, що апроксимується, гладшою.

Різним значенням L відповідають наступні зразкові значення максимального рівня бічних пелюсток :

L = 0 : δ_2мах ≈ − 20 дБ;

L = 1 : δ_2мах ≈ − 40 дБ;

L = 2 : δ_2мах ≈ − (50 − 60) дБ;

L = 3 : δ_2мах ≈ − (80 − 100) дБ.

Реально методом частотної вибірки можна синтезувати НРЦФ з мінімальним згасанням в смузі затримання до (90 − 120) дБ.

Таким чином, оптимізація фільтру полягає у виборі L − числа вибірок в перехідній смузі і пошуку їх оптимальних значень Hi._опт, що мінімізують похибки апроксимації. Очевидно, що зі збільшенням числа варійованих вибірок істотно ускладнюється процедура оптимізації. Вона досить ефективно реалізується на ЕОМ методом лінійного програмування.