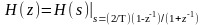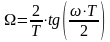ЛАБОРАТОРНА РОБОТА №2

ПРОЕКТУВАННЯ ЦИФРОВОГО ФІЛЬТРУ

МЕТОДОМ БІЛІНІЙНОГО ПЕРЕТВОРЕННЯ В ПАКЕТІ ПРОГРАМ MATHCAD

Мета роботи

1. Вивчити методи білінійного перетворення і різних видів апроксимації фільтрів-прототипів.

2. Синтезувати передатну функцію цифрового фільтру (ЦФ) по аналоговому прототипу методом білінійного перетворення.

3. Дослідити перехідну і амплітудно-частотну (АЧХ) характеристику фільтру.

Короткі теоретичні відомості

1. Завдання і методи синтезу цифрових фільтрів

Синтез ЦФ в загальному випадку включає синтез передатної функції і структури фільтру по заданій його частотній або імпульсній характеристиці, а також оцінку необхідної розрядності чисел для коефіцієнтів фільтру і відліків вхідного, вихідного і внутрішніх сигналів.

Синтез передатної функції ЦФ H(z) за заданою частотною характеристикою H_d(jω) полягає в її апроксимації і визначенні коефіцієнтів передатної функції. Методи синтезу розділяються на аналітичні, ітераційні і чисельні.

По виду апроксимованої частотної характеристики Hd(jω) розрізняють цифрові фільтри із ступінчасто-подібною амплітудно-частотною характеристикою (АЧХ) - фільтри нижніх частот (ФНЧ), верхніх частот (ФВЧ), смуго-пропускаючі (СПФ), смуго-загороджуючі (СЗФ), багатосмугові (БСФ) (рис. 2.1) і ЦФ з довільною частотною характеристикою. Можуть бути синтезовані також ЦФ з частотною характеристикою цифрового диференціатора і перетворювача Гільберта.

Оскільки частотні характеристики ЦФ періодичні по частоті з періодом ω_д і їх модуль (АЧХ) і аргумент (ФЧХ) мають властивості відповідно до парної і непарної симетрії відносно частот ω = 0 або ω_д/2, то їх достатньо задати в смузі частот (0 – ω_д/2) або смузі (0 – π) нормованих частот λ= ωT_д (рис. 2.1).

Початковими даними для синтезу ЦФ за заданою частотною характеристикою (рис.2.1) є:

• частоти зрізу ω_зр, затримки ω_з, що визначають межі і значення смуг пропускання, затримки і перехідних смуг фільтру;

• допустима нерівномірність АЧХ фільтру в смузі пропускання (чи послаблення на межах смуги пропускання у разі монотонних АЧХ) А_П, дБ;

• мінімальне згасання АЧХ в смузі затримки А_З, дБ.

Параметрам А_П, А_З, що визначають допустимі похибки апроксимації заданої ідеалізованої АЧХ |Hd (jω)|, відповідають на рис. 2.1 рівні припустимого відхилення розрахункової АЧХ |H(jω)| від 1 в смузі пропускання (1 - δ₁) і від нуля в смузі затримання δ₂: А_П = 20(lg[1/(1 -δ₁)], дБ; А_З = 20(lg(1/δ₂), дБ.

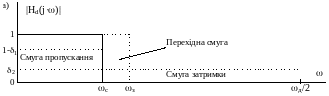
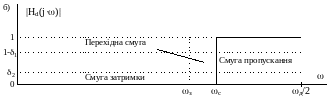
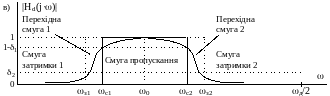
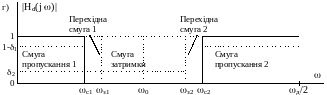
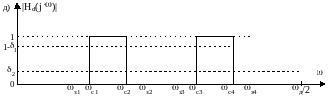
Рис. 2.1. Приклади завдання АЧХ ЦФ

Виділені на рис. 2.1 пунктиром області утворюють поле допусків на похибки апроксимації, в які повинна укластися розрахункова апроксимуюча АЧХ |H(jω)|, показана на рис. 2.1, в.

2. Метод білінійного перетворення

Метод білінійного перетворення відноситься до аналітичних методів розрахунку.

По методу білінійного перетворення ЦФ, що синтезується, ставиться у відповідність деякий аналоговий фільтр-прототип (АФП) з передатною функцією Н(s) і частотною характеристикою H(jΩ), однозначно пов'язаними з передатною функцією H(z) і частотною характеристикою H(jω) ЦФ:

АФП ЦФ АФП ЦФ

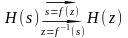
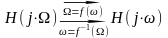
Зв'язок цей визначається прямою s = f(z) і зворотною z = f^-1(s) перетворюючими функціями і відповідні ним при s = jΩ і z = e^jωTд перетвореннями частот Ω = f(ω), ω = f ^{- 1}(Ω) аналогового і цифрового фільтрів.

За допомогою цих перетворень визначаються вимоги до АФП, по яких розробленими методами синтезується його передатна функція H(s), що перетворюється потім в шукану передатну функцію ЦФ H (z).

Білінійне перетворення, яке визначається таким чином:

S = f (z) = (2/T)[(1 - z - 1) / (1+z - 1)]

(2.1)

Можна також знайти зворотне співвідношення

z – 1 = [ (2 - sT) / (2+sT)]

(2.2)

З властивостей процедури переходу на основі білінійного перетворення витікає, що уявна вісь S-площини відображається в одиничне коло в Z-площини (де |z|=1).

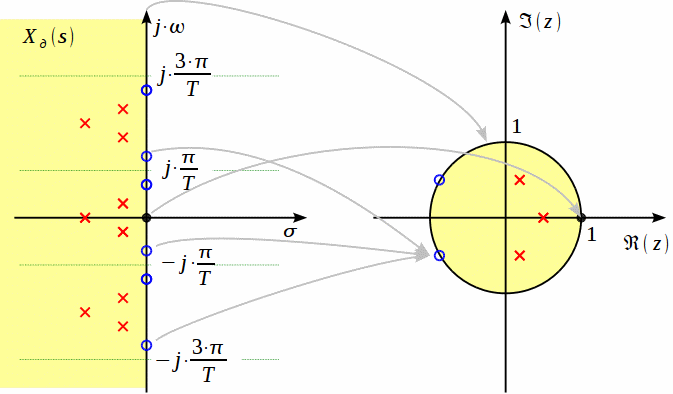
Рис. 2.2. Властивості процедури переходу на основі білінійного перетворення

Білінійне перетворення - однозначна функція. Це означає, що кожній точці в Z-площини відповідає одна точка в s-площині і навпаки. З цієї властивості однозначності виходить, що відсутній ефект накладання спектрів при білінійній процедурі відображення.

Методика розрахунку цифрових фільтрів на основі методу білінійного перетворення включає знаходження відповідної передатної функції Н(s) аналогового фільтру і застосування до неї білінійного перетворення для отримання передатної фікції H(z) потрібного цифрового фільтру

(2.3)

При цьому перетворенні зберігатимуться і частотні характеристики, і властивості стійкості аналогового фільтру. Проте це не означає, що частотні характеристики аналогового і цифрового фільтру ідентичні, однакова тільки їх «форма». Наприклад, якщо амплітудно-частотна характеристика аналогового фільтру монотонно спадає при 0 <  < , то відповідний цифровий фільтр, отриманий за допомогою співвідношення (2.3), володітиме монотонно спадаючою АЧХ при 0 <  < ,. Тобто, якщо АЧХ аналогового фільтру має k підйомів і спадів при 0 <  < , то і амплітудно-частотна характеристика відповідного цифрового фільтру матиме k підйомів і спадів.

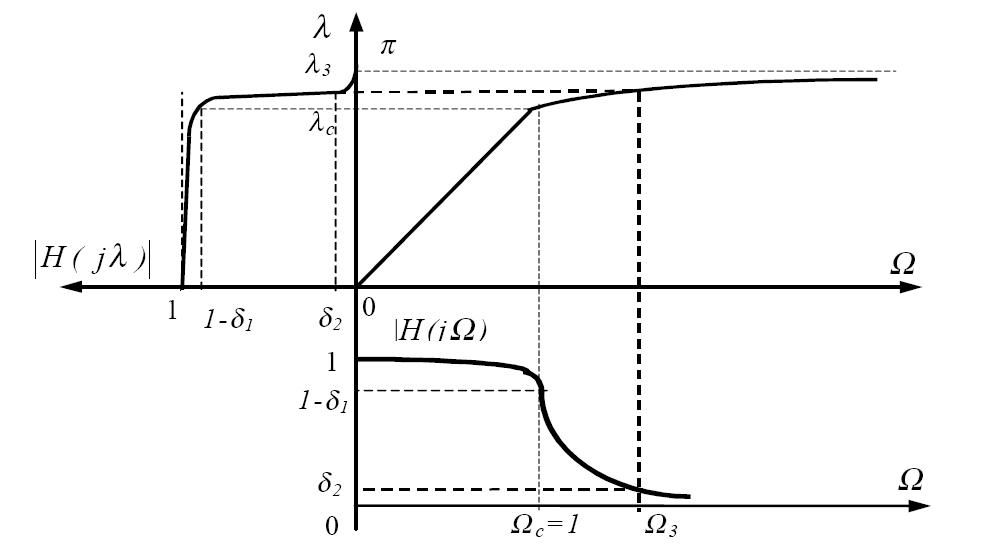
Рис. 2.3. Перетворення АЧХ аналогового ФНЧ в АЧХ цифрового ФНЧ

В результаті переходу до нормованих частот ЦФ частотні перетворення приймають вигляд

(2.4)

Характер деформації частот при білінійному перетворенні показаний на рис. 2.3.

Для забезпечення рівності 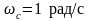необхідно деформувати частоту аналогового ФНЧ - прототипу: .

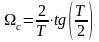Білінійне перетворення забезпечує просту процедуру переходу від аналогових до цифрових фільтрів і зберігає вид частотних характеристик при перетворенні. Це означає, що широкосмугові аналогові фільтри з крутою перехідною областю відображаються в широкосмугові цифрові фільтри без ефекту накладання. У цьому полягає основна перевага цього методу в порівнянні з методом інваріантності імпульсної характеристики. Недоліком білінійного перетворення є те, що нелінійність співвідношення між цифровою частотою  і аналоговою частотою Ω призводить до спотворення частотних характеристик аналогових фільтрів. Крім того, при цьому перетворенні не зберігається імпульсна характеристика.