1. Базисные строки (и столбцы) линейно- независимы.

2. Все остальные строки (и столбцы) матрицы являются линейными комбинациями базисных строк (столбцов).

Доказательство.

1). Рассмотрим базисный минор (напомним, базисный минор не равен нулю). Предположим, что базисные строки линейно-зависимы. Тогда по Теореме 4. одна из строк является линейной комбинацией остальных строк. Вычитая линейную комбинацию из этой строки, мы получим нулевую строку. В результате базисный минор равен нулю, а это противоречит условию, что базисный минор не равен нулю. Поэтому базисные строки не могут быть линейно-зависимыми. Следовательно, строки базисного минора линейно- независимы. Первое свойство доказано.

2). Рассмотрим матрицу , у которой и - базисный минор. Допустим, что базисный минор расположен в левом верхнем углу . Рассмотрим еще один минор . Надеюсь для читателя очевидно, что он равен нулю. Если для Вас этот факт не очевиден, советую перечитать определение базисного минора.

Этот минор равен нулю при всех значениях и . Разложим этот минор по столбцу :

,

Очевидно . Следовательно

,

или

Таким образом, строка является линейной комбинацией базисных строк.

Теорема доказана.

ЛЕКЦИЯ 4

Линейное (векторное) пространство. Примеры линейных пространств. Линейная зависимость. Теорема о линейной зависимости. Базис и размерность линейного пространства. Примеры базисов.

«Часто приходится встречаться с объектами, над которыми производятся операции сложения и умножения на числа»

Линейное (векторное) пространство.

Рассмотрим некоторое множество , состоящее из элементов произвольной природы.

Замечание. Когда в математике говорят об элементах произвольной природы, то предполагают, что эти элементы имеют математическую природу. Это могут быть числа, векторы, матрицы, тензоры, спиноры, функции, полиномы, функционалы и т.д.

Пусть в определены операция сложения двух элементов и , обозначаемая и операция умножения элемента на число α, обозначаемая α .

Символическая запись этих операций:

Операция сложения: ,

Операция умножения: .

Символом обозначается декартово произведение множества на множество , (т.е. само на себя). Символом обозначается декартово произведение множества на множество , где - множество вещественных чисел.

О декартовом произведении множеств: Декартово произведение множества и множества , это такое множество, которое состоит из пар элементов , первый из которых принадлежит первом множеству , второй – второму множеству .

Примерами операций сложения и умножения являются хорошо знакомые операции сложения и умножения обычных вещественных чисел, операции сложения трехмерных векторов и умножения вектора на число, операции сложения матриц и умножения матрицы на число, сложения функций и умножения функции на число и т.п.

Эти операции можно задать различными способами, но с одним условием, чтобы они обладали определенным набором свойств (или аксиом), которые мы определим ниже. Причем эти свойства мы постулируем, то есть cчитаем их аксиомами.

Употребляемые нами термины - умножение и произведение, мы считаем эквивалентными.

Дадим строгое определение линейного пространства.

ОПРЕДЕЛЕНИЕ. Множество элементов произвольной природы называется линейным пространством, а его элементы векторами, если в нем определены следующие две операции:

а) операция сложения векторов (правило сложения или закон сложения), по которому любым двум векторам и из сопоставляется некоторый вектор , называемый их суммой и обозначаемый

б) операция произведения вектора на число, по которому вектору из и вещественному числу α сопоставляется некоторый вектор из , называемый произведением вектора на число и обозначаемый

.

Для этих операций должны быть выполнены следующие 8 аксиом:

Существует вектор такой, что для каждого из выполнено равенство . Для каждого вектора существует вектор , такой что .

5. 6. 7. 8.

Вектор в аксиоме 3 называется нулевым вектором. Вектор в аксиоме 4 называется вектором, противоположным вектору .

Если в пункте б) определения линейного пространства мы рассматриваем вещественные числа , то в этом случае называется вещественным линейным пространством. Если же рассматриваются комплексные числа , то линейное пространство называется комплексным (или унитарным) линейным пространством.

Линейное пространство является также и группой (см. Теория групп).

Рассмотрим различные числовые множества – множество вещественных чисел, комплексных чисел, множество строк из вещественных (или комплексных) чисел, множество матриц, множество полиномов, множество функций и т.д. В каждом из этих множеств хорошо нам известны обычные операции сложения и произведения на числа.

Эти множества дают нам примеры линейных пространств.

Примеры линейных пространств:

1. . Множество вещественных чисел является вещественным линейным пространством с обычными операциями сложения и умножения вещественных чисел. Проверьте выполнимость аксиом!

2. . Множество комплексных чисел является комплексным (или унитарным) линейным пространством с обычными операциями сложения и умножения комплексных чисел. Проверьте выполнимость аксиом!

3. . Множество состоит из строк длиной вида , где - вещественные числа. Введем операции сложения строк и умножения строки на числа. Мы получим пространство известное, как - мерное координатное пространство (см. математический анализ, теоретическая физика).

4. . Множество образуют полиномы от одной переменной , степень которых не выше заданного натурального числа , вида

.

Множество полиномов является вещественным линейным пространством. Действительно, сумма двух полиномов степени есть полином степени не выше , произведение полинома на вещественное число также является полиномом и принадлежит данному множеству полиномов. Таким образом, всякий полином является вектором линейного пространства.

5. . Существует линейное пространство , состоящее из одного вектора. Такое пространство называется нулевым. Единственный вектор этого пространства, по необходимости, оказывается нулевым вектором и самому себе противоположным.

6. . Множество состоит из функций от одной независимой переменной , определенных и непрерывных на отрезке . Множество функций также образует линейное пространство, причем функция будет являться вектором этого пространства. Действительно, любым двум функциям и и числу можно сопоставить их сумму и произведение в обычном смысле слова

,

.

Роль нулевого вектора играет нулевая функция. Можно без труда проверить, что все аксиомы выполнены.

7. . Множество матриц порядка является линейным пространством. Действительно, сумма двух матриц и равна некоторой третьей матрице , произведение матрицы на число есть также некоторая матрица :

Важное замечание. Рассмотренные нами выше семь примеров линейных пространств, показывают, что понятие вектор является универсальным понятием, в роли которого могут выступать различные математические объекты – числа, векторы, строки, столбцы, матрицы, функции, полиномы, операторы (см. ниже) и т.д.

Линейная зависимость. Теорема о линейной зависимости.

Начнем с замечания. Определения линейной комбинации векторов, тривиальной и нетривиальной системы векторов, линейной зависимости системы векторов, а также теоремы о линейной зависимости полностью идентичны утверждениям относительно строк (столбцов) матрицы.

Пусть – линейное пространство.

Рассмотрим в некоторую конечную систему векторов .

Введем следующие понятия. Выражение:

(1)

называется линейной комбинацией этой системы векторов, коэффициенты являются числами, которые выбираются произвольно.

Введум следующие понятия о тривиальной и о нетривиальной линейной комбинации:

• Линейная комбинация (1) называется тривиальной, если мы рассматриваем случай, когда все коэффициенты равны нулю: .

• Линейная комбинация (1) называется нетривиальной, если среди коэффициентов есть ненулевые, т.е. достаточно, чтобы один из коэффициентов не равнялся нулю.

При образовании линейной комбинации мы вправе выбирать произвольные наборы значений коэффициентов. Если мы выбираем набор нулевых коэффициентов, то линейная комбинация векторов является тривиальной, для ненулевых коэффициентов – очевидно, нетривиальная. Третьего исхода здесь не дано.

Очень важные выводы можно сделать, если рассмотреть линейную комбинацию, равную нулевому вектору

.

Дадим определение линейно- зависимой и линейно-независимой системы векторов, которое является в Линейной алгебре основным или, как говорят, фундаментальным понятием.

ОПРЕДЕЛЕНИЕ. Система векторов называется линейно- зависимой, если равная нулевому вектору линейная комбинация этих векторов

(2)

является нетривиальной, в противном случае возможна только тривиальная линейная комбинация, т.е когда все коэффициенты и система векторов, в этом случае, называется линейно-независимой.

Соотношение (2) является уравнением, в котором неизвестными величинами являются коэффициенты . Отметим, что уравнение (2) всегда имеет решение, так как очевидно, что одним из решений уравнения (2) является нулевое решение, когда все неизвестные коэффициенты равны нулю.

Отметим два очевидных свойства.

Свойство 1. Каждая подсистема линейно-независимой системы векторов является линейно-независимой.

Свойство 2. Если в систему векторов входит нулевой вектор, то она является линейно-зависимой.

Задание. Докажите свойство 1 и свойство 2.

Докажем основную теорему о линейной зависимости, аналогичную Теореме 4.

ТЕОРЕМА 6. Теорема о линейной зависимости. Для того, чтобы система векторов была линейно- зависимой, необходимо и достаточно, чтобы один из векторов линейно выражался через остальные (см. Теорему 4).

Доказательство. Необходимость.

Пусть система векторов является линейно-зависимой. Тогда нулевая линейная комбинация этих векторов

является нетривиальной, т.е. среди коэффициентов имеются, коэффициенты не равные нулю. Пусть , тогда при делении на мы получаем

.

Следовательно, вектор линейно выражается через остальные векторы системы, т.е. является линейной комбинацией остальных векторов.

Необходимость доказана.

Достаточность. Пусть вектор является линейной комбинацией остальных векторов

.

Перенесем вектор в правую часть уравнения

В результате мы получим нетривиальную линейную комбинацию, так как коэффициент при векторе равен . Следовательно, система векторов является линейно-зависимой.

Достаточность доказана.

Теорема доказана.

Базис и размерность линейного пространства.

При рассмотрении свойств линейного пространства возникает очевидный вопрос о существовании максимальной линейно-независимой системы векторов. Из геометрии мы знаем, что на плоскости существует не более 2 –х линейно-независимых векторов, причем любые три вектора линейно-зависимы. В 3-х мерном пространстве существует не более 3-х линейно-независимых векторов, причем любые 4-е вектора …..

Итак, рассмотрим вопрос о существовании максимального количества линейно-независимых векторов линейного пространства?

Пусть такая максимальная линейно-независимая система векторов существует (а она существует!, Не так ли). Эта система имеет особое значение и с ней связаны следующие основные понятия:

• базис линейного пространства;

• размерность линейного пространства;

• координаты вектора;

Эти понятия играют важнейшую роль в линейной алгебре.

Дадим определения.

ОПРЕДЕЛЕНИЕ. Система векторов называется базисом линейного пространства если она удовлетворяет двум условиям:

а) является линейно-независимой системой векторов;

б) каждый вектор является линейной комбинацией этой линейно- независимой системы векторов.

ОПРЕДЕЛЕНИЕ. Линейное пространство называется - мерным, если в нем существует базис из векторов, а число называется размерностью линейного пространства.

Для указания размерности пространства используется символическая запись:

,

( dimension = размерность).

В дальнейшем векторы базиса - мерного линейного пространства мы будем обозначать следующим образом:

- базис линейного пространства ,

или следующее обозначение: - базис линейного пространства .

Каждому вектору базиса мы присвоили порядковый номер. Следовательно, мы упорядочили векторы базиса. Это будет весьма полезно для дальнейшего.

По этому случаю приведем известное высказывание:

«Форма существенна. Сущность оформлена».

Согласно пункту б) ОПРЕДЕЛЕНИЯ базиса любой вектор линейного пространства, например, вектор , является некоторой линейной комбинацией базисных векторов:

(2)

Это выражение можно записать в компактной форме

(3)

Числа являются компонентами или координатами вектора , разложенного по базису.

Таким образом, мы приходим к следующему определению:

ОПРЕДЕЛЕНИЕ. Числа в соотношении называются координатами вектора в базисе .

Координаты вектора обычно записывают в виде строки:

,

либо в виде столбца

.

Таким образом, координаты вектора можно записать в виде матрицы из одной строки и - столбцов, либо - строк и одного столбца.

Эти записи равноправны. А именно, при транспонировании строки получается столбец и, наоборот, при транспонировании столбца получается строка.

Примеры базисов:

1. . Множество вещественных чисел является вещественным линейным пространством по отношении к обычным операциям сложения и умножения вещественных чисел.

Размерность этого пространства равна единице . Базис состоит из одного вектора (в данном случае вещественного числа). В качестве базисного вектора можно выбрать число один:

2. . Множество комплексных чисел является комплексным линейным пространством по отношению к обычным операциям сложения и умножения комплексных чисел. Размерность этого пространства . Базис состоит из двух векторов (в данном случае комплексных чисел). В качестве базисных векторов можно выбрать вещественное число 1 и мнимую единицу :

3. . Множество строк 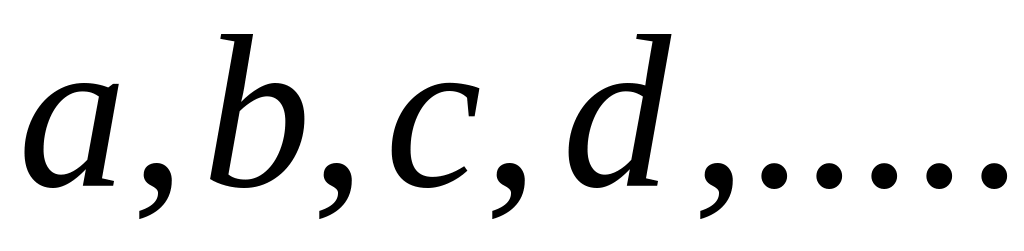длиной вида , где - вещественные числа, является вещественным линейным пространством. Это пространство известно, как - мерное координатное пространство. Размерность этого пространства . Базис состоит из векторов. В качестве базиса можно выбрать следующие строки:

……………………..

4. . Множество всех полиномов , степень которых не выше заданного натурального числа

. образует линейное пространство. Размерность этого пространства . Базис состоит из векторов. В качестве базисных векторов можно выбрать степени переменной :

……………………..

5. . Множество всех функций одной независимой переменной , определенных и непрерывных на отрезке , является линейным пространством. Размерность этого пространства . Базис состоит из бесконечного (счетного) количества векторов. В качестве базисных векторов можно выбрать степени переменной от нулевой степени до сколь угодно большой:

………..

……….

Примечание: Если в линейном пространстве могут существовать линейно- независимые системы векторов с любым количеством векторов, то в этом случае его размерность считается бесконечной.

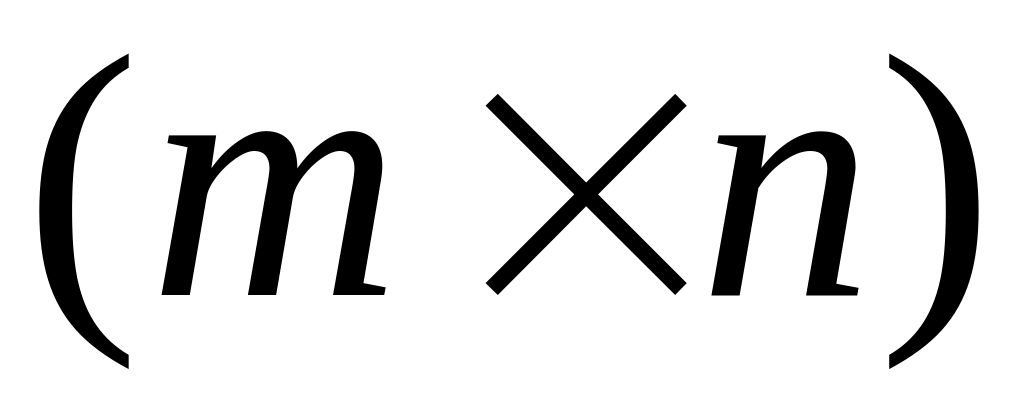6. . Множество матриц порядка является линейным пространством. Размерность этого пространства .

Рассмотрим линейное пространство квадратных матриц . Его размерность . В качестве четырех базисных векторов можно выбрать базис Вейля, состоящий из следующих матриц:

, , , .

ЛЕКЦИЯ 5

Теорема 7. О координатах вектора. Подпространство и линейная оболочка. Операции над линейными пространствами. Изоморфизм линейных пространств.

«Черепаху догонит только тот Ахилл, который ее уже догнал»

ТЕОРЕМА 7. Теорема о координатах вектора. В данном базисе координаты вектора определены однозначно.

Доказательство. Доказательство теоремы выполним «от обратного».

Предположим, что в базисе вектор обладает двумя наборами координат: первый набор координат , второй набор координат . Следовательно, имеем два разложения

(а)

(б)

Вычитаем (б) из (а)

.

Так как базис является линейно-независимой системой векторов, то их нулевая линейная комбинация является тривиальной, т.е.

Следовательно, наборы координат совпадают: , .

Теорема доказана.

Подпространство и линейная оболочка. Операции над линейными пространствами.

Рассмотрим множество и в нем некоторое его подмножество , .

Пусть множество является линейным пространством.

Рассмотрим вопрос при каких условиях множество образует линейное подпространство в пространстве ?

ОПРЕДЕЛЕНИЕ. Подмножество является линейным подпространством в пространстве , если выполнены два условия:

1. ;

2. ;

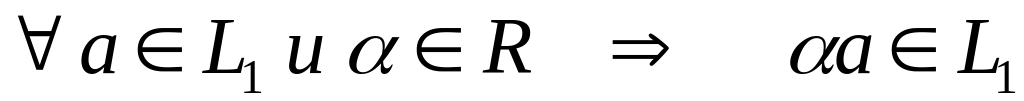Выполнение этих двух условий означает, что при сложении векторов из множества (первое условие) и умножения вектора на число (второе условие) получается вектор, который принадлежит подмножеству . Тогда подмножество будет подпространством.

Рассмотрим некоторую систему векторов .

ОПРЕДЕЛЕНИЕ. Линейной оболочкой системы векторов называется множество всевозможных линейных комбинаций этих векторов:

Введем обозначение линейной оболочки :

=

Всякая линейная оболочка является подпространством в .

Рассмотрим вопрос о размерности линейной оболочки.

Размерность линейной оболочки равна рангу матрицы , строки которой составлены из векторов (координат) данной системы векторов :

.

Пример. Рассмотрим систему из 5-ти векторов: , , , , . Найдем размерность линейной оболочки системы векторов Для этого рассмотрим матрицу, составленную из координат данных векторов, и найдем ее ранг:

,

Базисным минором матрицы является, например минор , в который входят первая, вторая и пятая строки. Это означает, что векторы образуют линейно-независимую систему векторов.

Следовательно,

Ответ: размерность линейной оболочки равна 3.

Операции над линейными пространствами.

Рассмотрим два (можно и более) линейных пространства и . Объединение и пересечение этих пространств является также линейным пространством: объединение и пересечение являются линейными пространствами. Поставим вопрос о том, чему равна размерность объединения ?

Из комбинаторики известна формула нахождения числа элементов при объединении конечных множеств. Пусть и конечные множества, - число элементов в множестве ,

- число элементов в множестве .

Тогда, число элементов в объединении этих множеств

.

Эта формула выполняется при подсчете размерности объединения двух линейных пространств .

ТЕОРЕМА 8. Пусть и линейные пространства. Тогда

Доказательство.

Выберем в пересечении базис, состоящий из векторов

, следовательно . Тогда в линейных пространствах и можно выбрать следующие базисы:

пусть - базис в , ,

- базис в , .

Тогда, система векторов

,

Является линейно-независимой системой векторов и образует базис в .

Следовательно

Теорема доказана.

Кроме операции объединения линейных пространств рассматривают, также операцию взятия прямой суммы линейных пространств:

.

Знак обозначает прямую сумму пространств. Как правило, пространства и считаются подпространствами некоторого линейного пространства . Вопрос. Какой смысл несет в себе операция прямой суммы? Смысл этой операции раскрывает следующее ОПРЕДЕЛЕНИЕ и ТЕОРЕМА 9.

ОПРЕДЕЛЕНИЕ. Линейное пространство является прямой суммой линейных пространств и , обозначение , если каждый вектор можно представить единственным образом в виде

, причем , , и

Используя определение прямой суммы линейных пространств, поставим задачу о разложении линейного пространства в прямую сумму его подпространств и . Докажем следующую теорему.

ТЕОРЕМА 9. Для того чтобы достаточно, чтобы, пересечение .

Доказательство.

Пусть - базис подпространства , а

- базис подпространства .

Докажем, что система векторов , образует базис пространства . Для этого достаточно доказать линейную независимость этой системы векторов. Рассмотрим нулевую линейную комбинацию этой системы

.

Выполним преобразование

.

Слева вектор, принадлежащий , справа вектор, принадлежащий , причем пересечение содержит только нулевой вектор, т.е.

а это означает (!), что все коэффициенты и . В результате система векторов , линейно-независимая. Следовательно, для каждого вектора выполняется разложение

,

причем , где

Полученное разложение вектора на сумму векторов и т.е. единственно.

Изоморфизм линейных пространств.

Тезис: линейные пространства одинаковой размерности неотличимы.

Обоснование тезиса. А собственно говоря, чем одно линейное пространство отличается от другого? Между собой пространства отличаются только размерностями. Вспомним определение линейного пространства: множество элементов произвольной природы … и т.д.

Пример. Рассмотрим два линейных пространства.

1. Линейное пространство множество, векторов вида ,

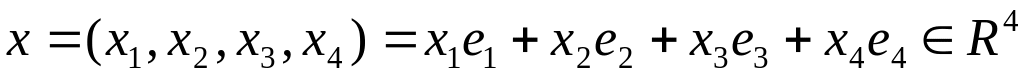где базисные векторы , , , .

2. Линейное пространство - множество матриц порядка 2х2 вида

где базисные векторы

, , , .

представляют собой базис Вейля.

В этих примерах конкретный вид базисных векторов не существен.

Сформулируем определение.

ОПРЕДЕЛЕНИЕ. Линейные пространства и , называются изоморфными, если между векторами этих пространств можно установить взаимно-однозначное соответствие, при котором выполняются следующие два условия:

Если векторы соответствуют векторам , т.е. если

и то

1. ,

2. .

Здесь знак обозначает взаимно-однозначное соответствие векторов.

Дадим эквивалентное определение.

ОПРЕДЕЛЕНИЕ. Изоморфизм линейных пространств это линейное отображение одного пространства в другое пространство (взаимно-однозначное линейное отображение).

Пусть , где - отображение. Пусть

и

Тогда

,

ТЕОРЕМА 10. Теорема об изоморфизме. Линейные пространства одинаковой размерности являются изоморфными.

Доказательство.

Рассмотрим два линейных пространства и , одинаковой размерности

и пусть - базис в

- базис в

Рассмотрим в некоторый вектор

В выберем вектор , у которого такие же координаты, что и у вектора (такой выбор всегда можно сделать) и установим между этими векторами соответствие

.

В силу теоремы 7 о единственности разложения вектора по базису соответствие , установленное между векторами и является взаимно-однозначным. Следовательно, линейные пространства и изоморфны.

Теорема доказана.

ЛЕКЦИЯ 6

Преобразование вектора при преобразовании базиса. Системы линейных уравнений. Теорема Кронекера-Капелли. Формула Крамера. Фундаментальная система решений.

«…мышление строится таким образом, что даже если начала кажутся неверными, то следствия и выводы, полученные на основе этих начал будут всегда истинными» Р.Декарт, «Начала философии»

Преобразование вектора при преобразовании базиса

Рассмотрим линейное пространство и пусть .

Выберем в два базиса:

базис , назовем его старым базисом;

базис , назовем этот базис новым;

Выполним разложение базисных векторов старого базиса по векторам нового базиса

(1)

……………………………………………………….

Запишем эти равенства в матричной форме:

; , (1а)

где столбцы и .

Соотношения (1) и (1а) определяют матрицу , которая называется матрицей преобразования базисов, или матрицей перехода от старого базиса к новому базису . Так как система векторов линейно-независима (составляет базис), то столбцы матрицы также линейно-независимы, следовательно и . Поэтому существует обратная матрица .

Разложим некоторый вектор по старому и новому базису:

(2)

(2а)

где - координаты вектора в старом базисе, - координаты вектора в новом базисе. Выполним преобразование, а именно, подставим (1а) в (2а)

Отсюда следует , или , или

…………………………………………

В итоге - это формулы преобразования базисов и координат.

Замечание. Обратите внимание, что если в матричных соотношениях матрица стоит левее вектора, то вектор записывается в виде столбца, а если правее, то в виде строки.

На этом мы заканчиваем рассмотрение линейного пространства и переходим к рассмотрению систем линейных уравнений.

Системы линейных уравнений

Рассмотрим систему из - уравнений, содержащую - неизвестных

Введем основную матрицу и расширенную матрицу ,

,

а также, столбец неизвестных и столбец правой части уравнения

, .

Матричный вид записи системы линейных уравнений:

.

Классификация системы линейных уравнений:

- неоднородная система уравнений, если .

- однородная система уравнений, если .

Классификация решений:

• Система уравнений называется совместной, если имеет решение.

• Система уравнений несовместна, если не имеет решений.

ТЕОРЕМА 11. Теорема Кронекера-Капелли.

Для того, чтобы система уравнений была совместной (имела решение) необходимо и достаточно, чтобы совпадали ранги основной и расширенной матриц: .

Необходимость. Пусть система совместна и имеет решения

Рассмотрим столбцы матрицы и пусть . По теореме о базисном миноре базисные столбцы линейно-независимые, а все остальные столбцы этой матрицы являются линейными комбинациями ее базисных столбцов. Так как система уравнений совместна, то столбец является линейной комбинацией столбцов матрицы (и ее базисных столбцов):

,

где - столбцы матрицы . Следовательно, .

Достаточность. Пусть ранги основной и расширенной матриц совпадают

.

Докажем, что тогда система уравнений будет совместной. Так как ранги совпадают, то очевидно, что базисных столбцов матрицы будут являться базисными и для матрицы . Следовательно, столбец не может входить в число базисных столбцов и, согласно теореме о базисном миноре, будет некоторой линейной комбинацией базисных столбцов матрицы . Это означает, что существуют некоторые числа , такие что

.

В результате мы получили систему уравнений , в котором набор чисел является решением этой системы уравнений.

Теорема доказана.

Формула Крамера.

Рассмотрим квадратную систему уравнений: - уравнений с - неизвестными

Пусть . Тогда и система уравнений совместна. Кроме того, у матрицы существует обратная матрица. Решая матричное уравнение : , получаем

.

Это и есть формула Крамера в матричном виде. Формулу Крамера часто записывают в следующем виде

, где , а - определитель матрицы , в которой столбец заменен на столбец .

Фундаментальная система решений.

Рассмотрим однородную систему уравнений: . На основании выше сказанного сделаем три утверждения

1. Однородная система уравнений всегда совместна. Так как столбец , то .

2. У однородной системы уравнений всегда существует нулевое решение , т.к. 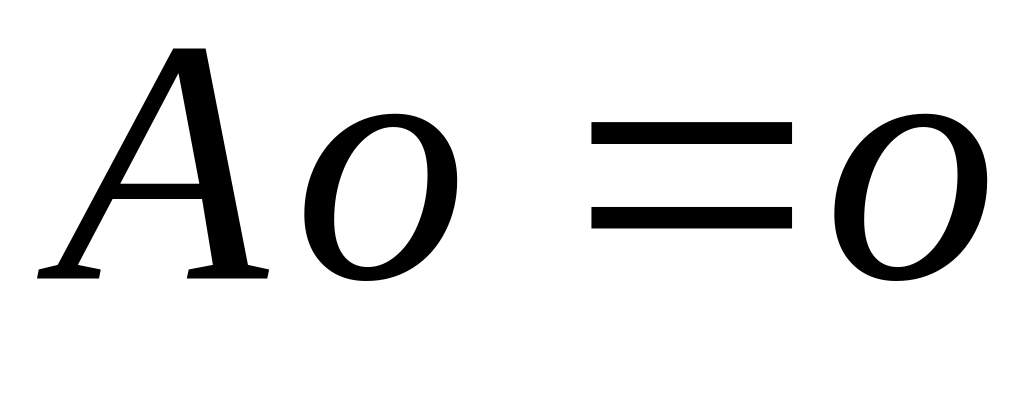. Нулевое решение называется тривиальным решением.

3. Основная задача – найти условия, при которых однородная система уравнений будет иметь нетривиальное решение (ненулевое решение).

Столбец , составленный из неизвестных

мы вправе рассматривать, как вектор -мерного линейного пространства. В этом случае систему уравнений можно интерпретировать следующим образом: матрица преобразует вектор в нулевой вектор .

ТЕОРЕМА 12. Теорема о существовании нетривиального решения. Однородная система - уравнений с - неизвестными имеет нетривиальное решение тогда и только тогда, когда ранг матрицы меньше , .

Доказательство. Рассмотрим однородную систему уравнений

Запишем систему уравнений в виде линейной комбинации столбцов матрицы :

Если среди чисел найдутся ненулевые, то столбцы будут линейно-зависимыми (вспомним определение линейной зависимости системы векторов). Тогда, в силу теоремы о базисном миноре . Из столбцов матрицы, только столбцов являются базисными. В результате мы получили условие существования нетривиального решения и доказали теорему.

Теорема доказана.

Следствие. Для квадратной системы уравнений нетривиальное решение будет при условии, что Это условие эквивалентно условию .

Найдем нетривиальное решение однородной системы уравнений

.

Число неизвестных в системе уравнений равно (число столбцов матрицы).

Пусть , причем меньше и система уравнений, согласно Теореме 12, имеет нетривиальное решение. Столбцы матрицы линейно-зависимы. Пусть базисный минор матрицы расположен в правом верхнем углу, т.е. первые столбцов являются базисными.

По теореме о линейной зависимости, один из столбцов линейно выражается через остальные, а значит и через базисные столбцы (см. теорему о базисном миноре). Преобразуем систему уравнений, оставив в левой части уравнения базисные столбцы и перенеся остальные на право

Систему уравнений запишем в матричном виде , где матрица

является квадратной порядка , причем . Далее используем формулу Крамера и получаем решения.

где - произвольные.

Выберем следующие значения произвольных

, комбинаций.

Примечание. Такой выбор произвольных, нули и единицы, является простейшим из возможных.

В результате мы получим частных решений , которые запишем в виде строк

Эти частные решения системы уравнений представляют собой линейно-независимую систему векторов линейного пространства.

Мы вынуждены сформулировать следующие важные определения.

ОПРЕДЕЛЕНИЕ. Полная система частных линейно-независимых решений называется фундаментальной системой решений соответствующей однородной системы уравнений.

ОПРЕДЕЛЕНИЕ. Общим решением однородной системы уравнений называется всякая линейная комбинация векторов фундаментальной системы решений

Общее решение записано, как линейная оболочка частных решений, или векторов.

Так как частные решения - линейно-независимы, то они образуют базис пространства решений. В результате решение однородной системы уравнений проводит нас к понятию пространства решений однородной системы уравнений.

Пояснение. Мы рассматриваем однородную систему - уравнений с - неизвестными . Столбец , составленный из неизвестных , мы интерпретируем, как вектор некоторого линейного пространства размерности . В правой части уравнения находится нулевой столбец, составленный из нулей.

ЛЕКЦИЯ 7

Скалярное произведение и евклидово пространство. Примеры задания скалярного произведения. Неравенство Коши-Буняковского. Нормированное пространство. Ортогональность. Ортогональный базис и его свойства. Матрица Грама.

«…поле наблюдения предметов, явлений, событий однородно и непрерывно в том смысле, что я могу переносить себя в любую точку в качестве носителя наблюдаемых событий и явлений – в этом суть классического идеала рациональности» М.К.Мамардашвили

Скалярное произведение и евклидово пространство.

Линейное пространство мы определили как множество, в котором заданы две операции:

- сложение векторов;

- умножение вектора на число.

Однако в геометрии и в алгебре вводятся такие понятия как:

• длина вектора;

• угол между векторами;

• скалярное произведение;

• и др.

Из этих понятий основным выбирают понятие скалярного произведения, см. ниже Замечание 2.

Замечание 1.

Понятия, утверждения и теоремы геометрии и линейной алгебры удобно иллюстрировать чертежами и рисунками. Однако, в алгебре это опасно и не всегда возможно, так как связано:

а) c малой размерностью (трех мерностью) пространства, в котором мы живем;

б) c необходимостью рассматривать комплексные числа;

в) c евклидовой структурой физического пространства (квантовая физика).

Кроме того, чертежи и рисунки несут принудительную информацию о метрических свойствах пространства – о длине, углах и т.п.

Замечание 2.

В геометрии на плоскости и в пространстве важную роль играют метрические понятия, связанные с измерением, такие как длина вектора и угол между векторами. Длина вектора не является линейной функцией от вектора (координат вектора), угол между двумя векторами не является линейной функцией от одного из векторов при фиксированном втором.

Несмотря на это, из длин двух векторов и угла между ними при помощи действий, далеких от линейности, можно построить скалярное произведение:

,

причем скалярное произведение является билинейной функцией от векторов, т.е. линейной по вектору при фиксированном и линейной по вектору при фиксированном :

.

Тем самым скалярное произведение векторов с точки зрения алгебры проще длины вектора и угла между векторами. В свою очередь, эти величины весьма просто выражаются через скалярное произведение.

Все сказанное выше дает нам основания при введении метрических понятий в теорию многомерных линейных пространств выбрать скалярное произведение за основное понятие алгебры.

Дадим определение.

ОПРЕДЕЛЕНИЕ. В линейном пространстве задано скалярное произведение, если каждой паре векторов и поставлено в соответствие некоторое число, обозначаемое и удовлетворяющее следующим четырем аксиомам:

для вещественного линейного пространства – вещественное число

для комплексного линейного пространства - комплексное число

а к с и о м ы : а к с и о м ы :

1. 2. 3. 4. Причем при

1. 2. 3. 4. Причем при

ОПРЕДЕЛЕНИЕ. Линейное пространство, в котором задано скалярное произведение, называется евклидовым пространством, вещественным и/или комплексным.

ОПРЕДЕЛЕНИЕ. Комплексное евклидово пространство называется, также, унитарным.

Примеры задания скалярного произведения.

1 , 3 - мерное вещественное евклидово пространство.

Рассмотрим два вектора и .

Определим правило задания скалярного произведения следующей формулой

Легко проверить, что все 4 аксиомы выполняются.

2 , мерное вещественное евклидово пространство.

А) Простейший случай в . Рассмотрим два вектора и

и .

Определим скалярное произведение следующей формулой

Б) Общий вид задания скалярного произведения в для векторов и

,

где - числовые коэффициенты, из которых можно составить матрицу

.

Матрица называется метрическим тензором. Матрица , задающая скалярное произведение, должна удовлетворять первой и четвертой аксиомам:

Первая аксиома. Согласно первой аксиоме , то имеем следующие соотношения

,

, ( )

Следовательно, , т.е. - матрица симметричная.

Четвертая аксиома. Согласно четвертой аксиоме , тогда

Следовательно, матрица должна определять положительно-определенную квадратичную форму (квадратичные формы мы изучим позднее).

3 , мерное комплексное евклидово пространство (или унитарное пространство). .

Рассмотрим два вектора

,

Координаты этих векторов комплексные числа. Общий вид задания скалярного произведения

Черта над координатами вектора означает комплексное сопряжение.

Матрица , задающая скалярное произведение, должна удовлетворять двум условиям (первой и четвертой аксиомам унитарного пространства):

- Первое условие. Согласно первой аксиоме , имеем следующие соотношения

,

, ( )

Следовательно, , т.е. - матрица эрмитова.

- Второе условие. Так как, согласно четвертой аксиоме , то

Следовательно, матрица должна определять положительно-определенную полуторалинейную форму.

4 , где множество функций, определенных на отрезке .

, т.е. пространство бесконечномерное.

Рассмотрим две функции и , . Определим скалярное произведение функций и , используя определенный интеграл

.

Это простейший случай задания скалярного произведения в .

В общем случае скалярное произведение имеет вид

, где функция положительна на отрезке . Эта функция называется функцией распределения, или весовой функцией. Все аксиомы выполнены. Проверьте!

Неравенство Коши –Буняковского : .

Докажем неравенство для случая вещественного линейного пространства.

Рассмотрим векторы и , а также их линейную комбинацию , . Имеем

Это неравенство принимает лишь неотрицательные значения при любом . Следовательно, дискриминант не может быть положительным:

. Что и требовалось доказать.

Следствие. Из неравенства Коши – Буняковского следует неравенство

.

Извлечем из этого выражения квадратный корень и получим

, где - длина вектора .

Введем , где угол между векторами. Это можно сделать, так как выполняется очевидное условие.

.

Понятие длины вектора хорошо известно из геометрии. Оно ведет к следующему, очень важному понятию нормированного пространства, основанному на длине вектора.

ОПРЕДЕЛЕНИЕ. Линейное пространство, в котором введена длина или норма вектора , называется нормированным пространством, если выполнены три условия на норму вектора:

1. 

2. - неравенство треугольника.

3. 

Примечание: Условимся далее считать, что понятия норма вектора и длина вектора это одно и то же.

Любое евклидово пространство всегда является нормированным пространством, так как норму вектора всегда можно определить, используя скалярное произведение: квадратный корень из скалярного произведенияравен норме вектора, . При этом все три условия, входящие в ОПРЕДЕЛЕНИЕ нормированного пространства (на норму вектора), выполняются.

Используя норму вектора и угол между векторами, запишем скалярное произведение

.

Эта формула хорошо известна из курса геометрии.

Задача. Докажите неравенство треугольника, используя неравенство Коши-Буняковского.

Ортогональность. Ортогональный базис и его свойства. Матрица Грама.

Познакомимся с условием ортогональности двух ненулевых векторов.

ОПРЕДЕЛЕНИЕ. Векторы и называются ортогональными, если их скалярное произведение равно нулю,

.

Итак, если векторы ортогональны , то . И наоборот, если , то .

Из формулы следует, что . Таким образом, условие ортогональности двух векторов эквивалентно условию перпендикулярности этих векторов, хорошо известному в геометрии.

Рассмотрим следующее утверждение. В евклидовом пространстве существуют базисы, называемые ортогональными базисами, которые наиболее удобны и выбор которых значительно упрощает многие вычисления и доказательства.

Рассмотрим определение ортогонального базиса и докажем основную теорему.

ОПРЕДЕЛЕНИЕ. Базис линейного пространства называется ортогональным базисом, если выполняется следующее условие

(А)

Это условие означает, что базисные векторы взаимно ортогональны, т.е. при , а их длины равны единице, при , или .

Следовательно, ортогональный базис составлен из ортонормированных векторов, т.е. векторов единичной длины. Поэтому ортогональный базис и ортонормированный базис означают одно и то же.

ТЕОРЕМА 13. Система векторов , удовлетворяющая условию ортогональности (см. А), , является линейно-независимой системой и, следовательно, образует базис некоторого пространства.

Доказательство. Докажем линейную независимость системы векторов , удовлетворяющих условию . Для этого рассмотрим нулевую линейную комбинацию:

(Б)

Умножим эту комбинацию скалярно на вектор , затем на вектор и т.д.:

………………………………………………………………

Учтем условие ортогональности и получим:

…………

Следовательно, линейная комбинация (Б) является тривиальной, а система векторов линейно-независимой.

Теорема доказана.

Итак, согласно Теореме 13., всякая ортогональная система векторов является линейно-независимой и образует базис некоторого пространства.