
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Иркутский государственный университет»
Карнаков В.А.
Лекции по линейной алгебре
Учебное пособие
г. Иркутск
2013г.
ПРЕДИСЛОВИЕ
Настоящее учебное пособие адресовано студентам университетов, обучающихся по физическим направлениям бакалавриата. При работе над пособием автор стремился максимально сохранить стиль и дух устного изложения линейной алгебры, используя для этого собственный конспект лекций.
Устная речь с точки зрения грамматики русского языка содержит подчас «неправильности», которые делают ее более выразительной и наглядной. При «переводе» устной речи на письменный язык невольно исправляются огрехи устной речи, делаются дополнения и уточнения, которые необходимы для достижения полноты изложения предмета лекции. Поэтому текст учебного пособия приобретает черты академического изложения.
Теперь скажем несколько слов о содержании линейной алгебры. Д.К.Фаддеев в «Лекциях по алгебре» отмечает, что «Исследование линейных пространств составляет содержание линейной алгебры». Теперь о предмете. Во-первых, линейная алгебра, наряду с математическим анализом вещественной и комплексной переменной, составляет фундамент математического образования, без которого невозможно изучение и понимание современных теорий классической и квантовой физики. Во-вторых, трудно переоценить значение линейной алгебры в физическом образовании.
Стиль лекций по математике очень важен для понимания ее студентами и колеблется от наивного, подчас популярного, изложения для студентов младших курсов, до сверхсложного профессионального уровня для студентов старших курсов. Тот и другой подходы – крайности. Найти золотую середину крайне важно при преподавании математики. Как пример: трудности изучения линейной алгебры связаны, обычно, с использованием аксиоматического метода, положенного в основу традиционного изложения алгебры. Еще одной особенностью линейной алгебры является универсальность алгебраических понятий (пространство, вектор, отображение, линейная форма и т.д.), которая формирует определенные связи между различными разделами математики.
Каждая лекция сопровождается эпиграфом с целью, а иногда и без, отразить смысловое содержание лекции. Из всех эпиграфов наиболее интересными являются высказывание писателя М.Булгакова – «Будите свою фантазию, пришпоривайте ее» и философа М.К.Мамардашвили «Понятие числа предполагает понятие множества и порядка. Поэтому человек, конечное существо, постигая мир, приобщается к бесконечно полной информации»
Очень важно пробудить у слушателя математическую фантазию, как способ рассуждений, помогающий понять математические теории. Итак, впереди нас ждет интересный путь протяженностью в один семестр под названием «Линейная алгебра».
ЛЕКЦИЯ 1
Программа. Учебная литература. Что изучает алгебра? Линейность. Функция. Матрицы и операции над матрицами.
Программа курса Линейная алгебра
Матрицы и определители;
Линейное пространство;
Системы линейных уравнений;
Евклидовы пространства;
Линейные операторы;
Билинейные и квадратичные формы
Функции от матриц;
-
“Понятие числа предполагает понятие множества и порядка. Поэтому человек, конечное существо, постигая мир, приобщается к бесконечно полной информации”
М.К.Мамардашвили
Учебная литература
Ильин В.А., Позняк Э.Г.: - “Линейная алгебра”
Федорчук В.В.: - “Курс аналитической геометрии и линейной алгебры”
Канатников А.Н., Крищенко А.П.: - Линейная алгебра, 1998г. Изд. МВТУ им. Баумана
Ефимов Н.В., Розендорн Э.Р.: - Линейная алгебра и многомерная геометрия
Гельфанд И.М.: - “Лекции по линейной алгебре”
Александров П.С.: - “Курс аналитической геометрии и высшей алгебры”
Курош А.Г.: - “Курс высшей алгебры”
Шилов Г.Е.: - “Конечномерные линейные пространства”
Бугров, Никольский: - Элементы линейной алгебры и аналитической геометрии
Беклемишев Д.В.: - “Курс аналитической геометрии и высшей алгебры”
Кострикин А.И., Манин Ю.М.: - “Линейная алгебра”. Изд. МГУ
Гантмахер Ф.Э.: - “Теория матриц”
Фаддеев Д.К. : -”Лекции по алгебре”, 2005г.
Сборники задач
Проскуряков М.В.: - Сборник задач по линейной алгебре
Фаддеев Д.К., Соминский И.С.: - Задачи по высшей алгебре
Примечание: жирным шрифтом выделены основные учебники.
Что изучает алгебра! Линейность. Функция.
Множества, изучаемые в математике.
-
Числовые множества:
 - Натуральные
числа
- Натуральные
числа - Целые числа
- Целые числа - Рациональные
числа
- Рациональные
числа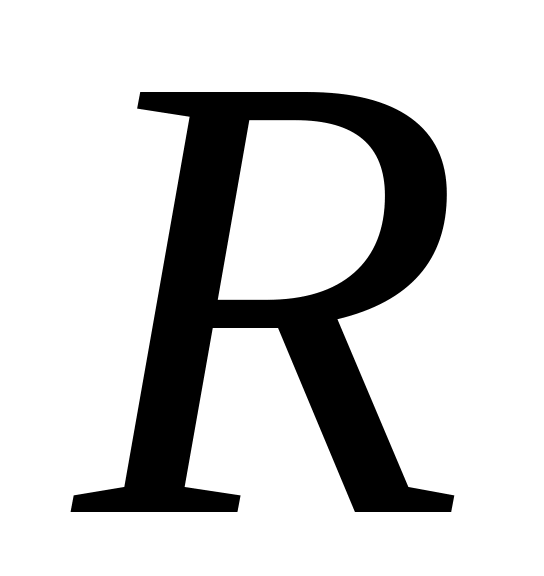 - Вещественные
числа
- Вещественные
числа- Комплексные числа:
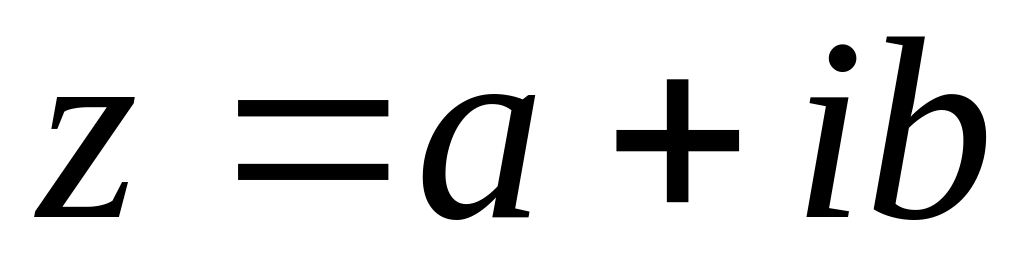
- Кватернионы:

где

Октавы: …………
Другие множества:
Функции:
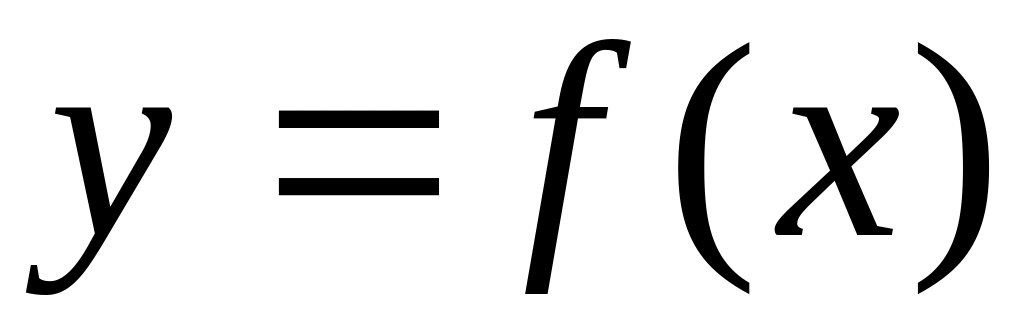
Векторы:

 ….
….Матрицы:
 ,…
,…
Операторы:
 ,…
,…Тензоры:

 ….
….Спиноры:
 ….
….
О предмете математика.
«Когда на вопрос, что изучает математика, отвечают: множества с заданными в них отношениями, то это вряд ли можно признать ответом. Ведь среди континуума мыслимых множеств с заданными в них отношениями, или структур, математиков реально привлекает редкое, дискретное множество. И смысл вопроса заключается в том, чтобы понять, чем же особенно ценна эта исчезающе малая часть, вкрапленная в аморфную массу.
… Точно также, смысл любого математического понятия лишь в малой степени содержится в его формальном определении. Не меньше, скорее больше, дает набор основных примеров, являющихся, одновременно, и мотивировкой, и содержательным определением и смыслом понятия».
И.Р.Шафаревич, академик РАН
Линейная алгебра базируется на аксиоматическом методе, согласно которому вводятся первичные, неопределяемые понятия, подчиняющиеся некоторому набору аксиом. В элементарной геометрии первичными понятиями являются точка, прямая и плоскость, а аксиомами являются, например, следующие утверждения:
- каковы бы ни были две точки А и В, существует прямая, которой принадлежат две эти точки (т.е. через две точки проходит прямая, и притом только одна);
- в плоскости, определяемой точкой А и прямой L существует не более одной прямой, проходящей через А и не пересекающей L (т.е. через одну точку можно провести единственную прямую, параллельную данной).
Аксиомы – это первичные утверждения, которые считаются верными изначально. Аксиоматический метод позволяет все утверждения теории выводить из заданных аксиом. Доказательства утверждений проводятся более строго, но и более формально. В результате линейная алгебра, в отличие от геометрии, становится менее наглядной и более сложной для восприятия. Однако трудности изучения линейной алгебры окупаются возможностью увидеть и установить связи между различными разделами математики. Это приводит к фундаментальным понятиям математики и формирует единство ее логических принципов.
Линейность. В физике основные принципы и законы выражаются на языке математики в виде линейных конструкций. Почти всякий естественный процесс, и физический в том числе, почти всюду, в малом, линеен. С более общей точки зрения, содержание линейной алгебры состоит в разработке математического языка для выражения одной из самых простых и, одновременно, общих естественнонаучных идей – идеи линейности.
Например, эффективность применения дифференциального исчисления для описания физических и механических явлений связана с тем, что малые приращения некоторых двух физических величин между собой пропорциональны:
![]() ,
,
где
![]() и
и
![]() физические величины,
физические величины,
![]() и
и
![]() приращения физических величин,
приращения физических величин,![]() коэффициент пропорциональности
(производная).
коэффициент пропорциональности
(производная).
Квантовая физика XX века резко расширила сферу применения идеи линейности, добавив к принципу линейности малых приращений принцип суперпозиции векторов состояний. В результате линейная алгебра превратилась в аппарат, используемый для формулировки фундаментальных физических законов природы, например, объясняющих таблицу Менделеева, систематику элементарных частиц и даже свойства пространства-времени.
Однако, все сложнее. Окружающий нас мир природы не всегда допускает линейные способы и модели описания явлений. Типичным примером нелинейного явления является солитон. Мир полон как линейными, так и нелинейными явлениями.
Мир не линеен и поэтому сложен.
Функция. Когда мы говорим о функции, всегда подразумеваем следующую запись:
![]() ,
где
,
где
![]()
Функция – это
отображение одного множества
![]() в
другое множество
в
другое множество
![]() .
Следовательно, чтобы задать функцию
необходимо задать отображение.
.
Следовательно, чтобы задать функцию
необходимо задать отображение.
ОПРЕДЕЛЕНИЕ:
Если для каждого элемента
,
принадлежащего множеству
![]() ,
поставлен в соответствие некоторый
элемент
,
поставлен в соответствие некоторый
элемент![]() ,
принадлежащий множеству
,
принадлежащий множеству
![]() ,
то говорят, что на множестве
задана некоторая функция
со
значениями на множестве
.
,
то говорят, что на множестве
задана некоторая функция
со
значениями на множестве
.
Итак, функция![]() задана,
если множество
отображается
в множество
посредством функции
.
Символически это записывается так
задана,
если множество
отображается
в множество
посредством функции
.
Символически это записывается так
![]() .
.
Или,
![]()
![]()
![]() ,
то существует
,
то существует
![]() .
.
 Функция
Функция



В математике исторически сложились следующие синонимы понятия функция: |
|
Немного истории.
Греция, 3 век до р.х. Легенда.
Вызвал к себе царь Евклида, написавшего 15 книг по математике и говорит:
“Слушай, разве подобает мне, царю, изучать все эти 15 книг. Как царь, я должен знать геометрию, но твой путь очень длинен для меня. Я повелеваю тебе указать в изучении геометрии Царский путь, более короткий для меня”.
Евклид ответил: “К сожалению, в науке нет царских путей. Как все смертные,
ты царь, если хочешь постичь геометрию, должен пройти
весь длинный путь, указанный мной в «Началах геометрии»”.
Лекции, семинары, изучение теории, решение задач и самостоятельная работа – вот путь студента в университете.
Матрицы и операции над матрицами.
ОПРЕДЕЛЕНИЕ:
Прямоугольная
таблица чисел
![]() ,
состоящая из
,
состоящая из
![]() -
строк и
-
строк и
![]() - столбцов, называется матрицей порядка
- столбцов, называется матрицей порядка
![]() .
.
Запись матрицы
![]() ,
у которой
- строк и
– столбцов с элементами
,
у которой
- строк и
– столбцов с элементами
![]() :
:
![]()
![]() - элемент матрицы,
это вещественное или комплексное число:
- элемент матрицы,
это вещественное или комплексное число:
![]() .
.
Матрицей
порядка
![]() является строка
является строка
![]()
Матрицей
порядка
![]() является столбец
является столбец
![]()
В дальнейшем,
как правило, мы будем иметь дело с
матрицами порядка
![]() ,
т.е. квадратными матрицами
-го
порядка, у
которых количество строк совпадает с
количеством столбцов.
,
т.е. квадратными матрицами
-го
порядка, у
которых количество строк совпадает с
количеством столбцов.
Примеры простейших матриц:
нулевая
матрица
![]() ,
единичная матрица
,
единичная матрица
![]() ,
диагональная, треугольная, блочная
матрицы и т.д.
,
диагональная, треугольная, блочная
матрицы и т.д.
Задание. Запишите примеры этих матриц.
Вопрос. Какие действия можно производить над матрицами? При этом крайне важны свойства, которыми обладают операции над матрицами.
При введении операций сложения матриц, умножения матрицы на число, произведения матриц исходят из следующего основного требования – результат сложения и произведения матриц должен оставаться матрицей. При этом необходимо учитывать, что не всякие матрицы можно сложить и перемножить между собой, т.е. имеются ряд ограничений. Например, сложение матриц определено для матриц одинакового порядка, произведение двух матриц определено для случая, когда количество столбцов первой матрицы равно количеству строк второй матрицы. В линейной алгебре, кроме обычных операций сложения матриц, произведения матриц, произведения матрицы на число, вводятся и другие очень важные операции:
транспонирование;
прямая сумма;
след матрицы;
определитель матрицы;
нахождение обратной матрицы;
эрмитово сопряжение и др.
Операции над матрицами.
Сложение матриц одинакового порядка
 :
:
![]() ,
где
,
где
![]()
Свойства операции сложения:

Умножение матрицы на число:
![]() ,
где
,
где
![]()
Свойства операции умножения:

Произведение матриц и
 ,
,

![]() ,
где элементы
,
где элементы
![]() матрицы
матрицы
![]() :
:
![]()
Правило произведения
«читается» следующим образом: элемент
![]() равен сумме
произведений элементов
равен сумме
произведений элементов
![]()
![]() ой
строки первой
матрицы и элементов
ой
строки первой
матрицы и элементов
![]()
![]() го
столбца второй матрицы.
го
столбца второй матрицы.
Очевидно, что
произведение матриц не всегда коммутативно,
т.е.
![]() (обязательно проверьте это). Если
окажется, что
(обязательно проверьте это). Если
окажется, что
![]() ,
то говорят, что матрицы
и
,
то говорят, что матрицы
и
![]() коммутативны.
коммутативны.
Произведение матриц всегда ассоциативно и дистрибутивно, т.е. выполняются следующие свойства:

Для квадратных матриц, и это очень важно, можно определить такие операции, как произведение Ли и произведение Иордана:
![]() - произведение
Ли, или
коммутатор.
- произведение
Ли, или
коммутатор.
![]() - произведение
Иордана, или
антикоммутатор.
- произведение
Иордана, или
антикоммутатор.
Как мы видим, эти операции вводятся на базе обычного произведения матриц.
Транспонирование.
Рассмотрим матрицу
.
Выполним над строками матрицы
операцию
транспонирования,
а именно строки матрицы
запишем столбами некоторой матрицы
![]() ,
которую назовем транспонированной,
по отношению к матрице
:
,
которую назовем транспонированной,
по отношению к матрице
:
![]() ,
,
![]() .
.
Символ
![]() ,
стоящий справа над матрицей, указывает
на то, что над этой матрицей выполнена
операция
транспонирования,
или просто – транспонирование.
Транспонирование
можно применять к матрицам любого
порядка.
,
стоящий справа над матрицей, указывает
на то, что над этой матрицей выполнена
операция
транспонирования,
или просто – транспонирование.
Транспонирование
можно применять к матрицам любого
порядка.
Свойства операции транспонирования:

Для квадратных
матриц можно установить выполнение
ряда свойств. Пусть матрица и ее
транспонированная
совпадают,
![]() .
Такая матрица называется симметричной.
Элементы симметричной матрицы,
расположенные симметрично относительно
главной диагонали, равны между собой
т.е.
.
Такая матрица называется симметричной.
Элементы симметричной матрицы,
расположенные симметрично относительно
главной диагонали, равны между собой
т.е.
![]() .
.
Если матрица
противоположна ее транспонированной,
![]() ,
то такая матрица называется антисимметричной
(др. название
–кососимметричной).
Элементы антисимметричной матрицы,
расположенные симметрично относительно
главной диагонали, противоположны
,
то такая матрица называется антисимметричной
(др. название
–кососимметричной).
Элементы антисимметричной матрицы,
расположенные симметрично относительно
главной диагонали, противоположны
![]() ,
,
а элементы главной
диагонали равны нулю
![]() .
.
Задача 1.
Докажите свойство
![]() .
.
Задача 2.
Докажите,
что всякую квадратную матрицу можно
представить в виде суммы симметричной
и антисимметричной матрицы:
![]() ,
где
,
где
![]() - симметричная матрица,
- симметричная матрица,
![]() -антисимметричная
матрица.
-антисимметричная
матрица.
Задача 3. Докажите, что всякую функцию можно представить в виде суммы четной и нечетной функций.
Задача 4. Докажите, что произведение двух антисимметричных матриц и является симметричной матрицей, в случае, если матрицы и коммутативны.
След матрицы. Введем операцию вычисления следа матрицы. Обозначается след матрицы символом
 .
.
ОПРЕДЕЛЕНИЕ. Сумма диагональных элементов квадратной матрицы называется следом матрицы:
![]()
Замечание. Фактически операция вычисления следа матрицы представляет собой задание на множестве квадратных матриц числовой функции под названием след матрицы
![]() .
.
Свойства следа произведения матриц:
![]()
1-ое свойство: под знаком следа - произведение двух матриц коммутативно.
2-ое свойство: под знаком следа - произведение трех матриц удовлетворяет свойству циклической перестановки.
Задача 5. Докажите
свойство
![]() .
Под знаком
следа матрицы произведение двух матриц
коммутативно.
.
Под знаком
следа матрицы произведение двух матриц
коммутативно.
Прямая сумма матриц.
Рассмотрим
квадратные матрицы
и
порядка
.
Определим прямую
сумму этих
матриц. Прямая
сумма
обозначается символом
![]() - знак сложения в круге.
- знак сложения в круге.
Итак:
![]() ,
где матрица
,
где матрица
![]() имеет следующий вид
имеет следующий вид
![]()
![]() .
.
Следовательно,
матрица
будет иметь порядок
![]() .
Очевидно,
.
Очевидно,
![]() ,
,
т.е. результат вычисления прямой суммы двух матриц зависит от порядка следования матриц и при сложении. Таким образом, операция вычисления прямой суммы не коммутативна.
Следует отметить, что матрица имеет блочную структуру, в данном случае матрица имеет блочно-диагональный вид: по главной диагонали расположены матрицы и , а по второстепенной (не главной) – нулевые матрицы .
ЛЕКЦИЯ 2
Определитель
матрицы. Минор и алгебраическое
дополнение. Теорема 1. Лапласа,
Теорема 2. О
![]() .
Обратная
матрица.
.
Обратная
матрица.
-
“Можно понять математику, когда она есть, но из понятия математика не вытекает ни одно математическое понятие”
Определитель матрицы.
Каждой квадратной
матрице можно поставить в соответствие
некоторое число, называемое определителем
матрицы
и обозначаемое символом
![]() .
Следовательно, на множестве квадратных
матриц мы можем задать числовую функцию
под названием определитель
матрицы.
Символически числовая функция
записывается так
.
Следовательно, на множестве квадратных
матриц мы можем задать числовую функцию
под названием определитель
матрицы.
Символически числовая функция
записывается так
![]() ,
,
где
![]() -
множество квадратных матриц порядка
-
множество квадратных матриц порядка
![]() .
Заметим, что у прямоугольных матриц
определитель
не существует, определить
невозможно.
.
Заметим, что у прямоугольных матриц
определитель
не существует, определить
невозможно.
ОПРЕДЕЛЕНИЕ. Определителем матрицы называется число, которое сопоставляется каждой квадратной матрице по некоторому правилу вычисления.
Существуют два правила вычисления определителя матрицы.
1-ое правило вычисления.
Рассмотрим квадратную матрицу порядка с элементами . При разложении определителя матрицы по 1-ой строке правило вычисления определителя матрицы имеет вид:
![]() .
.
При
разложении по
![]() -ой строке:
-ой строке:
![]()
Разложение по j-ому столбцу:
![]()
Таким образом, вычислить определитель можно путем разложения, как по любой строке, так и по любому столбцу.
В формуле вычисления
определителя
величина
![]() называется минором
с чертой элемента
.
Минор с
чертой
это определитель
матрицы
,
у которой вычеркнуты (т.е. удалены)
-ая строка и
называется минором
с чертой элемента
.
Минор с
чертой
это определитель
матрицы
,
у которой вычеркнуты (т.е. удалены)
-ая строка и
![]() -ый
столбец.
-ый
столбец.
Введем величину
![]() .
Эта величина называется алгебраическим
дополнением элемента
.
Определитель
матрицы
можно записать через алгебраическое
дополнение:
.
Эта величина называется алгебраическим
дополнением элемента
.
Определитель
матрицы
можно записать через алгебраическое
дополнение:
![]()
Пример вычисления определителя матрицы 2-го порядка:
![]()
![]()
2-ое правило вычисления.
![]()
Здесь
-кратное
суммирование проводится по всем индексам
![]() от 1 до
,
причем индексы не должны совпадать.
Комбинация индексов
равная
от 1 до
,
причем индексы не должны совпадать.
Комбинация индексов
равная
![]() в величине
в величине
![]() считается начальной комбинацией, для
которой
считается начальной комбинацией, для
которой
![]() .
Все остальные комбинации индексов
получаются из начальной путем перестановки
индексов, причем при четном числе
перестановок величина
.
Все остальные комбинации индексов
получаются из начальной путем перестановки
индексов, причем при четном числе
перестановок величина
![]() ,
при нечетном -
,
при нечетном -
![]() .
.
Для матрицы 3-го порядка определитель равен

Замечание: Если применить 1-ое правило вычисления определителя матрицы к вычислению миноров с чертой, то в результате мы получим выражение, которое в точности совпадет с результатом применения 2-го правила вычисления. Таким образом, оба правила вычисления определителя матрицы эквивалентны. Можете проверить это для определителя матрицы третьего порядка.
ОПРЕДЕЛЕНИЕ.
Квадратная
матрица
,
у которой
определитель равен нулю,
![]() ,
называется вырожденной.
,
называется вырожденной.
![]() ,
то матрица называется невырожденной.
,
то матрица называется невырожденной.
Рассмотрим миноры 2-х типов - миноры с чертой и миноры без черты.
Минор с чертой:
![]() -
это определитель
матрицы
,
у которой
вычеркнуты строки
-
это определитель
матрицы
,
у которой
вычеркнуты строки
![]() и вычеркнуты столбцы
и вычеркнуты столбцы
![]() .
.
Минор без черты:
![]() -
это определитель
матрицы,
составленной из элементов матрицы
,
стоящих на
пересечении строк
и столбцов
-
это определитель
матрицы,
составленной из элементов матрицы
,
стоящих на
пересечении строк
и столбцов
![]() .
.
Здесь индекс
![]() .
.
ТЕОРЕМА 1. Теорема
Лапласа (1749-1827).
Для любых строк
и столбцов
, причем
![]() ,
имеем
,
имеем
![]()
![]()
![]()
Теорема без доказательства.
Свойства определителей.
Равноправие строк и столбцов:
![]() .
.
