6

.1.СТРУКТУРНИЙ АНАЛІЗ КОНВЕЙЄРА

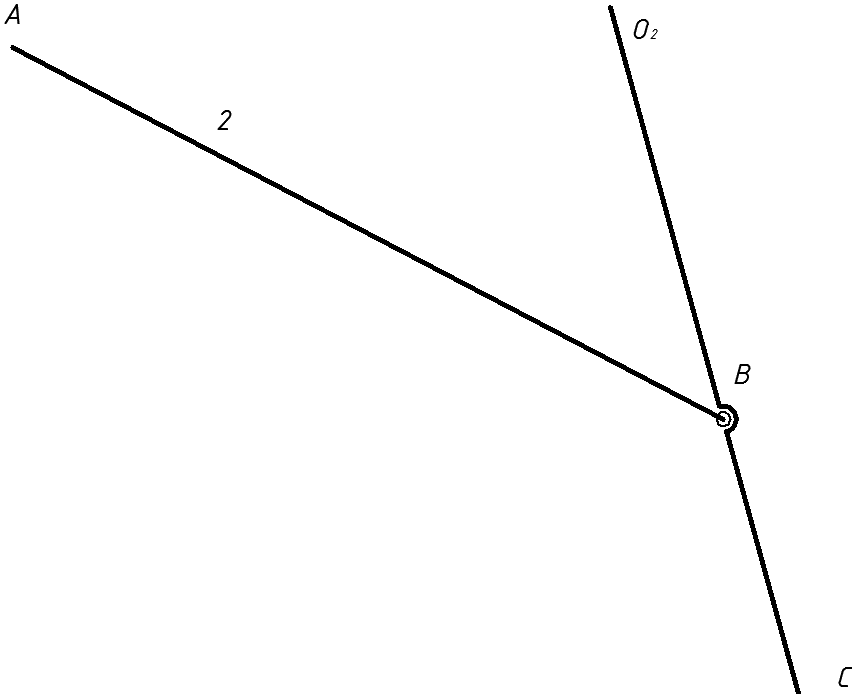
Механізм конвеєра (рис. 1.1) має в своєму складі рухомі ланки 1,2,3,4,5 і одну нерухому- стояк 6, він відноситься до стержньових, або важільних механізмів.

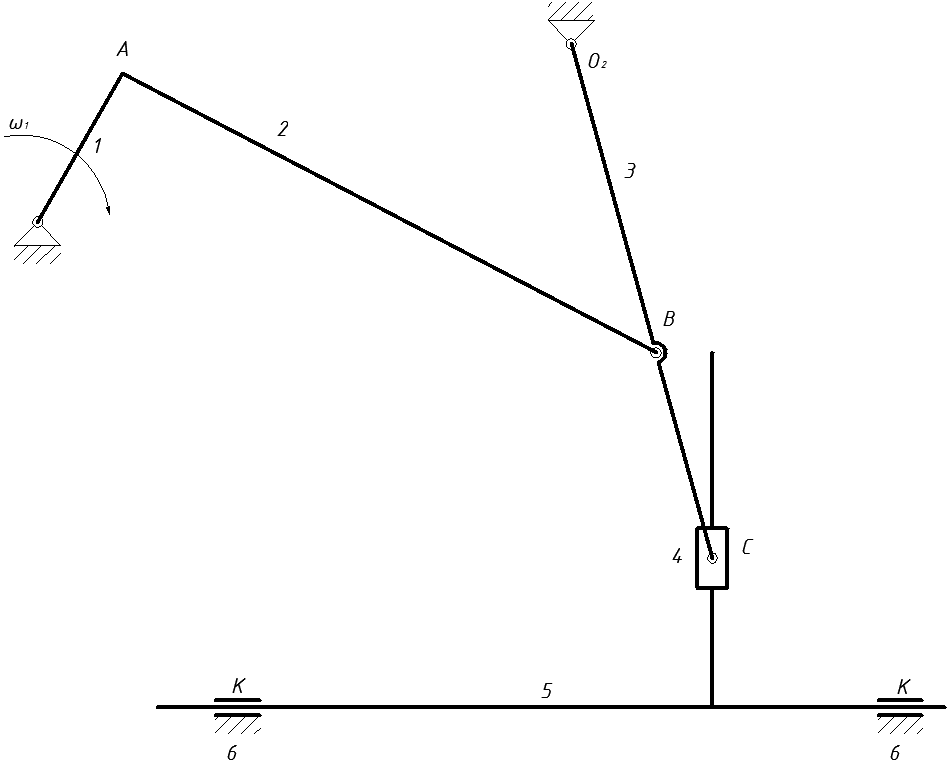
Рис. 1.1. Схема механізму конвеєра

Результати аналізу кінематичного ланцюга механізму конвеєра наведені в наступній таблиці:

Характеристики ланок і кінематичних пар механізму конвеєра

Ланки механізму			Кінематичні пари
Позн.	Назва	Характер руху	Позн.	Назва	Ланки, що створ.КП	Клас КП
1	Кривошип	Обертальний	О1	Оберт,нижча	1,6	v
2	Шатун	Плоскопарал.	А	Оберт,нижча	1,2	v
3	Коромисло	Коливальний	В	Оберт,нижча	2,3	v
4	Повзун	Плоскопарал.	О2	Оберт,нижча	3,6	v
5	Повзун	Поступальний	С	Поступ,нижча	4,5	v
6	Стояк	--------------	С	Поступ,нижча	3,7	v
			К		5,6	v

Cтепінь рухомості механізму конвеєра визначимо за формулою Чебишева

,

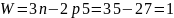де: n=5- кількість рухомих ланок механізму;

p₅=7- кількість кінематичних пар 5 класу;

У складі механізму конвеєра маємо одну вхідну ланку- кривошип О1 А- і дві групи Ассура. Спочатку виділимо групу №1, що складена із ланок 4,5 (рис.1.2, а), а потім групу №2 у складі ланок 2,3 (рис.1.2, б). Вхідна ланка 1разом із стояком 6 створює механізм 1 класу (рис.1.2, в).

Кожна ланка в обох групах Ассура входить в дві кінематичні пари, тому всі ланки являють собою контури 2 класу і обидві групи Ассура, а також механізм конвеєра в цілому – 2-ог класу.

Формула будови механізму конвеєра має вигляд:

I(1,6)← II (2,3)← II(4,5)

Обидві групи Ассура являють собою групи другого порядку, оскільки з’єднуються з вихідним механізмом в двох точках: А, О2 і С,К (див.рис.1.1)

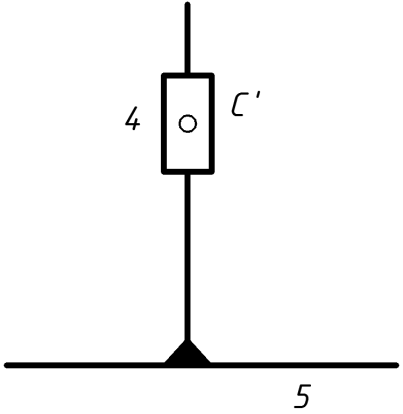
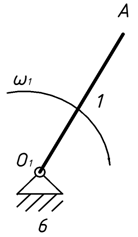
Група Ассура №1 Група Ассура №2 Механізм I класу

Клас II ланки 4,5 Клас II ланки 2,3 ланки 1,6

А) Б) В)

Рис. 1.2 Структурні складові механізму конвеєра

2. Синтез кінематичної схеми механізму конвейєра

В основі досліджуваного механізму конвеєра лежить механізм шарнірного чотириланковика (рис.2.1), то ж метою синтезу безпосередньо його кінетичної схеми за величиною коефіцієнта зміни середньої швидкості вихідної ланки к=1,2 є визначення довжин кривошипа 1 і шатуна 2.

Для однозначного розв’язання згаданої задачі потрібні наступні дані:

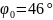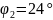кути і , що визначають крайні положення коромисла 3 в його зворотно-обертальному русі;

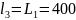мм – повна довжина коромисла 3 і абсциса центра 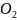його повороту відносно осі 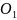обертання кривошипа 1 відповідно;

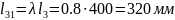- розрахована довжина коромисла 3 (довжина його ділянки );

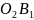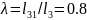- співвідношення довжин ділянок і 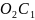коромисла 3.

За наявності наведених вихідних даних в першу чергу визначимо кут перекриття

,

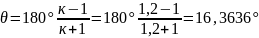тобто кут між напрямами 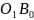і 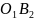, які створюються кривошипом 1 і шатуном 2 в їх двох крайніх положеннях.

Постійність значень θ і К можна забезпечити, якщо центр обертання кривошипа 1 розміщувати в будь-якій точці кола L, відносно якого пряма 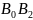є хордою, на неї спирається вписаний в загальне коло кут θ. Центр кола L розташований на відрізку В’ , він є перпендикуляром до хорди і проходить через її середню точку В’. Радіус кола L становить

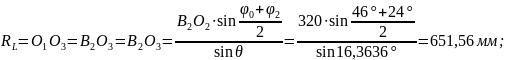
тут слід нагадати, що вписаному в коло L куту θ відповідає центральний кут .

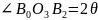Якщо положення осі обертання кривошипа 1 зафіксувати відносно центра розміром

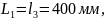
то із 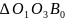і 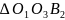слід, по-перше

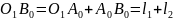, (1)

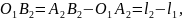
а по-друге

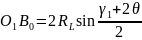, (2)

.

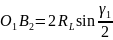На підставі системи рівнянь (1) маємо

,

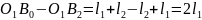звідси слід

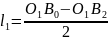
і далі

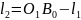. (3)

Для визначення довжини відрізків і за допомогою системи рівнянь (2) послідовно знайдемо

;

;

;

;

.

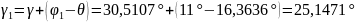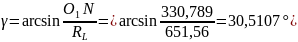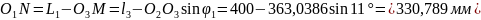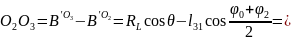
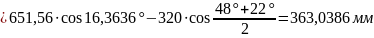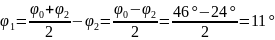Тепер визначимо

;

.

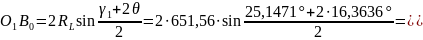
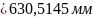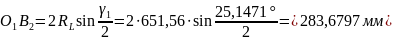На підставі рівняння (3) отримаємо довжини кривошипа 1 і шатуна 2 відповідно

;

.

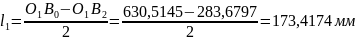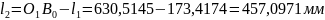Для подальших розрахунків приймаємо

.

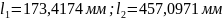Зрозуміло, що зображення кінематичної схеми механізму конвеєра за зразком рис. 1 на першому листі графічної частини курсового проекту можна виконувати лише після визначення довжини кривошипа 1 і шатуна 2. Схему механізму слід виконувати з використанням лінійного маcштабу

в трьох положеннях, які визначаються наступними індексами:

0 – початкове положення з кутом установки 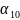кривошипа 1, що

відповідає початку прямого (робочого) ходу повзуна 5;

1 – досліджуване розгорнуте положення механізму з кутом установки кривошипа ;

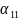2 – друге крайнє положення механізму, що відповідає закінченню прямого ходу повзуна 5 і куту 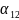установки 1.

Видно, що наведені індекси являють собою другу цифру у складі індексу кута 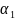установки кривошипа 1. Розгорнуте положення механізму слід виконати з урахуванням кута , який призначається керівником курсового проектування.

За наявності зазначеного креслення довжини кривошипа 1 і шатуна 2 можна визначити графічним шляхом, з цією метою перше рівняння системи (3) представимо у формі

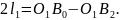(4)

після чого на кресленні кінематичної схеми механізму за допомогою дуги кола із центром в точці перенесемо точку 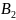на відрізок прямої , тобто побудуємо різницю

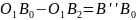
або праву частину рівняння (4). Після вимірювання відрізка 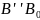на кресленні і поділу результату на впіл визначимо дійсну довжину кривошипа

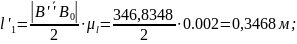
тут - масштаб креслення.

Довжина шатуна

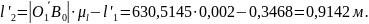
Результати визначення довжин кривошипа 1 і шатуна 2 двома методами слід порівняти між собою, тобто визначити відносні відхилення

,

.

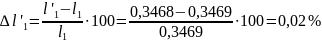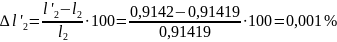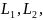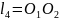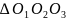Положення осі повороту коромисла 3 відносно осі обертання кривошипа 1 слід визначити координатами вони необхідні для обробки корпуса механізму конвейєра на горизонтально-розточувальному верстаті і визначають собою міжосьову відстань . Із слід

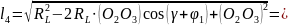
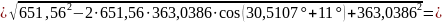
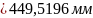
За результатами вимірювання на креслені

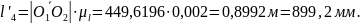
Відхилення від розрахункового значення

.

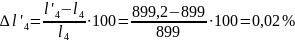Абсцис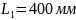а обрана раніше, ордината осі відносно центра обертання кривошипа

;

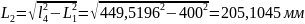надалі приймаємо

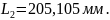
За результатами вимірювання на кресленні

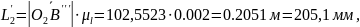
відхилення від розрахункового значення

.

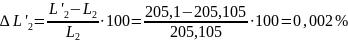Конструктивний розмір 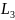визначається за емпіричним співвідношенням

;

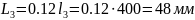приймаємо