10) Условия интерференционных максимумом и минимумов, выраженное через длину волны и разность фаз колебаний.

11) Интерференция на плоскопараллельной пластине.

Получить две когерентные волны можно и другим методом - делением амплитуды первичной волны.

Если световая волна с плоским фронтом падает на плоскопараллельную пластину, то она отражается и преломляется на обеих сторонах пластины (рис. 3.3). Будем рассматривать волны 1 и 2. Эти волны имеют одинаковые частоты  . Разность фаз  , т.к. она определяется только условиями отражения и преломления. Следовательно, волны 1 и 2 когерентны. Их разность хода  , где   - толщина пластины,   - ее показатель преломления,   - угол падения. Волны 1 и 2 параллельны. Это означает, что они сходятся только на бесконечности и там образуют интерференционную картину, которую называют линиями равного наклона.

Интерференция света в плоскопараллельной пластине

В оптических экспериментах, где толщина пластин мала (у нас d≈0,1 мм), бесконечно далекое расстояние до экрана наблюдения соответствует нескольким метрам.

Для наблюдения изображения интерференционной картины можно воспользоваться линзой.

12) Кольца Ньютона-пример интерференционных полос равной толщины.

Кольца Ньютона - пример полос равной, толщины. Они наблюдаются при отражении света. от соприкасающихся друг с другом плоско параллельной толстой стеклянной пластинки и плоско выпуклой линзы с большим радиусом кривизны. Роль тонкой пленки переменной толщины b, от поверхности которой отражаются когерентные волны, играет зазор между пластинкой и линзой. Пусть показатель преломлений зазора n, толщина в точке Е равна b. Параллельный пучок света падает       нормально (i₁ = 0°) на плоскую поверхность ВС линзы и отражается от верхней и нижней поверхности зазора (от т. Е и F ). Найдем, радиус колец Ньютона r.

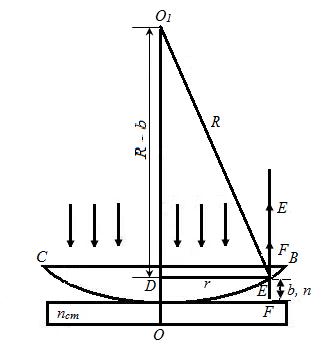
Оптическая разность хода между лучами, отраженными от верхней и нижней поверхности зазора равна

                                    (n < n_ст)

λ/2 учитывает сдвиг по фазе на  π при отражении от оптически более плотной среды в т. F.            

Из треугольника О₁ДЕ следует

Тогда

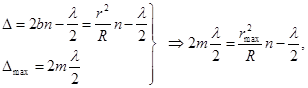
радиус колец Ньютона для отраженного света.

радиус колец Ньютона для проходящего света.

Пример:

Допустим, что толщина пластинки не постоянной (∼b, n = const).

Т огда во всех тех местах пластинки, где толщина b, а следовательно, и разность хода Δ одинаковы, наблюдается один и тот же результат интерференции. Это означает, что вдоль какой-либо темной или светлой интерференционной полосы, образующейся на поверхности, толщина этой пластинки одна и та же.

Полосы равной толщины локализованы на поверхности пластинки. При наблюдении в белом свете полосы будут окрашены так, что поверхность содержит все цвета радуги. Пример полос равной толщины: нефтяные пятна, мыльные пленки и т.д.

13) Формулировка принципа Гюйгенса-Френеля.

Если на пути световой волны находятся непрозрачные тела или экраны с отверстиями, то грубые наблюдения показывают, что за этими телами образуется область тени. Эту область можно очертить геометрически, полагая, что свет распространяется прямолинейно, световые лучи есть прямые линии.

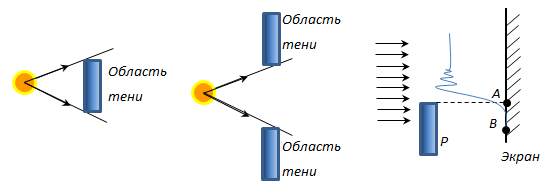Более детальное наблюдение показывает, что световые волны заходят в область геометрической тени, причём на границе между областями света и тени появляются чередующиеся максимумы и минимумы света, свидетельствующие о некотором перераспределении световой энергии на этой границе. Это огибание световыми волнами границ непрозрачных тел е образованием интерференционного перераспределения энергии по различным направлениям называется дифракцией волны. 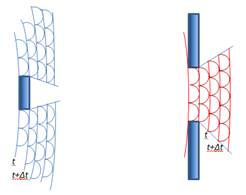(Или: Явление, возникающие при р аспространении света в среде с резкими неоднородностями, называется дифракцией света.)

Явление дифракции можно объяснить, пользуясь принципом Гюйгенса: каждая точка пространства до которой доходит волновое движение (т.е. фронт волны) является источником вторичных волн, огибающая которых дает положение фронта волны в следующий момент времени. В однородной среде вторичные волны будут представлять полусферы, направления распространения вторичных волн совпадает с  направлением распространения первичной волны.  Задачу о распределении энергии вдоль фронта волны можно решить воспользовавшись принципом Гюйгенса-Френеля:

а)принцип Гюйгенса;

б)источники вторичных волн когерентны;

в)амплитуда dA колебаний, возбуждаемых в точке М вторичным источником, пропорциональна отношению площади dS участка волновой поверхности S к расстоянию r от него до т. М, и зависит от угла α между внешней нормалью к волновой поверхности и направлением от элемента dS в точку М.

                                 

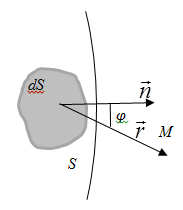
K(φ) - коэффициент пропорциональности, зависящий от угла φ.

При φ = 0 K(φ) = max, при φ = π/2 K(φ) = 0.

Результирующее поле в т. М представляет собой суперпозицию колебаний (1), взятых для всей волновой поверхности:

-

--аналитическая запись принципа Гюйгенса - Френеля.