
- •Найти наименьшее и наибольшее значения функции на отрезке [0;5].
- •Тема “ Приложения дифференциального исчисления ” Вариант № 3.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 4.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 5.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 6.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 7.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 18.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 19.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 20.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 24.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 25.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 28.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 29.
- •Найти наименьшее и наибольшее значения функции на отрезке .
- •Тема “ Приложения дифференциального исчисления ” Вариант № 30.
- •Найти наименьшее и наибольшее значения функции на отрезке .
Найти наименьшее и наибольшее значения функции на отрезке .
На оси параболы
 дана точка на расстоянии 7 от вершины.
Указать абсциссу ближайшей к ней точки
кривой.
дана точка на расстоянии 7 от вершины.
Указать абсциссу ближайшей к ней точки
кривой.
Тема “ Приложения дифференциального исчисления ”
Вариант № 17.
Вычислить пределы по правилу Лопиталя:
1.
 ;
3.
;
3.
![]() ;
;
2.
 ;
4.
;
4.
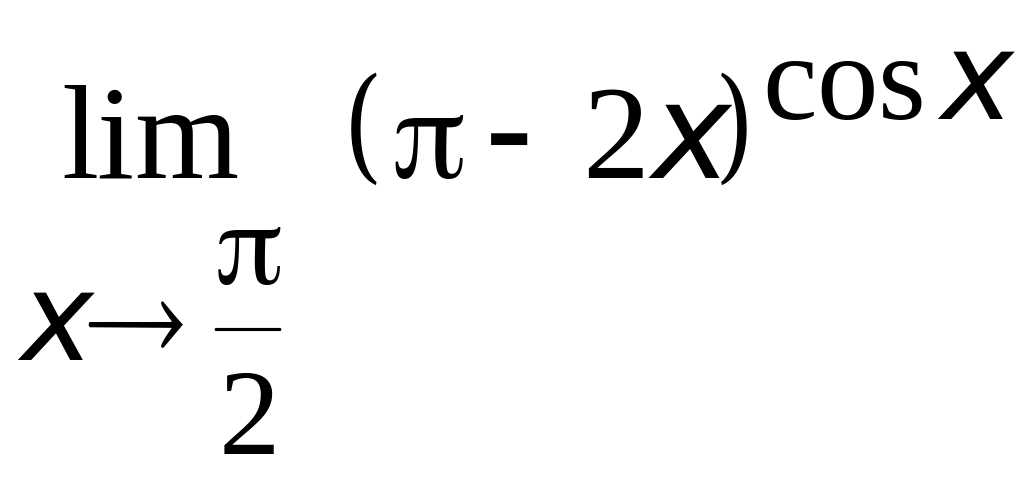 .
.
Исследовать функции и построить их графики:
5.
 ;
6.
;
6.
![]() .
.
Найти наименьшее и наибольшее значения функции на отрезке .
Требуется сделать жестяное корыто, имеющее форму прямого кругового цилиндра, разрезанного вдоль оси симметрии. Каковы должны быть размеры этого корыта, чтобы при одном и том же количестве материала (S=12π) вместимость его была наибольшей?
Тема “ Приложения дифференциального исчисления ” Вариант № 18.
Вычислить пределы по правилу Лопиталя:
1.
 ;
3.
;
3.
![]() ;
;
2.
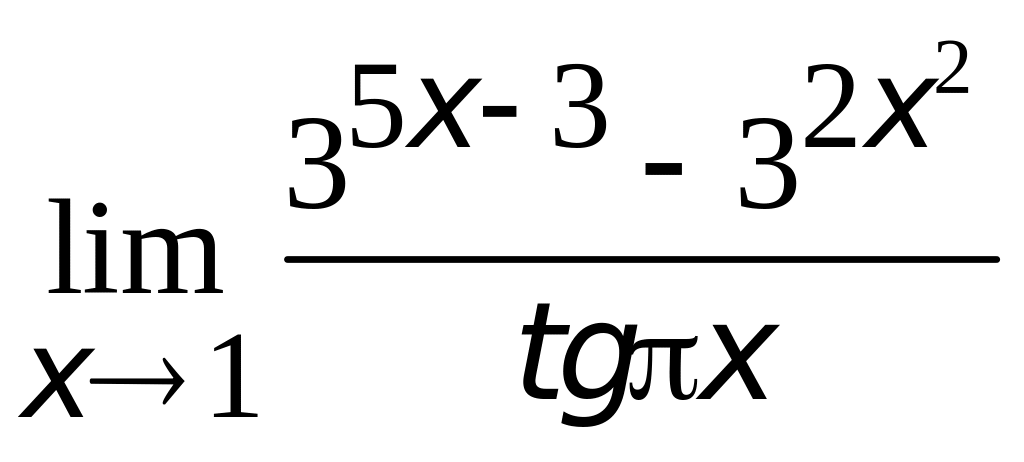 ;
4.
;
4.
 .
.
Исследовать функции и построить их графики:
5.
![]() ;
6.
;
6.
![]() .
.
Найти наименьшее и наибольшее значения функции на отрезке .
Открытый сосуд состоит из цилиндра, заканчивающегося снизу полусферой. Толщина стенок постоянна. Каковы должны быть размеры сосуда, чтобы при данной вместимости (V=18π) на него пошло минимум материала.
Тема “ Приложения дифференциального исчисления ” Вариант № 19.
Вычислить пределы по правилу Лопиталя:
1.
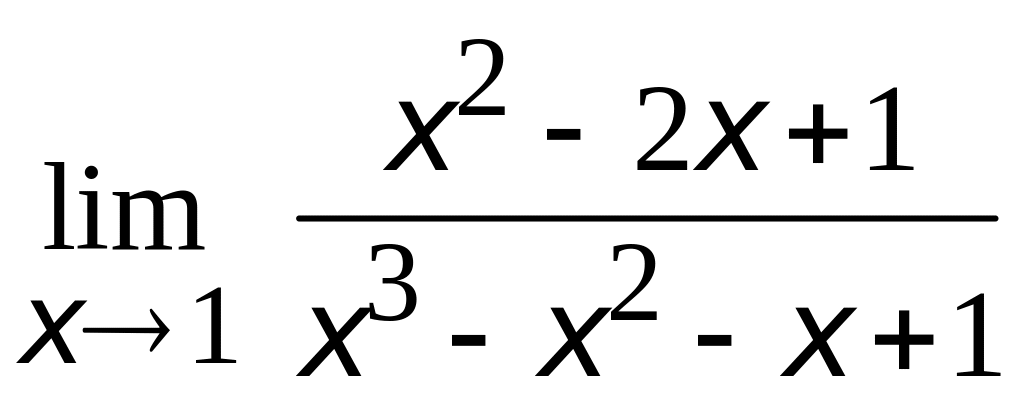 ;
3.
;
3.
![]() ;
;
2.
![]() ;
4.
;
4.
 .
.
Исследовать функции и построить их графики:
5.
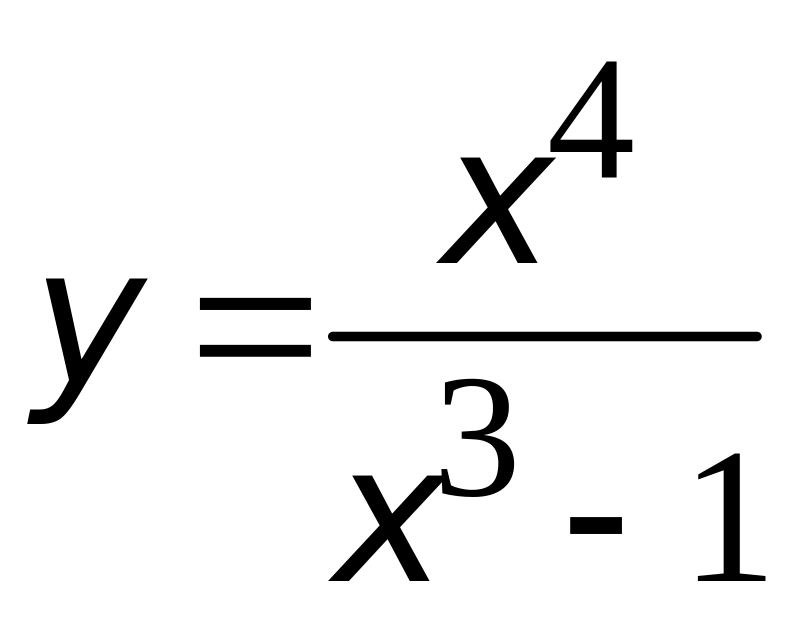 ;
6.
;
6.
![]() .
.
Найти наименьшее и наибольшее значения функции на отрезке .
Какими должны быть размеры кастрюли без крышки, чтобы при одном и том же количестве материала (S=78π), затраченного на ее изготовление, она имела наибольшую вместимость?
Тема “ Приложения дифференциального исчисления ” Вариант № 20.
Вычислить пределы по правилу Лопиталя:
1.
 ;
3.
;
3.
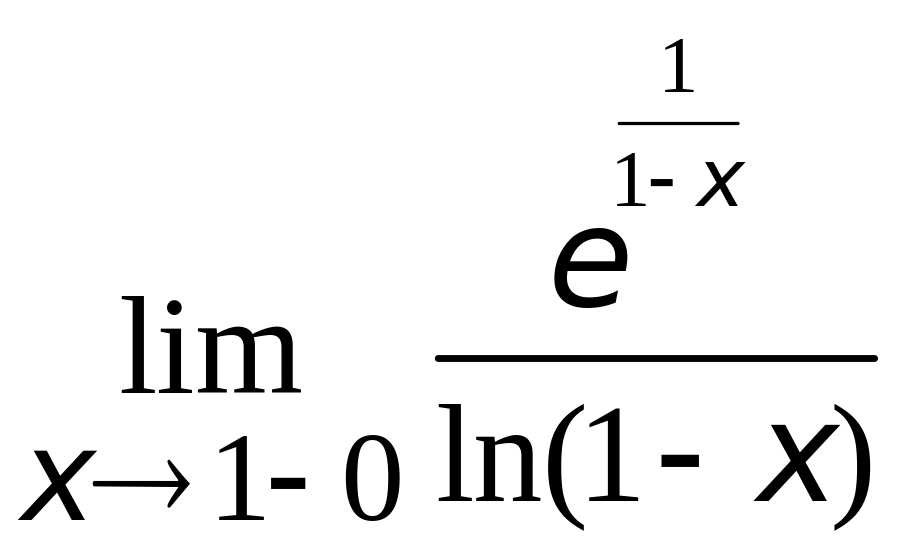 ;
;
2.
![]() ;
4.
;
4.
![]() .
.
Исследовать функции и построить их графики:
5.
![]() ;
6.
;
6.
![]() .
.
Найти наименьшее и наибольшее значения функции на отрезке .
Требуется сделать коническую воронку, с образующей
 20
см. Какой должна быть высота воронки
h,
чтобы ее объем был наибольшим?
20
см. Какой должна быть высота воронки
h,
чтобы ее объем был наибольшим?
Тема “ Приложения дифференциального исчисления ”
Вариант № 21.
Вычислить пределы по правилу Лопиталя:
1.
 ;
3.
;
3.
![]() ;
;
2.
![]() ;
4.
;
4.
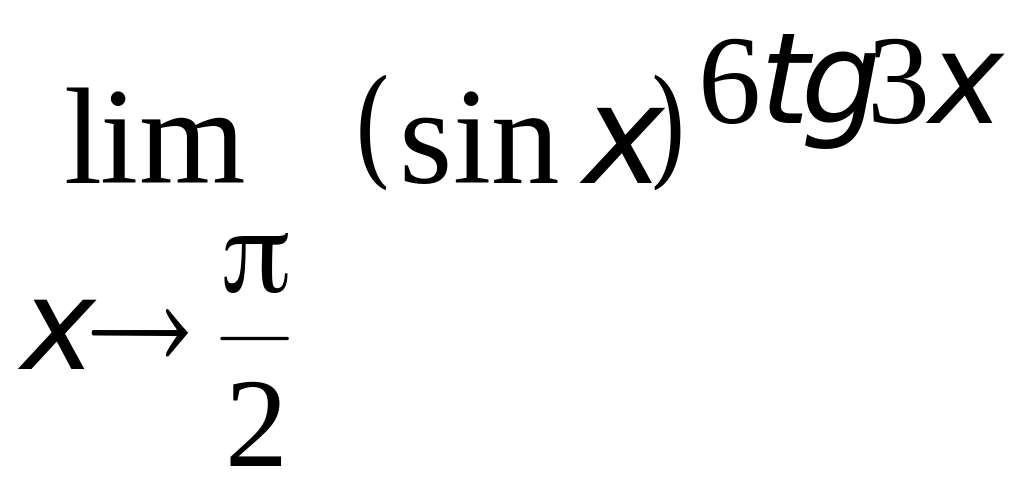 .
.
Исследовать функции и построить их графики:
5.
;
6.
![]() .
.
Найти наименьшее и наибольшее значения функции на отрезке .
Определить наибольшую площадь прямоугольника, вписанного в полукруг радиуса 3.
Тема “ Приложения дифференциального исчисления ”
Вариант № 22.
Вычислить пределы по правилу Лопиталя:
1.
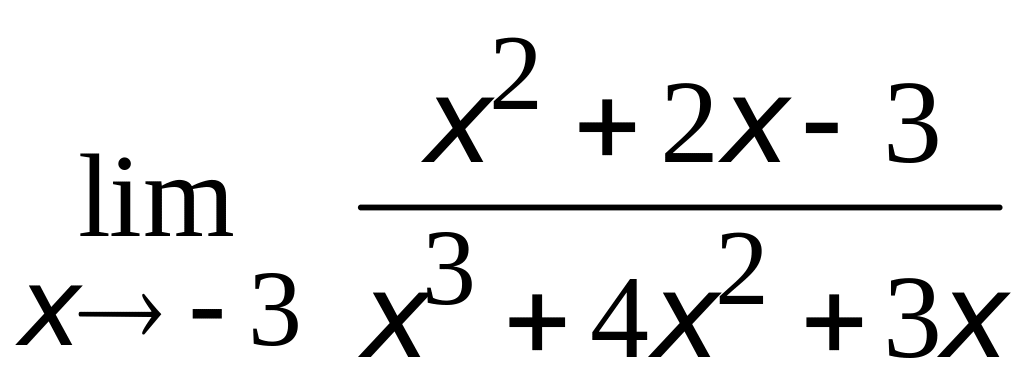 ;
3.
;
3.
![]() ;
;
2.
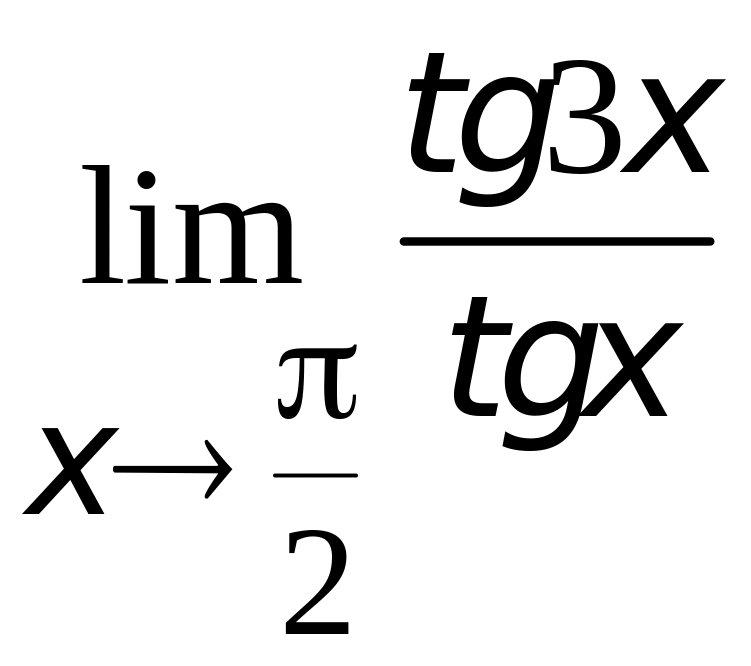 ;
4.
;
4.
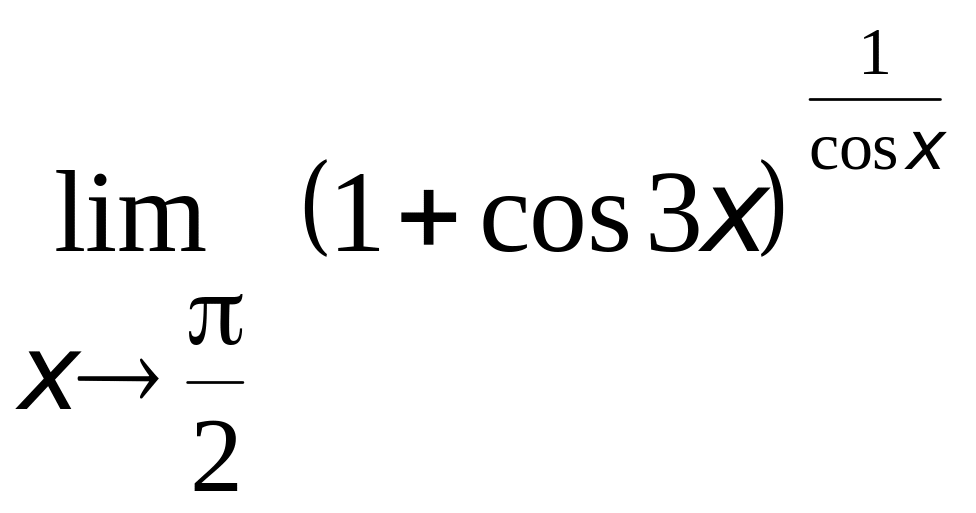 .
.
Исследовать функции и построить их графики:
5.
 ;
6.
.
;
6.
.
Найти наименьшее и наибольшее значения функции на отрезке .
Из фигуры, ограниченной кривой
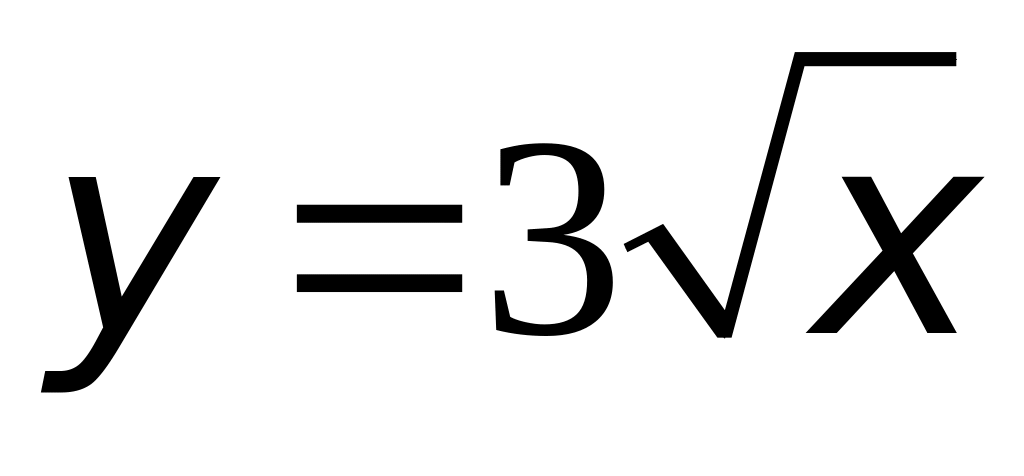 и прямыми x
= 4 и y
= 0, вырезать прямоугольник наибольшей
площади.
и прямыми x
= 4 и y
= 0, вырезать прямоугольник наибольшей
площади.
Тема “ Приложения дифференциального исчисления ”
Вариант № 23.
Вычислить пределы по правилу Лопиталя:
1.
 ;
3.
;
3.
![]() ;
;
2.
![]() ;
4.
;
4.
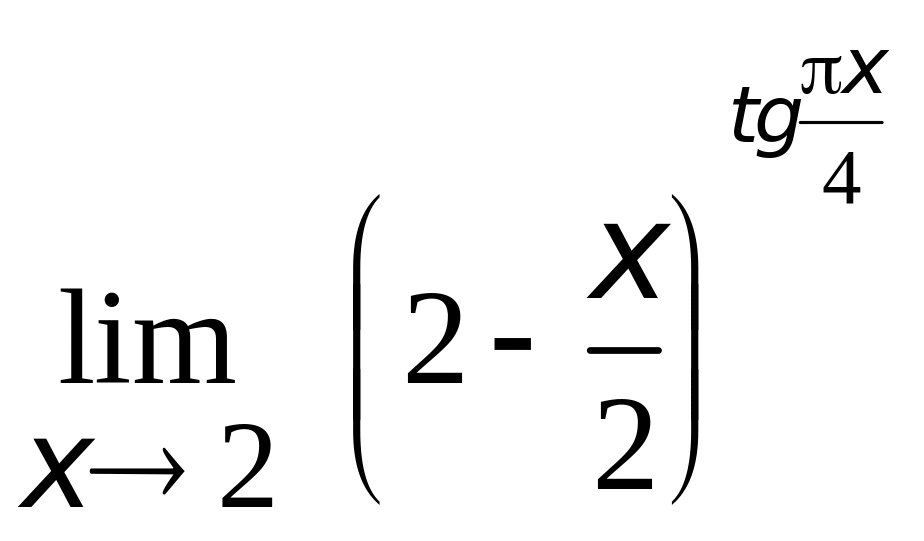 .
.
Исследовать функции и построить их графики:
5.
;
6.
![]() .
.
