1.2.3. Определение угловых скоростей звеньев.

Угловое ускорение ₁ ведущего звена, совершающего равномерное движение, равно нулю.

Угловое ускорение звена 2-3 с^-2 ,

с^-2 (2.35)

с^{-2 (по часовой )}

Для определения направления углового ускорения ₂ звена 2 надо мысленно перенести вектор тангенциального ускорения в точку С. В направлении этого вектора точка B вращается относительно точки С против часовой стрелки. Знак плюс.

По аналогии определяем значение и направление углового ускорения звена 3 :

1.3.1.Силовой анализ.

В задачу силового исследования входит определение:

1) сил, действующих на звенья механизма;

2) реакций в кинематических парах;

3) уравновешивающей силы (момента).

Силовой анализ основан на принципе Даламбера. Сущность его заключается в том, что каждое звено может рассматриваться в условном статическом равновесии, если к нему помимо всех действующих внешних сил приложить инерционную нагрузку в виде силы инерции и момента пары сил инерции. При этом условии для каждого звена справедливы равенства:

, (3.1)

поэтому неизвестные силы (реакции в кинематических парах) могут определяться методом статики.

Для проведения силового анализа кинематическая цепь должна быть статически определимой, т. е. число неизвестных параметров реакций должно быть равно количеству уравнений статики, которые можно составить для их определения.

Начинать силовой анализ необходимо с наиболее удаленной от ведущего звена структурной группы.

1. Определение сил тяжести звеньев.

Исходя из начальных данных, определяем силы тяжести звеньев механизма. Векторы сил будут направлены из соответствующих центров тяжести, H :

(3.2)

2. Определение сил перегрузки.

Коэффициент горизонтальной перегрузки равен .Отсюда вычисляем силы перегрузки, действующие на звено BC из вено СD и направленные так же из центров тяжести соответствующих звеньев, H:

(3.3)

3. Определение сил инерции и моментов инерции.

Силы инерции второго звена BC и третьего звена СD равны.

(3.4)

Знак минус показывает, что эти силы направлены в сторону , противоположную направлениям ускорения этих точек.

Моменты инерции равны:

(3.5)

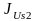Где и - моменты инерции звеньев относительно центров масс и , они находятся по формуле : (3.6)

Направлены моменты инерции в сторону, противоположную направлению угловых ускорений.

4. Определение реакций в кинематических парах.

Выделяем из механизма структурную группу и прикладываем к ней все внешние силы и реакции. Реакции и раскладываем на две составляющие.

(3.7)

Где и - реакции направленные перпендикулярно звеньям.

и -реакции направленные вдоль соответствующих звеньев.

_{Для определения значения силы сопротивления} построим график зависимости этой силы от угла поворота звена CD . Покажем на графике известные нам точки при _{и соединим их кривой. Зная угол поворота выбранного положения, можно вычислить нужную аэродинамическую силу для выбранного положения равно}

_(3.8)

_Отсюда

_{1)Составляем сумму моментов всех сил и реакций звена BC относительно точки С.}

_(3.9)

_(3.10)

_{Где h – плечи сил, т.е перпендикуляры к линиям действия соответствующих сил , показанные в масштабе на чертеже.}

_{Отсюда находим неизвестную реакцию.}

_(3.11)

_{2) Составляем сумму моментов всех сил и реакций звена CD относительно точки С.}

_(3.12)

_{Уравнение равновесия имеет вид}

_{( 3.13)}

_(3.14)

_{Построение плана сил структурной группы начинаем с проведения линии действия реакции .Далее в выбранном масштабе К на произвольной точке линии действия реакции откладываем отрезки, соответствующих силам и реакциям. Чтобы выбрать масштаб возьмем произвольный отрезок}

_(3.15)

Теперь находим длину откладываемых отрезков, мм:

_(3.16)

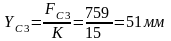
_{Затем проводим линию действия реакции до пересечения с первоначальной линией, т.е. линией действия реакции . Можно определить через уже известные отрезки, следующие реакции:}

_(3.17)

_{4) Для определения внутренний реакции со стороны звена СD на звено BC запишем уравнение равновесия второго звена ВС.}

_(3.18)

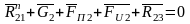_(3.19)

_{В этом уравнении неизвестна реакция . Соединяя на плане сил начало вектора c концом вектора , определим отрезок, соответствующий реакции}

_(3.20)

_(3.21)

_{5) Определение сил и уравновешивающего момента, приложенных к входному звену.}

_{Рассмотрим равновесие первого звена AB, т.к. вес и силу инерции мы не учитываем , в виду их малой величины, то на звено AB действуют неизвестный по величине и направлению реакция. ; Реакция равная реакции , но противоположная по направлению ; уравновешивающий момент}

_(3.22)

_{Составим сумму моментов относительно точки A}

_{(3.23 )}

_(3.24)

_(3.25)

_{Отсюда выясняем}

_(3.26)

_{6) Рычаг Жуковского.}

_{Теперь определим уравновешивающий момент по теореме Жуковского. Для этого план скоростей поворачиваем на . Затем параллельно самим себе переносим все заданные активные силы в одноименной точке повернутого плана скоростей. Предварительно перед этим все моменты, приложенные к звеньям, должны быть заменены парами сил , приложенных в шарнирах звеньев, которых действует заменяемый момент, перпендикулярно этому звену. Звено является плечом пары сил.}

_{( 3.27)}

_(3.28)

_{Cоставляем уравнение равновесия моментов, приложенных в соответствующих точках повернутого плана скоростей, относительно полюса.}

_{( 3.29)}

_{( 4.1) (4.2)}

_{Уравновешивающий момент равен:}

_{Моменты найденные в силовом анализе и с помощью рычага «Жуковского», не должны отличаться более чем на 10%. Проверим.}

_{Так как значение меньше 10% можно предположить, что уравновешивающий момент найден верно.}

24