Вопрос 1.

Основные уравнения, лежащие в основе расчета теплообменников.

Уравнение теплового баланса. Изменение энтальпии теп­лоносителя вследствие теплообмена определяется соотношением

dQ = Gdi,

где G—расход массы, кг/с; i — удельная энтальпия, Дж/кг; dQ изме­ряется в Дж/с или Вт.

Для конечных изменений энтальпии, полагая, что расход массы не­изменен,

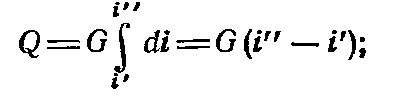
здесь i" и i’ — начальная и конечная энтальпии теплоносителя.

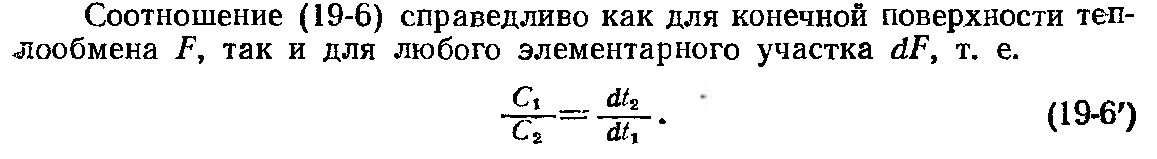
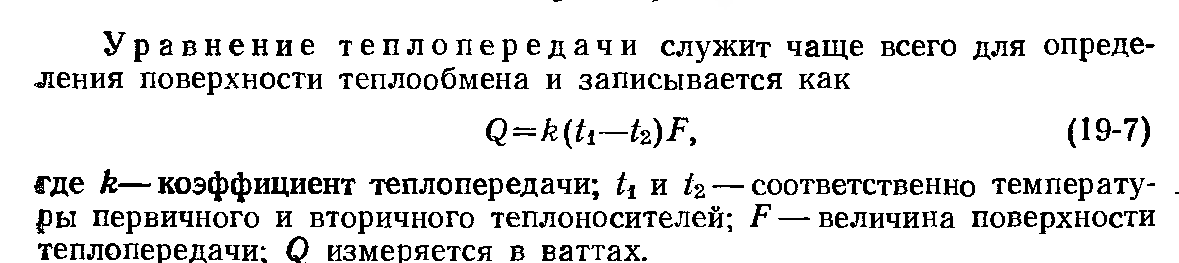
Вопрос 3

Составляющая потерь давления в каналах ТА.

Рассмотрев гидравлический расчет теплообменника, можем сказать, что потери давления в теплообменниках делятся на 2 вида: в межтрубном пространстве и во внутритрубном пространстве.

В межтрубном пространстве гидравлическое сопротивление составляют: вход и выход жидкости через штуцера , количество поворотов через сегментные перегородки и сопротивление трубного пучка при его поперечном или продольном обтекании.

Во внутритрубном пространстве гидравлическое сопротивление складывается из шероховатости труб, вход в камеру и выход из неё, количества поворотов на 180^о, входов в трубы и выходов из них .

Вопрос 5

Расчет конечных температур теплоносителей для прямоточного ТА.

А. Прямоточная схема движения теплоносителей.

Для вывода формул используем экспоненциальный закон изменения температурного напора вдоль поверхности теплообмена:

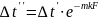
Если это уравнение записать в виде

То после несложных преобразований получим:

Или 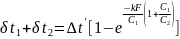(г)

Неизвестные величины и 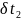определим из теплового баланса:

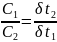
Откуда

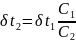
Подставив выражение для в уравнение (г), получим :

Ил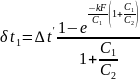и (и)

Из уравнения (и) следует, что изменение температуры первичного теплоносителя равно некоторой доле первоначального температурного перепада между теплоносителями (

Выражение 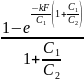является функцией только kF/C₁,C₁/C₂ и может быть заранее рассчитано и табулировано.

Аналогично для прямотока можно получить формулу для нахождения изменения температуры вторичного теплоносителя :

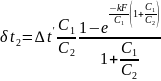(к) Окончательно формулы (и) и (к) можно записать так :

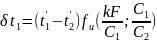
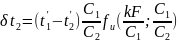
Вопрос 7.

Расчет конечных температур теплоносителей для противоточного ТА.

Противоточная схема течения движения теплоносителей

В качестве исходного уравнения для получения формулы для изменения температуры теплоносителей по длине поверхности берется уравнение применительно к противоточной схеме движения:

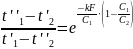
Дальнейшие выкладки такие же, как и для прямотока. Окончательные результаты имеют вид:

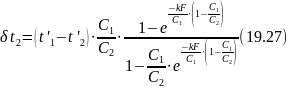
Если обозначить

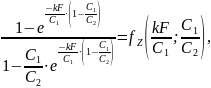
Тогда формулы (19.26) и (19.27) запишутся так:

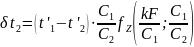
Количество переданной теплоты определяется для противотока как

Вопрос 11

Два метода расчета ТА. Число единиц переноса теплоты Ntu

Тепловой расчет ТА может быть проектным (конструкторским) и поверочным. Задача проектного расчета - определение величины и формы поверхности теплообмена, разделяющей горячую и холодную среды. Поверочный расчет выполняется в том случае, когда величина и форма поверхности задана, т.е. известна конструкция ТА. Задача поверочного расчета – определение количества передаваемой теплоты и конечных температур рабочих сред. Указанные задачи решаются двумя методами:

1 Метод среднего логарифмического температурного напора

2 Метод эффективности теплообменника по числу единиц переноса теплоты

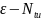
Принципиально методы базируются на уравнении теплового баланса и уравнении теплопередачи. Отличие лишь в выборе параметров.

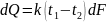Уравнение теплопередачи: , -коэфф.теплопередачи.

Уравнение теплового баланса:

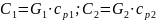
–водяные эквиваленты.

плюс - для прямотока; минус – для противотока.

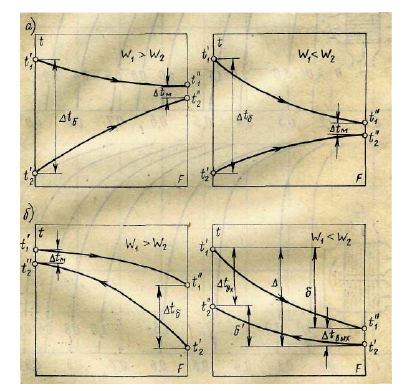
Зависимость темпер-ры теплоносителей от теплоемкости массовых расходов для прямоточной (а) и противоточной схемы (б) (W-это С)

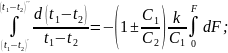
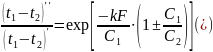
Из уравнения (*) видно, что отношение температурных напоров выходного к входному зависит от двух важных безразмерных параметров:

- число единиц переноса теплоты

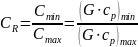
Тепловая эффективность (КПД) теплообменника 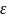определяется отношением теплопроизводительности аппарата 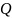к ее предельному значению :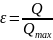

;

Если :

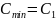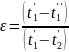
Если :

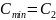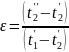
Обычно в теплообменниках

Для прямоточной схемы :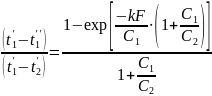

Для противоточной схемы:

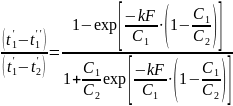
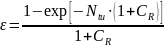
зависит от 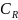и

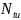
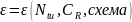
При расчете методом средних логарифмических температурных напоров применяется уравнение:

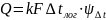
–поправка к среднелогарифмическому напору.

Если теплообменник противоточный, то Для всех остальных схем и он определяется схемой движения и двумя безразмерными параметрами Р и R.

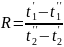
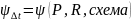
Если , то . Если , то

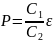
Из уравнения теплового баланса для всего теплообменника: ; .

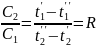Анализ методов и среднелогарифмического температурного напора показали, что они дают одинаковые расчеты, но метод менее трудоемок из-за отсутствия в нем последовательных приближений.