Прошитые бинарные деревья
Порядок обхода бинарного дерева можно хранить непосредственно в структуре данных, для чего достаточно ввести дополнительное поле указателя в элементе списковой структуры и хранить в нем указатель на узел, следующий за данным узлом при обходе дерева.
Представление деревьев в виде массивов также допускает хранение порядка прохождения дерева, для чего вводится дополнительный массив, в который записывается адрес узла в основном массиве, следующего за данным узлом.
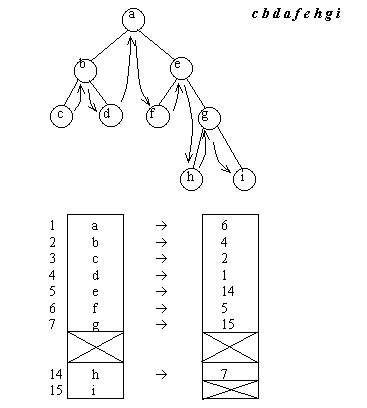
Такие структуры данных называются прошитыми бинарными деревьями. Указатели (адреса), определяющие порядок обхода, называются нитями. При этом в соответствии с порядком прохождения вершин различают право прошитые, лево прошитые и симметрично прошитые бинарные деревья.
Идеально сбалансированное бинарное дерево
Идеально сбалансированное бинарное дерево – это бинарное дерево, для каждого узла которого количество узлов в левом и правом поддеревьях отличается не более, чем на единицу.
Если распределять узлы поровну слева и справа от каждого узла, что свойственно для идеально сбалансированного дерева, то можно достичь минимальной высоты дерева при данном числе узлов, при этом на всех уровнях, кроме самого нижнего, необходимо располагать максимально возможное число узлов.
Рекурсивная процедура создания идеально сбалансированного дерева, представленного в виде списковой структуры (применяется правило равномерного распределения узлов при известном их количестве n: один узел является корнем, левое поддерево содержит nl = n div 2 узлов, правое поддерево содержит остальные узлы nr = n – nl – 1):
type
tree = ^node;
node = record
data: string[10];
left, right: tree;
end;
{ Создание идеально сбалансированного бинарного дерева для n узлов }
procedure Creat_tree( N: integer; var cur: tree);
var
pnt: tree;
nl, nr: integer;
begin
if n=0 then
cur:=Nil
else
begin
nl:=n div 2;
nr:=n-nl-1;
New(ptn);
writeln('Данные:');
readln(ptn^.data);
Creat_tree(nl,ptn^.left); { создание левого поддерева }
Creat_tree(nr,ptn^.right); { создание правого поддерева }
cur:=ptn; { включение узла в дерево }
end;
end;
Узлы дерева создаются в прямом порядке обхода вершин (вершина, левое поддерево, затем правое поддерево), поэтому исходные данные должны соответствовать прямому порядку обхода. А включаются в дерево узлы в обратном порядке, т. е. снизу вверх (от листьев к корню).