Представление бинарного дерева в виде массива
Полное бинарное дерево достаточно просто можно представить в виде массива, так как такое дерево всегда имеет строго определенное число узлов (вершин) на каждом уровне, которые нумеруются слева направо последовательно по уровням. Эти номера используются в качестве индексов в одномерном массиве. Если число уровней дерева в процессе обработки не будет существенно изменяться, то способ представления полного бинарного дерева в виде массива значительно более экономично, чем любая списковая структура. В результате структура дерева переносится в одномерный массив.
Для неполных бинарных деревьев применяют следующий способ представления: бинарное дерево дополняется до полного дерева, вершины последовательно нумеруются; в массив заносятся не только те вершины, которые были в исходном неполном дереве, – при таком представлении элемент массива выделяется независимо от того, будет ли он содержать узел исходного дерева; неиспользуемые элементы массива отмечаются занесением специального значения в соответствующие элементы массива. В результате структура дерева также переносится в одномерный массив.
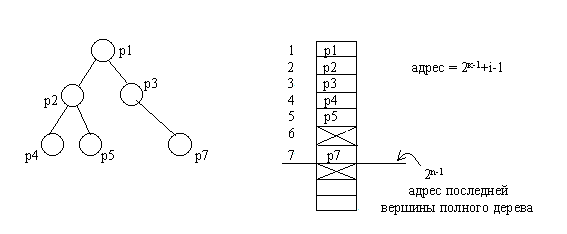
Адрес любой вершины в массиве = 2k-1+ i — 1, где k – номер уровня узла (вершины), i – номер на уровне k в полном бинарном дереве.
Адрес корня считается равным единице.
Основным недостатком представления бинарного дерева в виде массива как статической структуры является то, что размер массива выбирается, исходя из максимально возможного количества уровней бинарного дерева; причем, чем менее полным является дерево, тем менее рационально используется память.
Естественно, использование динамического массива для представления бинарного дерева будет более рационально.
Списочное представление бинарных деревьев
Для бинарных деревьев удобной реализацией является динамическая списковая структура, состоящая из элементов, соответствующих узлам дерева. Каждый элемент представляется записью, которая имеет одно или несколько полей данных и два поля указателей, один из которых используется для связывания элемента с правым потомком, а другой – с левым; листья имеют пустые указатели на потомков.
На самом деле, этот способ представления бинарного дерева является разновидностью мультисписка, образованного комбинацией множества линейных списков: каждый линейный список объединяет узлы, входящие в путь от корня дерева к одному из листьев.
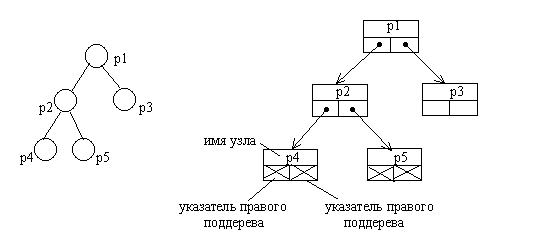
Объявление элементов бинарного дерева
type
tree = ^node;
node = record
data : char;
left, right : tree;
end;
При таком способе представления дерева следует сохранять в некоторой переменной указатель на узел, являющийся корнем дерева:
var
Root: tree;
Основные операции с деревом (построение, обход, поиск вершин по некоторому условию и др.) реализуются рекурсивными алгоритмами, так как дерево представляет собой рекурсивную структуру данных: каждое поддерево тоже является деревом.
Прохождение бинарных деревьев
Для выполнения определённой операции с каждым элементом дерева необходимо получить доступ к каждому узлу дерева, т. е. выполнить обход дерева, при котором его узлы посещаются по одному разу в определенном порядке.
Прямой порядок прохождения бинарного дерева (обход сверху вниз) можно определить следующим описательным рекурсивным алгоритмом:
попасть в корень;
обойти в прямом порядке (от предка к потомку до листьев) левое поддерево;
обойти в прямом порядке правое поддерево.
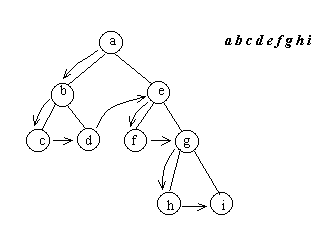
Рекурсивная процедура добавления последовательно по одному узлу в прямом порядке:
procedure Create(var p: tree); { указатель на созданную вершину – выходной параметр процедуры }
var
c: char;
begin
read(c);
if c <> ’.’ then
begin
new(p);
p^.data:= c;
Create( p^.left); { рекурсивный вызов по левой ветви }
Create( p^.right); { рекурсивный вызов по правой ветви }
end
else
p:= Nil;
end;
Для построения всего дерева обращение к данной процедуре Create должно происходить только один раз в главной программе или другом вызывающем модуле:
Create(Root);
Прохождение бинарного дерева в обратном порядке (обход снизу вверх) можно определить таким описательным рекурсивным алгоритмом
пройти в обратном порядке (от листьев к узлу, от потомка к предку) левое поддерево;
пройти в обратном порядке правое поддерево;
попасть в корень.
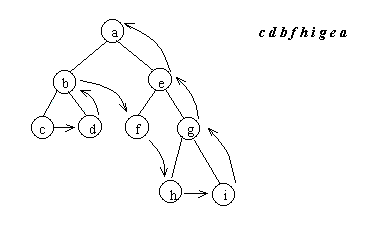
Симметричный порядок прохождения бинарного дерева (обход слева направо) определяется следующим описательным рекурсивным алгоритмом:
пройти в симметричном порядке (от листа к узлу, от узла к листу) левое поддерево;
попасть в корень;
пройти в симметричном порядке правое поддерево.
