2.3. Расчеты

2.3.1. Расчет основных элементов и устройств датчика

Расчеты и выбор оптимальных параметров датчиков, предназначенных для различных диапазонов, выполняются с помощью САПР. Конструкция датчика, используемая технология изготовления чувствительного элемента и структура кристалла варьируются в зависимости от требований к качеству этих датчиков, то есть конкретные данные по чувствительности, нелинейности, степени перегрузки задаются САПР, которая проектирует по этим данным датчик.

1) Расчет параметров деформационного чувствительного элемента (мембраны)

Исходные данные:

1. Максимальное значение измеряемого давления ……………….9332,54Па;

2. Минимальное значение измеряемого давления ………………..1333,22Па;

3. Максимальный радиус мембраны R………………………………….…20·10^-3м;

4. Плотность кремния ρ………………………………………………….2,32·10⁶Па;

5. Модуль продольной упругости Е…………………………………...1.,87·10¹¹Па;

6. Коэффициент Пуассона μ…………………………………………………...0,358;

7. Предельно допустимое напряжение σ_в……………………………….100·10⁶Па;

8. Принятое значение деформации Δl……………………………………..0,6·10^-6м;

9. Рекомендуемое соотношение …………………………………………...…≥25.

I. Прогиб центра мембраны при жесткой заделке и отсутствии первоначального натяга определяют по формуле [2.23] :

, (2.43)

где Δ – прогиб центра мембраны, м; р – давление, Н/м²; R – эффективный радиус мембраны, м; μ – коэффициент Пуассона; Е – модуль продольной упругости, Н/м²; h – толщина, м.

Из этой зависимости можно найти максимальный прогиб мембраны Δ в ее центре:

, (2.44)

Независимо от способа заделки и типа плоские тонкие металлические, кварцевые и сапфировые мембраны имеют линейную зависимость напряжений от действующего распределенного давления при прогибе давления их центров, не превышающем 1/3 толщины. При этом нелинейность характеристик упругих плоских мембран не превышает 5-6%.

Если по условиям эксплуатации допустимые нелинейность и гистерезис датчиков должны быть не более 1,5%, то необходимо обеспечить условие, при котором прогиб центра мембраны не должен превышать 1/10 ее толщины. Под плоской мембраной понимают мембрану, в которой .

Рис.2.20. Схема мембраны

При заданных габаритах датчика принимаем из конструктивных соображений: D=40мм; h=0,5мм. Остальные данные, входящие в зависимость (2), принимаем из исходных данных, приведенных выше.

Методика расчета заимствована из []Осиповича. Расчет проведем в следующей последовательности:

1. Определяем прогиб мембраны:

при условии:

2. Проведем расчеты радиальных σ_r, тангенсальных σ_t, эквивалентных σ_э напряжений для построения эпюры их распределения на мембране.

2.1. Определяем радиальные напряжения в различных точках мембраны из соотношения:

, (2.45)

где σ_r – напряжение в радиальном сечении, Па; h – толщина мембраны; р – распределенное давление на мембране, Па; R – радиус мембраны в заделке, м; r_i – текущее значение радиуса, м; μ – коэффициент Пуассона.

При r₁ = -20·10^-3м :

При r₂ = -1810^-3м ;

при r₃ = -1610^-3м ;

при r₄ = -1410^-3м ;

при r₅ = -1210^-3м ;

при r₆ = -1010^-3м ;

при r₇ = -810^-3м ;

при r₈ = -610^-3м ;

при r₉ = -410^-3м ;

при r₁₀ = -210^-3м ;

при r₁₁ = 0м ;

при r₁₂ = 210^-3м ;

при r₁₃ = 410^-3м ;

при r₁₄ = 610^-3м ;

при r₁₅ = 810^-3м ;

при r₁₆ = 10 10^-3м ;

при r₁₇ = 1210^-3м ;

при r₁₈ = 1410^-3м ;

при r₁₉ = 1610^-3м ;

при r₂₀ = -1810^-3м ;

при r₂₁ = -2010^-3м .

На рис.2.21. показано распределение радиального напряжения на мембране.

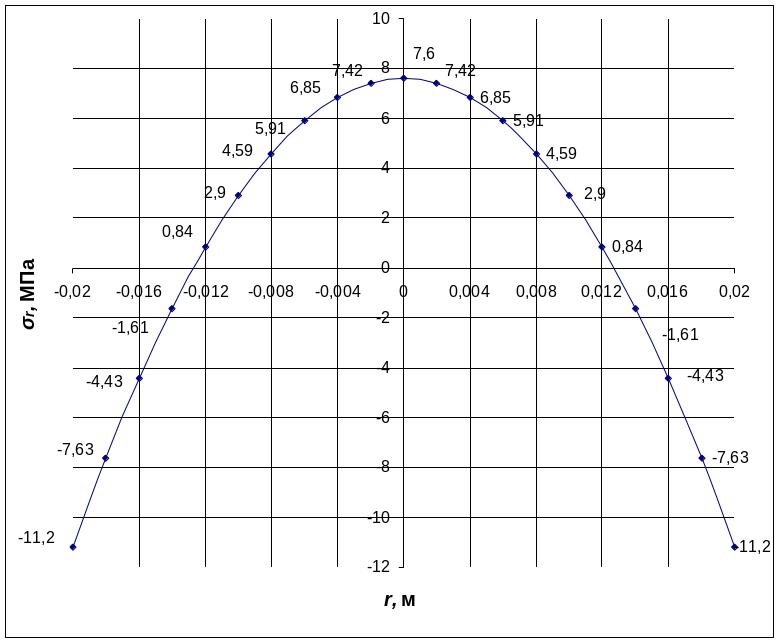
Рис.2.21. Распределение радиального напряжения на мембране

2.2.Определяем тангенциальные напряжения в различных точках мембраны:

(2.46)

При r₁ = -2010^-3м:

При r₂ = -1810^-3м ;

при r₃ = -1610^-3м ;

при r₄ = -1410^-3м ;

при r₅ = -1210^-3м ;

при r₆ = -1010^-3м ;

при r₇ = -810^-3м ;

при r₈ = -610^-3м ;

при r₉ = -410^-3м ;

при r₁₀ = -210^-3м ;

при r₁₁ = 0м ;

при r₁₂ = 210^-3м ;

при r₁₃ = 410^-3м ;

при r₁₄ = 610^-3м ;

при r₁₅ = 810^-3м ;

при r₁₆ = 10 10^-3м ;

при r₁₇ = 1210^-3м ;

при r₁₈ = 1410^-3м ;

при r₁₉ = 1610^-3м ;

при r₂₀ = -1810^-3м ;

при r₂₁ = -2010^-3м .

На рис.2.22 показано распределение тангенциального напряжения на мембране.

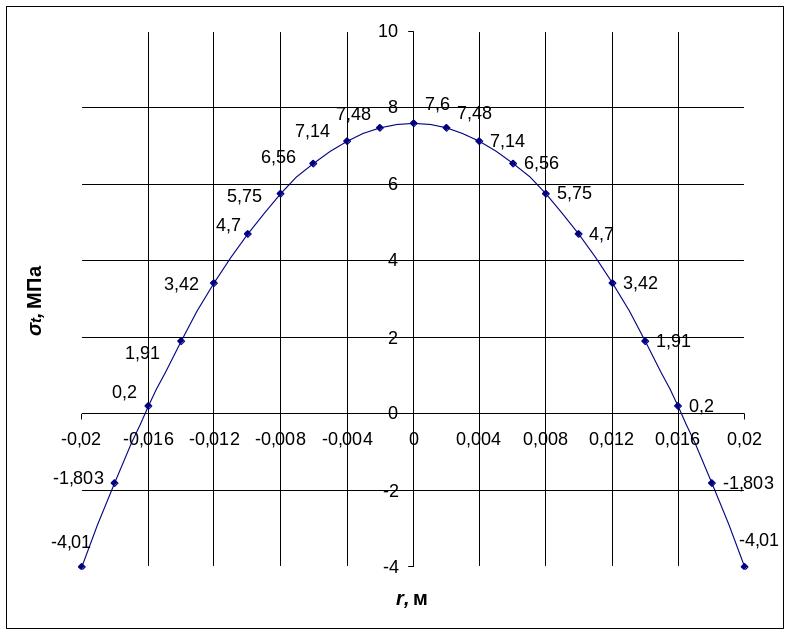
Рис.2.22. Распределение тангенциального напряжения на мембране

2.3. Определяем величину эквивалентных напряжений по формуле:

. (2.47)

Подставив значения в выражение (2.47) получим:

При r₁ = -2010^-3м:

При r₂ = -1810^-3м ;

при r₃ = -1610^-3м ;

при r₄ = -1410^-3м ;

при r₅ = -1210^-3м ;

при r₆ = -1010^-3м ;

при r₇ = -810^-3м ;

при r₈ = -610^-3м ;

при r₉ = -410^-3м ;

при r₁₀ = -210^-3м ;

при r₁₁ = 0м ;

при r₁₂ = 210^-3м ;

при r₁₃ = 410^-3м ;

при r₁₄= 610^-3м ;

при r₁₅ = 810^-3м ;

при r₁₆ = 10 10^-3м .

при r₁₇ = -1210^-3м ;

при r₁₈ = -1410^-3м ;

при r₁₉ = -1610^-3м ;

при r₂₀ = -1810^-3м ;

при r₂₁ = -2010^-3м ;

На рис.2.23 показано распределение эквивалентного напряжения на мембране.

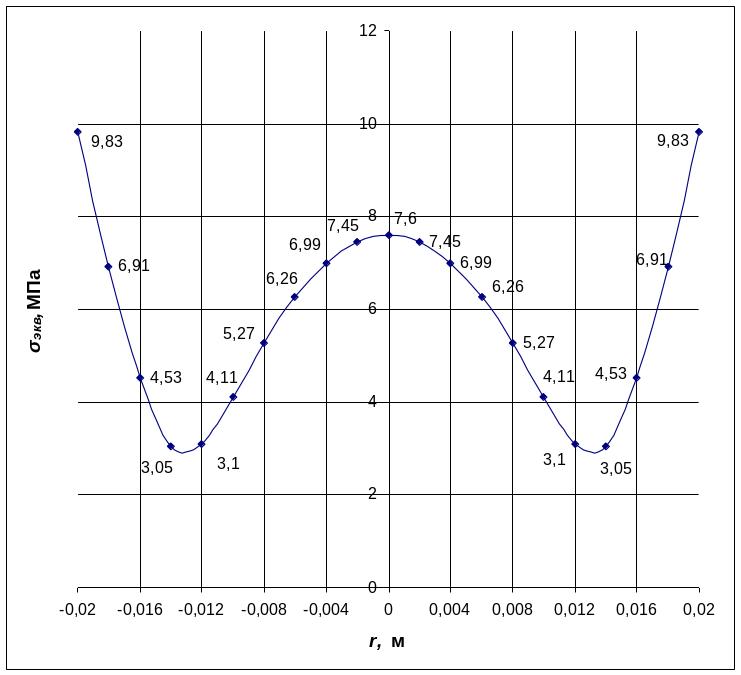
Рис.2.23. Распределение эквивалентного напряжения на мембране

3. Проверим мембрану на прочность из условия:

, (2.48)

где [] ≈ _в /2 – допустимое напряжение;  _в =100·10⁶ Па.

Так как, напряжения, действующие на мембрану, не выходят за пределы допустимого значения,  _экв = 9,8310⁶ Па  [50 10⁶ Па] следовательно, можно окончательно принять толщину мембраны h 0,510^-3 м 0,5мм.

На основе анализа полученных эпюр радиальных _r и тангенциальных _t напряжений, а так же с учетом эпюры эквивалентных напряжений  _экв определили, что тело тензорезистора должно находится на участке мембраны с минимальных градиентом напряжений, то есть выбираем длину тензорезистора l = 3мм, а его расположение на мембране с радиусом r _min = 1мм. Размещение тензорезисторов на мембране показано на рис.2.24.

Рис.2.24. Топология тензорезисторов на мембране

Размещение измерительного тензорезистора на мембране за пределами выбранного радиуса приведет к его работе в условиях значительного градиента напряжений, и, следовательно, к быстрому его разрушению.

4. Средняя относительная деформация мембраны на участке напыления тензорезисторов:

а) центрального

; ;

, (2.49)

где l_д – длина датчика (база), мм; где h – толщина мембраны; р – распределенное давление на мембране, Па; R – текущее значение радиуса, м; μ – коэффициент Пуассона; Е – модуль продольной упругости; r₁=1мм и r₂=4мм –соответствующие радиусы см. рис.2.24.

.

б) периферийного

; ;

Для расчета используем формулу (9), где =15мм и =18мм - соответствующие радиусы см. рис.2.24.

5. Изменения сопротивлений тензорезисторов определяют по формулам:

а) центрального

, (2.50)

где =1-коэффициент снижения передачи деформации тензорезистору; ; R₀=750Ом; =0,00247- средняя относительная деформация мембраны на участке напыления тензорезисторов.

б) периферийного

(2.51)

где =1- коэффициент снижения передачи деформации тензорезистору; ; R₀=750Ом; = - 0,0027 - средняя относительная деформация мембраны на участке напыления тензорезисторов.

.

6. Суммарное изменение сопротивления определяется:

, (2.51)

где - изменение сопротивления центрального тензорезистора; - изменение сопротивления периферийного тензорезистора.

II. Расчет частотной характеристики датчика, мембрана которого соприкасается с жидкостью.

Собственная частота незатухающих колебаний датчика, заполненного жидкостью и снабженного абсолютно жесткими трубопроводами или катетерами, определяют по формуле:

(2.53)

где R=0,002м- внутренний радиус катетера; Е_V – модуль объемной упругости, Н·м^-5; l=0,015м – длина катетера; ρ =1030 кг/м³– плотность среды (физраствора).

Одной из основных характеристик, определяющих частотные свойства датчика, заполненного жидкостью, является модуль объемной упругости Е_V:

, (2.54)

где р – распределенное давление, Па; ΔV – увеличение объема рабочей камеры датчика при давлении р_ном, м³.

Приращение объема ΔV для датчиков с плоскими мембранами, жестко заделанными в корпус, определяют по формуле:

, мм³, (2.55)

где R – эффективный радиус мембраны, мм ; z – параметр, при Δ<h z=3. Так как , h=0,5мм 0,01мм<0,5мм z=3.

Приращение объема ΔV составит:

.

Модуль объемной упругости Е_V составит:

.

Собственная частота незатухающих колебаний датчика составит (см.(2.53)):