3º. Теорема о сложении скоростей

Теорема (о сложении скоростей)

Абсолютная скорость точки в сложном движении равна сумме переносной скорости точки и ее относительной скорости, т.е. справедливо равенство

. (4.2.12)

Доказательство

Положение точки  в абсолютном пространстве в момент времени можем представить в виде суммы (см. рис. 4.2.1):

, (4.2.13)

где

• — положение в абсолютном пространстве полюса подвижной системы , задаваемое в момент времени проекциями на неподвижные оси;

• — положение точки в момент времени относительно полюса , задаваемое проекциями на подвижные оси.

Разложение вектора по подвижному базису  в любой момент времени  совпадает с разложением вектор-функции , задающей относительное движение точки.

Так что согласно (4.1.6) из §1 можем записать:

.

Дифференцируем равенство (4.2.13)

(4.2.13)

по времени  :

.

Согласно (4.1.6) из §1 вектор-функция задается в проекциях на подвижные оси, так как .

Рис. 4.2.1

Применяя к вектору  формулу (4.2.11)

, (4.2.11)

получим

. (4.2.14)

В правой части этого равенства имеем:

• в соответствии с определением 1 из §2, — это абсолютная скорость точки (полюса подвижной системы);

• в соответствии с определением 2 из §2, 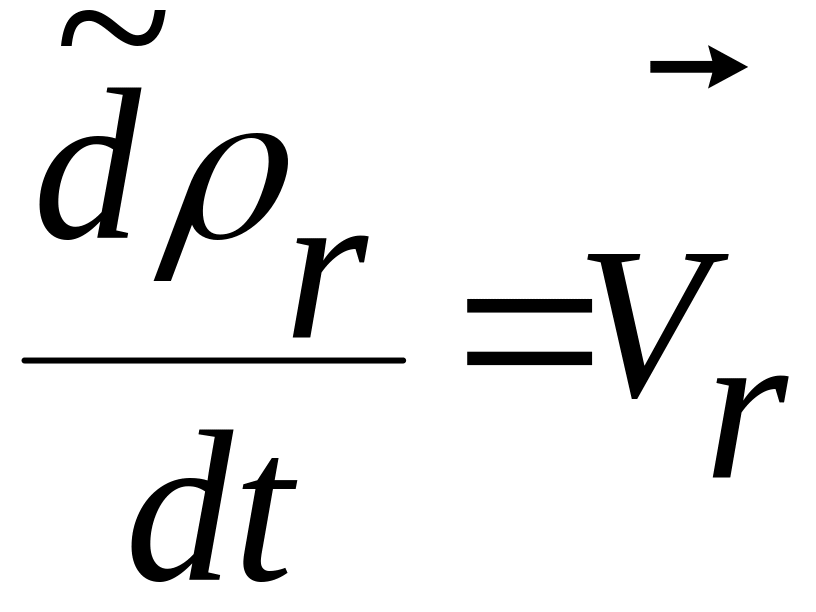— относительная скорость точки ;

• согласно формуле (4.2.8), — переносная скорость точки  .

Заменяя в правой части (4.2.14) указанные выражения на   и  , придем к равенству (4.2.12)

. (4.2.12)

Теорема доказана.